Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Composition of Velocities in Perpendicular Directions
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we'll start by learning about how to find the resultant velocity when two velocities act at right angles to each other. Can anyone tell me what formula we might use?
Is it the Pythagorean theorem?
Exactly! We use \( v_R = \sqrt{v_1^2 + v_2^2} \) where \( v_R \) is the resultant velocity. Let's use an example: a bird flying at 50 m/s east and 60 m/s north. What would the resultant velocity be?
I think it's \( \sqrt{(50)^2 + (60)^2} \) which equals 78.10 m/s.
Perfect! And now, how about the direction?
We would use \( \theta = \tan^{-1}(60/50) \), so it's approximately 50.19 degrees north of east.
Great work, everyone! Let's summarize the key points: we find the resultant velocity using the Pythagorean theorem and the direction using tangent.
Resolution of Velocity
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's shift gears and talk about resolving velocity. Who can explain what we mean by 'resolving' a velocity vector?
It's breaking down a velocity into its components, usually horizontal and vertical.
Exactly! For example, if a plane flies at 200 m/s at an angle of 40 degrees to the horizontal, how do we find its components?
We can use trigonometric functions: \( v_x = v \cos(\theta) \) and \( v_y = v \sin(\theta) \).
That's right! So for our plane, what do we get for each component?
The horizontal component \( v_x \) is about 153.2 m/s and \( v_y \) is about 128.6 m/s.
Fantastic! Remember, this resolution helps us analyze the motion of objects more easily. Let's recap: we resolve velocity using cosine and sine based on the angle given.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
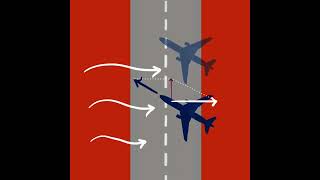
In this section, we explore numerical problems involving the composition and resolution of velocities, detailing how to calculate resultant velocities when velocities are acting perpendicular to each other and how to resolve them into horizontal and vertical components.
Detailed
In this section, we delve into numerical problems involving the composition and resolution of velocities. Composition of velocities involves calculating the resultant velocity when two vectors act at right angles to one another. For instance, if a bird is flying with velocities of 50 m/s eastward and 60 m/s northward, to find the resultant velocity, we apply the Pythagorean theorem. Here, the resultant velocity is calculated as: \( v_R = \sqrt{(50)^2 + (60)^2} = \sqrt{6100} \approx 78.10 \, ext{m/s} \), and the direction is given by \( \theta = \tan^{-1}(\frac{60}{50}) \approx 50.19^{\circ} \) north of east. Resolution of velocity involves breaking down a single vector into its components; for instance, when a plane flies at 200 m/s at an angle of 40Β° to the horizontal, its components can be found using trigonometric functions, resulting in approximately 153.2 m/s horizontally and 128.6 m/s vertically. This section emphasizes the importance of these calculations in real-world applications, enhancing our understanding of the motion of objects.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Example 2: Resolution of Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A plane is flying at 200 m/s at an angle of 40Β° to the horizontal. Find the horizontal and vertical components of its velocity.
Solution:
v_x=200cos (40Β°)=200Γ0.7660β153.2 m/s
v_y=200sin (40Β°)=200Γ0.6428β128.6 m/s
The horizontal component of velocity is approximately 153.2 m/s, and the vertical component is approximately 128.6 m/s.
Detailed Explanation
In this example, a plane is flying at a certain speed (200 m/s) at a specific angle (40Β°) to the horizontal. To break this velocity down into its horizontal (x) and vertical (y) components, we use trigonometry.
- The horizontal component (v_x) can be found using the cosine function:
- v_x = 200 * cos(40Β°) = 200 * 0.7660 β 153.2 m/s.
- The vertical component (v_y) is found using the sine function:
- v_y = 200 * sin(40Β°) = 200 * 0.6428 β 128.6 m/s.
The reason we split the velocity this way is to understand how much of the plane's motion is directed straight up (vertical component) compared to how much is moving forward (horizontal component).
Examples & Analogies
Think of riding a bicycle uphill at an angle. If you're going forward fast, part of your speed is directed up the hill (the vertical direction), and part is going straight ahead along the path (the horizontal direction). Using some math, we can find out how much of your speed is contributing to climbing up and how much is just making you zoom along the bike path. This helps us understand your actual movement on the incline!
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Resultant Velocity: The combined effect of two or more velocities acting simultaneously.
-
Composition of Velocity: Process of adding vectors to determine a single resultant vector.
-
Resolution of Velocity: Breaking down a vector into perpendicular components to simplify calculations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A bird is flying with a velocity of 50 m/s east and 60 m/s north; the resultant velocity is approximately 78.10 m/s at an angle of 50.19Β° north of east.
-
A plane flying at 200 m/s at an angle of 40Β° has horizontal and vertical components of approximately 153.2 m/s and 128.6 m/s respectively.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
To find the total speed, see the vectors play, Pythagorean square, then the angles sway.
π Fascinating Stories
-
Imagine a bird flying diagonally; it constantly struggles to find its way. One day, realizing it must choose directions, it combines its speed in both ways to see where it lands!
π§ Other Memory Gems
-
R&R: Remember to Resolve and then find Resultant!
π― Super Acronyms
C.R.E.W.
- Composition
- Resolution
- Example
- Working together.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Resultant Velocity
Definition:
The overall velocity of an object resulting from the vector addition of two or more velocities.
-
Term: Composition of Velocity
Definition:
The process of combining two or more velocities acting in different directions to determine the resultant velocity.
-
Term: Resolution of Velocity
Definition:
The process of breaking down a single velocity vector into its components along different directions.
-
Term: Pythagorean Theorem
Definition:
A mathematical formula used to find the length of a side in a right triangle, given by \( a^2 + b^2 = c^2 \).