Diagonalization and Matrix Powers
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Diagonalization
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's start with diagonalization. When we have a square matrix A, it can be diagonalized if we can express it as A = PDP^(-1), where D is a diagonal matrix.

What does that diagonal matrix D represent exactly?

Great question! The matrix D contains the eigenvalues of A along its diagonal. That means each diagonal entry corresponds to how A behaves in different 'directions'.

So if we know the eigenvalues, we can simplify calculations?

Exactly! Once A is in diagonal form, operations like raising A to a power become straightforward. Instead of calculating A^k directly, we can compute it as A^k = PD^kP^(-1), simplifying our work significantly.

Can you explain what D^k looks like?

Certainly! D^k is simply the diagonal matrix where each eigenvalue is raised to the power k. For example, if D = diag(λ1, λ2, ...), then D^k = diag(λ1^k, λ2^k, ...).

This seems really useful in engineering!

Absolutely, especially in civil engineering where analyzing structures efficiently is key. Summary: Diagonalization changes complexity into simplicity, especially when computing matrix powers.
Applications in Civil Engineering
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s connect diagonalization to civil engineering. In structural analysis, how do you think diagonalizing matrices helps?

Maybe it helps in analyzing vibrations in structures?

Spot on! Eigenvalues derived from the stiffness matrix tell us about the natural frequencies of the structure. Each eigenvector corresponds to a 'mode shape' — how the structure moves at these frequencies.

What about dynamic systems?

Good point! In dynamic systems, diagonalization allows us to break down complex multi-degree-of-freedom systems into simpler single-degree systems, making simulations faster.

Is there a specific field within civil engineering where this is most vital?

Yes, particularly in earthquake engineering. Understanding how structures respond and vibrate during seismic events relies heavily on these concepts.

That’s fascinating! So diagonalization is crucial for safety in architecture.

Exactly! Recap: Diagonalization is vital in civil engineering, especially for structural analysis and dynamics.
Computational Efficiency
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s discuss computational efficiency next. Why do you think it's important to be able to raise matrices to powers quickly?

It saves time, especially with large matrices!

Exactly! High-dimensional matrices can be computationally intensive. Diagonalization simplifies this by reducing operations to diagonal forms, which are much easier.

Are there specific software tools that help with this?

Yes! Tools like MATLAB and Python's NumPy simplify diagonalization and allow engineers to compute eigenvalues and eigenvectors efficiently. Knowing commands can help a lot.

Can you summarize that?

Sure! Diagonalization breaks complicated computations into simpler diagonal tasks, especially useful in simulations for engineering applications.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section discusses how diagonalization simplifies the computation of matrix powers, allowing for quick transformations in dynamic systems and simulations. It details the relationship between a matrix and its diagonal form, emphasizing practical applications in civil engineering.
Detailed
Diagonalization and Matrix Powers
Diagonalization is a powerful concept that enables the simplification of matrix operations. When a square matrix A is diagonalized as A = PDP^(-1), where D is a diagonal matrix composed of A's eigenvalues, it transforms raising A to powers into a much simpler operation. Specifically, for any positive integer k, the power of A can be computed efficiently as A^k = PD^kP^(-1). The diagonal matrix D^k consists of the eigenvalues raised to the power k, making computations straightforward, especially for repeated transformations, dynamic systems, and state-transition models.
This method is particularly relevant in civil engineering applications, such as when analyzing vibrational systems and designing structures, where efficiency in calculations is crucial. Diagonalization allows engineers to decouple complex matrices into independent components, each corresponding to a mode of vibration or natural frequency, significantly simplifying the analysis and computation necessary for designing sturdy systems.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Key Application of Diagonalization
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
One of the major applications of diagonalization is computing matrix powers efficiently:
Detailed Explanation
The process of diagonalization allows us to rewrite any square matrix in a form that is simpler to work with. Specifically, when we diagonalize a matrix A, we express it in the form A = PDP⁻¹, where D is a diagonal matrix. This transformation simplifies the calculation of powers of the matrix, such as A^k. Instead of multiplying the matrix A by itself k times, we can instead raise the diagonal matrix D directly to the power k, which is computationally easier and faster.
Examples & Analogies
Think of diagonalization like a shortcut in a calculator app that allows you to quickly compute powers of numbers. Instead of calculating 2^10 by multiplying 2 by itself ten times, you could use a 'power' function that instantly computes powers with a single button press. In engineering, this saves significant time in simulations that involve complex system interactions.
Raising Diagonal Entries to Powers
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
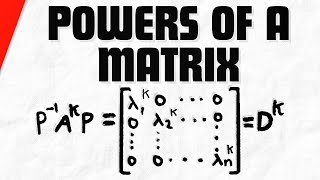
Let: A=PDP−1⇒Ak =PDkP−1 Where Dk is just the diagonal matrix with each diagonal entry raised to the power k:
Detailed Explanation
In the context of the diagonal matrix D, when we calculate D^k, we raise each entry on the diagonal to the power k. This is straightforward: if D has diagonal entries λ1, λ2, ..., λn, then D^k has diagonal entries λ1^k, λ2^k, ..., λn^k. This significant simplification means that instead of working with the full matrix, we only need to focus on the diagonal elements, which makes calculations in engineering applications much simpler and faster.
Examples & Analogies
Consider a situation where you need to track the growth of a bank account with different interest rates over several years. Instead of recalculating the total amount directly for each year with complex formulas for multiple accounts, if you simplified your calculations to just focus on the interest rates (like the diagonal entries), you could quickly compute projected values using powers—each account's growth can be managed straightforwardly. This analogy shows how breaking down the problem simplifies our overall computations.
Efficiency in Simulations
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This is computationally much faster and accurate in simulations involving repeated transformations, dynamic systems, and state-transition models.
Detailed Explanation
When engineers design systems—like buildings or bridges—they often have to model how these structures respond over time under various loads and conditions. Utilizing diagonalization means they can efficiently compute transformations that correspond to how the system evolves, leading to faster simulations. This efficiency is crucial, as engineers often deal with complex systems where quick calculations can significantly affect analysis and design decisions.
Examples & Analogies
Imagine you are running a race where you have to calculate your time at various checkpoints. If you can quickly determine your expected time based on patterns you've observed in past races—you can optimize your pacing without constantly recalculating your exact position. This is akin to using diagonalization in dynamic system simulations, where quick calculations lead to better planning and outcomes.
Key Concepts
-
Diagonalization: A method to express a matrix as a product of a diagonal matrix and invertible matrix.
-
Matrix Powers: The operation of raising a matrix to an integer power, simplified by diagonalization.
-
Eigenvalues and Eigenvectors: Fundamental components in the process of diagonalization, revealing the characteristics of the matrix.
Examples & Applications
To compute A^3 for a diagonal matrix D = diag(λ1, λ2), simply compute D^3 = diag(λ1^3, λ2^3).
In civil engineering, the eigenvalues obtained from the stiffness matrix help predict how structures will respond to forces.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When the matrix is neat, and eigenvalues greet, diagonalize, and calculate with speed!
Stories
Imagine a matrix that was too tough to crack. With diagonalization, it became a smooth track—computing its powers without a hitch!
Memory Tools
To remember diagonalization: 'Powers Done Simply (PDS)' — it emphasizes the simplification process.
Acronyms
D.E.C.O
Diagonalization Enables Computational Optimization.
Flash Cards
Glossary
- Diagonal Matrix
A matrix in which all the entries outside the main diagonal are zero.
- Eigenvalue
A scalar associated with a linear transformation of a vector space that measures the factor by which the eigenvector is stretched or shrunk.
- Eigenvector
A non-zero vector that only changes by a scalar factor when a linear transformation is applied.
- Similarity Transformation
A transformation that changes a matrix into a similar matrix, usually by the process of diagonalization.
- Natural Frequency
The frequency at which a system naturally oscillates when not subjected to external forces.
Reference links
Supplementary resources to enhance your learning experience.
