Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Characteristic Polynomial and Eigenvalues
Unlock Audio Lesson
Today, we’ll begin to discuss how to diagonalize a matrix by starting with the characteristic polynomial. Can anyone remind us what the characteristic polynomial is?
It's the determinant of A minus λ times the identity matrix, right?
Exactly! We express it as det(A - λI) = 0. What do we find when we solve this equation?
We find the eigenvalues of the matrix!
Correct! Eigenvalues are the solutions (λ1, λ2, ..., λn). Moving forward, what’s the next step after we have our eigenvalues?
We need to find the eigenvectors corresponding to each eigenvalue.
Great! This will involve solving the equation (A - λiI)v = 0 to find the null space for each λi. Let’s keep this in mind as we move forward.
Finding Eigenvectors
Unlock Audio Lesson
Now that we know how to find eigenvalues, let’s explore how to determine the eigenvectors. Why do we need to find these?
Because they help us construct the matrix that will be crucial for diagonalization!
Exactly right! Eigenvectors provide us the columns for matrix P. Can anyone explain why they need to be linearly independent?
If the eigenvectors are not linearly independent, then our matrix P won't be invertible, which is needed to validate our diagonalization.
Spot on! Remember, the diagonalization process hinges upon the invertibility of P. The final step we discussed earlier involves forming matrix P with these eigenvectors.
Constructing Matrix D and Finalizing Diagonalization
Unlock Audio Lesson
As we get closer to our final product of diagonalization, can someone summarize how we construct our diagonal matrix D?
The diagonal matrix D contains the eigenvalues along its diagonal, right?
Exactly! D has the structure of λ1 in (1,1), λ2 in (2,2), and so forth. What’s the last check we need to perform before we conclude the diagonalization?
We need to ensure that our matrix P is invertible to express A as A = PDP−1.
Correct! With that, we have followed through the complete diagonalization process, enabling us to easily compute powers of A with Ak = PDkP−1. Well done!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section outlines a systematic method for diagonalizing a square matrix, explaining the relationship between eigenvalues, eigenvectors, and the construction of matrices that facilitate easier computation. The outlined steps are essential for simplifying complex matrix operations, particularly relevant to applications in engineering.
Detailed
Detailed Summary
Diagonalization is crucial in linear algebra, particularly within civil engineering applications like structural analysis and systems of differential equations. In this section, we detail the step-by-step procedure to diagonalize a matrix A:
- Find the Characteristic Polynomial: We start by calculating the determinant (det(A - λI) = 0) to find the characteristic polynomial.
- Determine Eigenvalues: The roots of this polynomial give us the eigenvalues (λ1, λ2, ... , λn).
- Find Eigenvectors: For each eigenvalue λi, we discover its corresponding eigenvectors by solving the null space equation ((A - λiI)v = 0).
- Construct Matrix P: We then form matrix P using the linearly independent eigenvectors as columns.
- Form Diagonal Matrix D: Finally, we create diagonal matrix D which contains the eigenvalues.
- Check Invertibility: It’s essential to ensure that P is invertible. We can then express the original matrix as A = PDP−1.
Through this process, engineers can greatly simplify calculations involving matrix operations, thereby providing a more efficient pathway to solving complex problems.
Youtube Videos
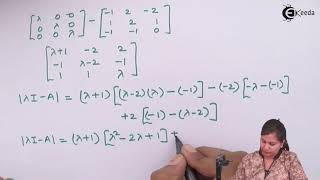
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Step 1: Find the Characteristic Polynomial
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Given a square matrix A, follow these steps:
Step 1: Find the characteristic polynomial:
det(A−λI)=0
Detailed Explanation
The first step in diagonalizing a matrix is to calculate its characteristic polynomial. The characteristic polynomial is found by taking the determinant of the matrix (A − λI), where λ is a scalar (the eigenvalue), and I is the identity matrix of the same size as A. Setting this determinant to zero gives us a polynomial equation that can be analyzed to find the eigenvalues of the matrix.
Examples & Analogies
Think of this step like finding the roots of a polynomial function. Just like how finding the roots allows you to understand the behavior of that polynomial, finding the eigenvalues helps us understand the behavior of the matrix in linear transformations.
Step 2: Find All Eigenvalues
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Step 2: Find all eigenvalues λ₁, λ₂, ..., λₙ.
Detailed Explanation
In this step, you solve the characteristic polynomial equation obtained in Step 1 to find the eigenvalues of the matrix A. The solutions to this equation are the eigenvalues (λ), which are critical for the diagonalization process. Eigenvalues are important because they provide insights into the properties of the matrix, such as stability and oscillatory behavior in engineering applications.
Examples & Analogies
Finding eigenvalues is akin to determining the frequencies of musical notes when you pluck a string. Each note's frequency corresponds to a specific eigenvalue, revealing the underlying structure of the musical piece, just like eigenvalues reveal characteristics of the matrix.
Step 3: Find Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Step 3: For each eigenvalue λᵢ, find the null space of (A−λᵢI) to get the corresponding eigenvectors.
Detailed Explanation
Once the eigenvalues have been determined, the next step is to find the eigenvectors associated with each eigenvalue. This involves solving the equation (A−λᵢI)v = 0 for each eigenvalue λᵢ. The solutions to this equation, if linearly independent, form the eigenvectors, which are crucial for constructing the diagonalizing matrix P.
Examples & Analogies
Imagine eigenvectors like the paths a ball could take after being kicked in different directions. Each direction (eigenvector) corresponds to a specific force (eigenvalue) applied to the ball. Understanding these paths helps us predict where the ball will go.
Step 4: Form Matrix P
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Step 4: Form matrix P using linearly independent eigenvectors as columns.
Detailed Explanation
In this step, you compile the linearly independent eigenvectors obtained from Step 3 into a new matrix P. Each column of P represents an eigenvector of the matrix A. This matrix P is critical for the diagonalization process, as it will be used to transform the original matrix A into the diagonal matrix D.
Examples & Analogies
Think of matrix P as a team working together to achieve a goal. Each member (eigenvector) has their unique strengths, and together, they create a well-structured unit (matrix) that can effectively tackle complex tasks (matrix transformations).
Step 5: Construct Diagonal Matrix D
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Step 5: Construct diagonal matrix D with eigenvalues λ₁, λ₂, …, λₙ along the diagonal.
Detailed Explanation
This step involves creating a diagonal matrix D in which the entries along the diagonal are the eigenvalues found in Step 2. The diagonal matrix D represents the simplified version of the matrix A, making subsequent calculations, such as matrix powers, much easier.
Examples & Analogies
Imagine creating a simplified summary of complex data. The diagonal matrix D is like that summary—it distills the essential information (eigenvalues) from the more complex structure (original matrix A), allowing for quicker insights and calculations.
Step 6: Check Invertibility of P
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Step 6: Check the invertibility of P and compute P⁻¹. Then, A=PDP⁻¹.
Detailed Explanation
The final step in the diagonalization process is to confirm that the matrix P is invertible. This is essential for the diagonalization to be valid. If P is invertible, you can compute its inverse P⁻¹ and then express the original matrix A in the form A = PDP⁻¹. This relationship shows that A is similar to the diagonal matrix D, allowing for simpler matrix computations.
Examples & Analogies
This step is akin to verifying that the replacement of ingredients in a recipe yields the same final dish. Just as you need to ensure you can substitute ingredients (invertibility), you must ensure that the transformation accurately represents the original dish (matrix).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Similarity Transformation: The process of converting a matrix into a simpler form using eigenvalues and eigenvectors.
-
Characteristic Equation: An equation derived from det(A - λI) = 0 used to find eigenvalues.
-
Invertibility: A matrix is invertible if it has a full set of linearly independent eigenvectors.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
To diagonalize matrix A = [[4, 1], [2, 3]], we determine the eigenvalues λ = 5 and 2 and form matrices P and D as described in the section.
-
If a matrix does not have enough eigenvectors, such as A = [[2, 1], [0, 2]], it cannot be diagonalized.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When you see a matrix to analyze, find eigenvalues to help you rise.
📖 Fascinating Stories
-
Imagine a wizard transforming a heavy spell into light by finding special magic numbers (eigenvalues) and charms (eigenvectors) that free each ingredient, making potions easy to brew - that’s diagonalization!
🧠 Other Memory Gems
-
Remember 'C E N D I' for steps: Characteristic polynomial, Eigenvalues, Null space for eigenvectors, D populations of matrix P, Invertibility check.
🎯 Super Acronyms
D.E.A.N. - Diagonalization involves **D**etermining eigenvalues, **E**igenvectors, **A**rranging into P and D, and **N**ormalizing through invertibility.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Diagonal Matrix
Definition:
A matrix where all off-diagonal elements are zero, facilitating simpler computations.
-
Term: Eigenvalue
Definition:
A scalar value that indicates how much an eigenvector is stretched or compressed during a linear transformation.
-
Term: Eigenvector
Definition:
A non-zero vector that, when multiplied by a matrix, yields a scalar multiple of itself, associated with its eigenvalue.
-
Term: Invertible Matrix
Definition:
A square matrix that has an inverse, meaning there exists another matrix that, when multiplied with it, yields the identity matrix.
-
Term: Characteristic Polynomial
Definition:
A polynomial whose roots are the eigenvalues of a matrix, given by the determinant equation det(A - λI) = 0.