Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Non-Diagonalizable Matrices
Unlock Audio Lesson
Today, we're focusing on non-diagonalizable matrices. Can anyone tell me what that means for a matrix?
It means the matrix doesn't have enough linearly independent eigenvectors, right?
Exactly! Without enough linearly independent eigenvectors, a matrix cannot be expressed in a diagonal form. This has significant implications in both theoretical and applied contexts.
So, what do we do with those matrices then?
Great question! We can use the Jordan form to analyze them. Think of the Jordan form as a bridge between diagonalization and analyzing non-diagonalizable matrices.
As a mnemonic, remember: 'Jumpy Jordan for stubborn matrices' – it helps to recall Jordan form is our go-to for these matrices.
So, it's like a second option when diagonalization fails?
Exactly! In many civil engineering applications, we find that the matrices we work with are well-behaved and can be diagonalized, making analysis simpler.
Implications of Non-Diagonalizability
Unlock Audio Lesson
Let's discuss the implications of having non-diagonalizable matrices. Why do you think it matters in civil engineering?
I guess it would make our calculations more complex?
Right! Non-diagonalizability can complicate numerical computations and system analyses. For example, higher-order differential equations can be harder to solve.
But you mentioned most matrices we deal with are diagonalizable?
Correct! Symmetric and well-structured matrices are often diagonalizable, making them easier to work with, especially in dynamic systems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Non-diagonalizable matrices lack enough independent eigenvectors for diagonalization. Despite this limitation, the Jordan canonical form provides an essential tool for analysis. In civil engineering, many relevant matrices are well-behaved and thus diagonalizable, ensuring simpler computations.
Detailed
In linear algebra, certain matrices cannot be diagonalized because they do not possess enough linearly independent eigenvectors, which is crucial for the diagonalization process. However, these matrices can still be effectively analyzed using the Jordan canonical form, a generalized approach to understanding matrix behavior. While Jordan form is useful for theoretical applications, it is worth noting that most physical systems in civil engineering typically yield symmetric or well-behaved matrices that are diagonalizable. This focus on diagonalizability simplifies many analytical operations, especially in dynamic modeling and structural analysis, making it a cornerstone concept in engineering applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Non-Diagonalizable Matrices
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Some matrices cannot be diagonalized because they don’t have enough linearly independent eigenvectors.
Detailed Explanation
Not all matrices can be simplified into diagonal form. A matrix is diagonalizable if it has enough linearly independent eigenvectors to create a complete basis. When a matrix lacks sufficient eigenvectors, it cannot be transformed into a diagonal matrix, which is required for easier computation in operations such as finding powers of the matrix.
Examples & Analogies
Think of it this way: if you're trying to build a square table but only have three legs, it becomes unstable. Similarly, a matrix may be 'unstable' or 'non-diagonalizable' if it lacks enough eigenvectors, meaning it can't be properly 'supported' for diagonalization.
Jordan Canonical Form
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Such matrices can still be analyzed using Jordan canonical form, which is a generalization of diagonalization.
Detailed Explanation
The Jordan canonical form allows for the study of matrices that are not diagonalizable. Essentially, it puts a matrix into a block form, where each block corresponds to an eigenvalue. This form captures some of the information that would be present in diagonalization but is designed for cases when a diagonal form is not achievable.
Examples & Analogies
Imagine a singer who can't hit all the notes perfectly but can still perform a song beautifully with some variations and adjustments. The Jordan form is like that adjustment, providing a way to understand the matrix's behavior even if it can't be neatly categorized into a diagonal form.
Matrices in Civil Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
However, for most physical systems modeled in civil engineering, matrices are usually symmetric or well-behaved, and thus diagonalizable.
Detailed Explanation
In civil engineering, the matrices arising from physical principles, such as those related to forces, displacements, and properties of materials, are often symmetric or have properties that ensure they are diagonalizable. This makes it far easier to analyze structures, predict their behavior, and perform necessary calculations.
Examples & Analogies
Think of engineers as chefs. When using fresh, high-quality ingredients (symmetric matrices), they can create beautiful and delicious dishes (predictable structural behaviors). However, if the ingredients are poor quality (non-diagonalizable matrices), it becomes challenging to achieve the desired results.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Non-Diagonalizable Matrices: Matrices that cannot be diagonalized due to lack of sufficient linearly independent eigenvectors.
-
Jordan Form: A special form of a matrix that allows for analysis even when diagonalization isn't possible.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
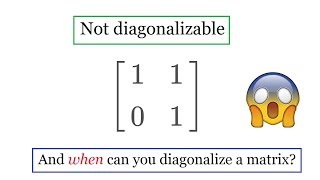
The matrix [2 1; 0 2] has an algebraic multiplicity of 2 for the eigenvalue 2, but only one linearly independent eigenvector, making it non-diagonalizable.
-
For physical structures analyzed using stiffness matrices, the matrices are typically diagonalizable, which simplifies the computation of natural frequencies.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
If lines are few, diagonalization won't do!
📖 Fascinating Stories
-
Imagine a detective (matrix) who can't find enough clues (independent eigenvectors) to solve a case (diagonalize the matrix). Instead, they keep a notebook (Jordan Form) to analyze the mystery!
🧠 Other Memory Gems
-
Remember JUMP for Jordan: Just Understand Matrices' Problems.
🎯 Super Acronyms
DIAMOND - Diagonalization Requires Independent And Multiple Eigenvectors Outwardly, Not Dimensional!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: NonDiagonalizable Matrix
Definition:
A matrix that cannot be expressed as a product of a diagonal matrix and an invertible matrix due to insufficient linearly independent eigenvectors.
-
Term: Jordan Form
Definition:
A canonical form of a matrix that generalizes diagonalization, representing a matrix as a block diagonal matrix, which includes Jordan blocks.