Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Algebraic and Geometric Multiplicity
Unlock Audio Lesson
Today, we are going to explore two important concepts: algebraic multiplicity and geometric multiplicity. Can anyone tell me what they think algebraic multiplicity represents?
I think it’s related to how many times an eigenvalue appears in the characteristic polynomial, right?
Correct! Algebraic multiplicity counts how many times an eigenvalue is repeated as a root of the polynomial. Now, what about geometric multiplicity?
Is it the number of linearly independent eigenvectors for that eigenvalue?
Exactly! Geometric multiplicity tells us how many different directions the eigenvalue can stretch or compress. Remember, GM must equal AM for diagonalizability, which is crucial in our applications.
Can you explain why that equality is so important?
Certainly! If GM is less than AM, it means we don't have enough independent directions to fully diagonalize the matrix. This concept will be important when we tackle examples and applications.
To summarize, AM counts roots, while GM counts independent vectors. Remember this distinction.
Examining a Non-Diagonalizable Matrix
Unlock Audio Lesson
Let’s look at our example matrix: A = [2, 1; 0, 2]. What can we identify about its eigenvalues?
It looks like the eigenvalue is λ = 2, and it appears twice, so the AM is 2.
Exactly! Now, how about the geometric multiplicity? What do we get when we solve (A - 2I)v = 0?
When we set up the matrix, it simplifies, but I think we end up with only one independent equation, giving GM = 1.
Right! So we’ve established AM of 2 and GM of 1. Since GM does not equal AM, what does that mean for matrix A?
It means A is not diagonalizable.
Great conclusion! This tells us that while the eigenvalue has a multiplicity, we don't have enough eigenvectors to structure a full diagonalization. It’s a key concept for various applications, such as in structural engineering.
Applications and Implications of Multiplicity
Unlock Audio Lesson
Now that we’ve seen the theoretical side, how do these concepts translate into real-world applications, particularly in civil engineering?
I guess in structural analysis, if a stiffness matrix is not diagonalizable, it could affect how we understand a structure’s response.
Exactly! If the matrix representing a system cannot be diagonalized due to AM not equaling GM, it impacts stability analysis and dynamic behavior predictions.
So, to achieve a stable design, we need to ensure we have enough independent eigenvectors?
Precisely, which is why diagonalizability is such an essential property! Let’s summarize by reiterating that understanding these multiplicities can critical impacts on engineering feasibility.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explores the definitions of algebraic multiplicity (AM) and geometric multiplicity (GM) of eigenvalues. It states that a matrix is diagonalizable if the geometric multiplicity equals the algebraic multiplicity for all its eigenvalues. A specific example illustrates a non-diagonalizable matrix to solidify understanding.
Detailed
Repeated Eigenvalues and Geometric Multiplicity
In linear algebra, the concepts of algebraic multiplicity (AM) and geometric multiplicity (GM) are crucial for understanding eigenvalues associated with matrices.
- Algebraic Multiplicity (AM) refers to the number of times an eigenvalue appears as a solution to the characteristic polynomial of a matrix.
- Geometric Multiplicity (GM) is defined as the number of linearly independent eigenvectors associated with a particular eigenvalue.
The key rule connecting these two concepts is that a matrix is diagonalizable if and only if the geometric multiplicity equals the algebraic multiplicity for each eigenvalue.
The section provides an example of a matrix that has repeated eigenvalues but is not diagonalizable. For instance, the matrix
a = [2 1]
[0 2]
has an eigenvalue λ = 2 with an algebraic multiplicity of 2 but only one linearly independent eigenvector, leading to a geometric multiplicity of 1. This discrepancy confirms that the matrix is not diagonalizable.
Understanding AM and GM is crucial for applications such as solving differential equations and stability analysis in engineering contexts.
Youtube Videos
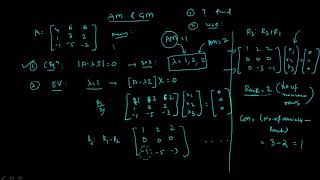
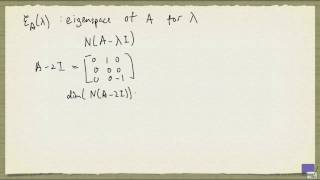
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Multiplicity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let’s dig deeper into multiplicity:
- Algebraic multiplicity (AM): Number of times an eigenvalue appears in the characteristic equation.
- Geometric multiplicity (GM): Number of linearly independent eigenvectors associated with that eigenvalue.
Detailed Explanation
This chunk introduces two key concepts related to eigenvalues: algebraic multiplicity and geometric multiplicity. The algebraic multiplicity (AM) of an eigenvalue is how many times that eigenvalue shows up as a solution in the characteristic equation of a matrix. For example, if a matrix has an eigenvalue of 2 that appears three times in its characteristic polynomial, then its AM is 3.
In contrast, the geometric multiplicity (GM) refers to the number of linearly independent eigenvectors corresponding to the same eigenvalue. To have full usefulness in many applications, the GM must equal the AM for a matrix to be diagonalizable. This means we need to have as many independent directions (eigenvectors) as there are repetitions of an eigenvalue.
Examples & Analogies
Think of algebraic multiplicity as the number of times a song is played on the radio (it could be quite often), while geometric multiplicity is like the number of distinct radio stations that play that song. If a song is played on multiple stations and you count each occurrence (AM), but you want to find out how many stations are actually playing it independently (GM). You need a station for each play to ensure you can hear it from different angles or interpretations.
Diagonalizability Condition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Key Rule: A matrix A is diagonalizable if GM = AM for all eigenvalues.
Detailed Explanation
This key rule states that a matrix is diagonalizable only when the geometric multiplicity (GM) is equal to the algebraic multiplicity (AM) for each of its eigenvalues. This equality ensures that there are enough independent eigenvectors to form a complete basis for the vector space in which the matrix operates. Therefore, if you find an eigenvalue whose GM is less than its AM, you can immediately conclude that the matrix cannot be diagonalized.
Examples & Analogies
Imagine trying to organize a group discussion. For every participant (an eigenvalue), you want to ensure that there are enough unique perspectives (independent eigenvectors). If one participant's views are repeated multiple times (high AM) but they can only bring one unique idea (low GM), then your discussion won't be as enriching, and you won't achieve a varied and comprehensive conversation (diagonalization).
Example of Non-Diagonalizable Matrix
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example of Non-Diagonalizable Matrix
A=
[2 1]
[0 2]
- Characteristic polynomial: ¿
- Eigenvalue: λ=2, AM = 2
A−2I=
[0 1]
[0 0]
Solving (A−2I)v=0 gives only one linearly independent eigenvector ⇒ GM = 1.
So, A is not diagonalizable.
Detailed Explanation
In this example, we're analyzing a specific matrix to determine its diagonalizability. The matrix has an eigenvalue, λ = 2, which appears twice in its characteristic polynomial (hence AM = 2). However, when we compute (A−2I) and solve for eigenvectors, we find that we can only extract one linearly independent eigenvector (GM = 1). This discrepancy between GM and AM indicates that we do not have sufficient independent eigenvectors to diagonalize the matrix, confirming that this matrix is not diagonalizable.
Examples & Analogies
Consider a project team where only one person knows how to handle a specific task, even though there are multiple people assigned to that role. If those extra people can only echo what the original team member says (one independent voice), then while you have many 'helpers' (high AM), you lack enough unique insights or solutions (low GM) to lead effectively. As a result, your team struggles to adapt or delegate more effectively, just like the matrix that can't be diagonalized.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Algebraic Multiplicity: Refers to how often an eigenvalue appears as a solution to the characteristic polynomial of a matrix.
-
Geometric Multiplicity: Represents the number of linearly independent eigenvectors associated with an eigenvalue.
-
Diagonalizability: A matrix is diagonalizable if the geometric multiplicity equals the algebraic multiplicity.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The matrix A = [2, 1; 0, 2] has an algebraic multiplicity of 2 and geometric multiplicity of 1, making it non-diagonalizable.
-
If a matrix has distinct eigenvalues, such as A = [1, 0; 0, 2], it is diagonalizable because GM = AM for each eigenvalue.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Algebraic counts the roots so true, geometric shows the directions too!
📖 Fascinating Stories
-
Imagine a book on a shelf (algebraic) with many copies of one title, but only a few readers (geometric)! The readers represent independent eigenvectors that define the new perspectives.
🧠 Other Memory Gems
-
Remember AM = ACount, GM = GeoMore. Where ACount tells you how many times it shows up, and GeoMore tells you how many are unique!
🎯 Super Acronyms
Remember 'AM = Roots' and 'GM = Vectors' to differentiate between algebraic and geometric multiplicity.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Algebraic Multiplicity (AM)
Definition:
The number of times an eigenvalue appears in the characteristic equation of a matrix.
-
Term: Geometric Multiplicity (GM)
Definition:
The number of linearly independent eigenvectors associated with a particular eigenvalue.
-
Term: Diagonalizable Matrix
Definition:
A matrix that can be expressed in the form A = PDP⁻¹, where P is an invertible matrix and D is a diagonal matrix.
-
Term: Eigenvalue
Definition:
A scalar that satisfies the equation Av = λv, where A is a matrix and v is a non-zero vector.