Diagonalization of Symmetric Matrices
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Properties of Symmetric Matrices
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today we're discussing symmetric matrices. Can anyone tell me what it means for a matrix to be symmetric?

I think it means that the matrix is equal to its transpose.

Exactly! A matrix **A** is symmetric if **A^T = A**. What do you think are some implications of this property?

Do symmetric matrices have special kinds of eigenvalues?

Great question! All eigenvalues of a real symmetric matrix are real numbers. Let's remember this key point: **Real Eigenvalues, Real Properties!**

Is it true that the eigenvectors are related to the eigenvalues in a special way?

Yes! Eigenvectors corresponding to distinct eigenvalues are orthogonal. This is a powerful concept in many applications, such as structural analysis.

So, if we have two eigenvalues, their corresponding eigenvectors will be at right angles to each other?

Exactly! Remember, orthogonality is key in simplifying many calculations. Let’s summarize what we discussed: symmetric matrices have real eigenvalues and orthogonal eigenvectors, which help in calculations.
Orthogonal Diagonalization
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we know the properties, let's discuss how we can diagonalize a symmetric matrix. Can someone explain what diagonalization involves?

Is it when we express a matrix in a diagonal form using its eigenvalues?

Exactly! We can express a symmetric matrix as **A = QDQ^T**, where **Q** is an orthogonal matrix and **D** is diagonal. Why do we think orthogonal diagonalization is particularly useful in engineering?

It makes calculations more stable, right? Like in structural engineering applications?

Correct! In structural engineering, ensuring numerical stability is crucial for processes like modal analysis. This leads us to an essential takeaway - **Orthogonal diagonalization ensures stability!**
Applications in Engineering
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s connect our knowledge with real-world applications. Can anyone think of an area in engineering where symmetric matrices are frequently found?

Maybe in analyzing vibrations of structures?

Yes! Stiffness matrices in structural analysis are symmetric. Why is this beneficial?

Because it allows us to use the diagonalization to simplify the equations we solve!

Exactly! Symmetric matrices provide natural frequency and mode shapes, critical in earthquake engineering. Let’s remember this: **Symmetry leads to stability in structural analysis!**
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we learn about symmetric matrices and their diagonalization. Key features include the fact that they have real eigenvalues and orthogonal eigenvectors, ensuring stable numerical applications in engineering. The section also highlights the role of orthogonally diagonalizable matrices in simplifying complex calculations in engineering contexts.
Detailed
Diagonalization of Symmetric Matrices
Diagonalization is a fundamental concept in linear algebra where a square matrix can be simplified into a diagonal matrix for easier computations. A matrix A is symmetric if it equals its transpose (i.e., A^T = A). This section outlines the special properties that real symmetric matrices exhibit:
- Real Eigenvalues: All eigenvalues of a symmetric matrix are real numbers, unlike general matrices which may have complex eigenvalues.
- Orthogonal Eigenvectors: Eigenvectors corresponding to distinct eigenvalues of a symmetric matrix are orthogonal (perpendicular to each other). This is pivotal in applications requiring independent modes, such as vibration analysis in civil engineering.
- Orthogonal Diagonalization: Any real symmetric matrix can be orthogonally diagonalized, represented as A = QDQ^T, where Q is an orthogonal matrix (meaning Q^T = Q^(-1)) and D is a diagonal matrix composed of the eigenvalues of A.
The utility of these properties is significant in structural engineering applications, such as ensuring numerical stability during calculations involving stiffness matrices, which are typically symmetric due to material properties and structural configurations. Overall, this section emphasizes the mathematical underpinnings of diagonalization in symmetric matrices and its implications in engineering practices.
Youtube Videos
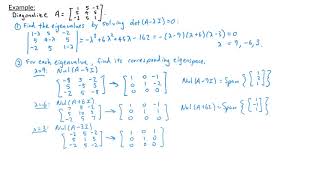



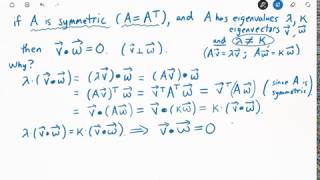





Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Symmetric Matrices
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
A matrix A is symmetric if AT = A.
Detailed Explanation
A symmetric matrix is one that is equal to its transpose. This means that for any element a_ij in the matrix, it holds that a_ij = a_ji. In simpler terms, if you flip the matrix over its diagonal, the matrix remains unchanged.
Examples & Analogies
Think of a symmetric matrix like a perfectly balanced seesaw. No matter how you look at it, the side with the weight will always look directly opposite to the other side. This balance and equality are what characterize a symmetric matrix.
Properties of Eigenvalues in Symmetric Matrices
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In the case of real symmetric matrices, the diagonalization process has some special properties:
- All eigenvalues of a symmetric matrix are real.
- Eigenvectors corresponding to distinct eigenvalues are orthogonal.
Detailed Explanation
One of the crucial properties of real symmetric matrices is that their eigenvalues (the scalars that measure the factor by which the eigenvectors are scaled during the transformation) are always real numbers, not complex. Furthermore, if two eigenvalues are different, the corresponding eigenvectors will be at right angles (orthogonal) to each other. This is important in applications where independent directions of movement or forces are considered.
Examples & Analogies
Imagine a 3D room. If you have two directions in the room, like going straight ahead and turning to the left, those two directions are independent of each other. In a symmetric matrix, the eigenvectors show us these independent directions, and they won't interfere with each other, specific to respective eigenvalues.
Orthogonal Diagonalization
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
A real symmetric matrix is always orthogonally diagonalizable: That is, A=QDQT where:
- Q is an orthogonal matrix (QT = Q−1),
- D is a diagonal matrix with real eigenvalues.
Detailed Explanation
Orthogonal diagonalization means that we can express a symmetric matrix A as the product of an orthogonal matrix Q and a diagonal matrix D. The orthogonal matrix Q contains eigenvectors as its columns, and these eigenvectors are orthonormal (they have unit length and are mutually perpendicular). Because Q is orthogonal, multiplying by its transpose simplifies computations when dealing with inverse operations.
Examples & Analogies
Consider a DVD player that plays movies: you can think of the orthogonal matrix Q as the player, simplifying the 'movie' (the matrix A) into clearer aspects (the diagonal matrix D) without losing any information, just like a high-quality resolution enhances movie playback.
Importance in Structural Engineering
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In structural engineering, stiffness matrices are symmetric due to physical principles. Orthogonal diagonalization ensures numerical stability and simplified modal analysis.
Detailed Explanation
In applications such as structural engineering, it is essential that the mathematical models used (like stiffness matrices) exhibit properties of symmetry. This allows engineers to make accurate predictions about how structures behave under loads. Orthogonal diagonalization aids in simplifying analyses (like modal analysis) and ensures that numerical methods yield stable results.
Examples & Analogies
Think of a bridge as it sways with the wind. The stiffness matrix represents the bridge's capability to withstand these forces. Using symmetric properties ensures engineers can accurately predict its performance, much like using the right materials to ensure the bridge won't sway too much under pressure.
Key Concepts
-
Diagonalization: The process of converting a matrix into diagonal form.
-
Symmetric Matrix: A matrix that is equal to its transpose.
-
Real Eigenvalues: Symmetric matrices have eigenvalues that are real numbers.
-
Orthogonal Eigenvectors: Eigenvectors corresponding to distinct eigenvalues are orthogonal.
-
Orthogonal Diagonalization: Expressing a matrix as A = QDQ^T where Q is orthogonal and D is diagonal.
Examples & Applications
For a symmetric matrix like [4 -2; -2 4], the eigenvalues calculated would be real, and its eigenvectors are orthogonal.
In structural engineering, the stiffness matrix of a system is often symmetric, ensuring stability in dynamic analysis.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
A symmetric matrix is quite legit, transpose it, it must fit!
Stories
Imagine two knights, standing on a symmetrical chessboard. If one knight moves, the other must mirror it; this reflects how eigenvectors of symmetric matrices behave - they mirror and remain consistent.
Memory Tools
Remember 'RED' - Real eigenvalues, Distinct orthogonal vectors when thinking about symmetric matrices.
Acronyms
S.O.S - Symmetric, Orthogonal, Stable.
Flash Cards
Glossary
- Symmetric Matrix
A square matrix that is equal to its transpose (A^T = A).
- Eigenvalue
A scalar value associated with a linear transformation, indicating the factor by which the eigenvector is scaled.
- Eigenvector
A non-zero vector that changes at most by a scalar factor when a linear transformation is applied.
- Orthogonal Matrix
A square matrix whose rows and columns are orthogonal unit vectors, satisfying the condition Q^T = Q^(-1).
- Diagonal Matrix
A matrix in which the entries outside the main diagonal are all zero.
Reference links
Supplementary resources to enhance your learning experience.
