Auxiliary Equation and General Solution
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Auxiliary Equation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we’re diving into the auxiliary equation for second-order linear homogeneous differential equations. Can anyone tell me what form our general equation takes?

Isn't it something like d²y/dx² + p dy/dx + qy = 0?

Exactly! Now, when we assume a solution of the form y = e^{mx}, what do we do next?

We substitute that into the equation!

Correct! This gives us the auxiliary equation: m² + pm + q = 0. Why do you think this is important?

Because it helps us find the roots that tell us the form of our solution!

Fantastic summary! Understanding the roots helps us predict the behavior of our differential equation solutions.
Types of Roots and Their Solutions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we've established the auxiliary equation, let’s discuss how the nature of the roots affects our solutions. What happens when we have real and distinct roots?

We have two different exponential solutions, right?

Yes! The general solution is y(x) = C₁ e^{m₁x} + C₂ e^{m₂x}. What if the roots are real and repeated?

Then we need to add a linear term with x, so it's y(x) = (C₁ + C₂ x)e^{mx}!

Great job! One last case: what about complex roots?

We get a solution involving sine and cosine, y(x) = e^{αx}(C₁ cos(βx) + C₂ sin(βx)).

Exactly! These forms are so helpful in application, especially in engineering scenarios like vibrations.
Examples of Different Solutions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s look at some practical examples of our different solutions. Who wants to start with real and distinct roots?

I can! For example, the equation d²y/dx² - 5dy/dx + 6y = 0 has the auxiliary equation m² - 5m + 6 = 0.

Right! And what roots do we get?

They’re m = 2 and m = 3!

Good! So the general solution is y(x) = C₁ e^{2x} + C₂ e^{3x}. Now, what about repeated roots?

For d²y/dx² - 4dy/dx + 4y = 0, we find m = 2 is repeated, giving us y(x) = (C₁ + C₂ x)e^{2x}.

Perfect! Lastly, let’s discuss complex roots.

For d²y/dx² + 4y = 0, we get roots m = ±2i, leading to the solution y(x) = C₁ cos(2x) + C₂ sin(2x).

Excellent examples! Remember that these techniques apply to many engineering problems, especially in vibrations.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we explore the concept of the auxiliary equation for second-order linear homogeneous differential equations, detailing the methods for finding general solutions based on real and distinct roots, repeated roots, and complex roots. This foundational knowledge is crucial for engineering applications and modeling real-world phenomena.
Detailed
Auxiliary Equation and General Solution
This section focuses on the auxiliary equation associated with second-order linear homogeneous differential equations of the form:
$$\frac{d^2y}{dx^2} + p \frac{dy}{dx} + qy = 0$$
We begin by assuming a solution of the form \(y = e^{mx}\) and substitute this into the differential equation. This leads to the auxiliary equation (also known as the characteristic equation):
$$m^2 + pm + q = 0$$
The roots of this polynomial play a crucial role in determining the general solution of the differential equation:
- Real and Distinct Roots: If the roots \(m_1\) and \(m_2\) are distinct real numbers, the general solution is:
$$y(x) = C_1 e^{m_1 x} + C_2 e^{m_2 x}$$
- Real and Repeated Roots: If the roots are the same (i.e., \(m_1 = m_2 = m\)), the general solution takes the form:
$$y(x) = (C_1 + C_2 x)e^{mx}$$
- Complex Roots: If the roots are complex conjugates (expressed as \(m = \alpha \pm i \beta\)), the solution becomes:
$$y(x) = e^{\alpha x}(C_1 \cos(\beta x) + C_2 \sin(\beta x))$$
Understanding these forms helps in modeling various engineering phenomena, from structural responses to thermal distributions.
Youtube Videos





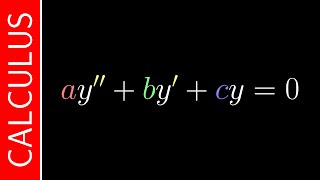




Audio Book
Dive deep into the subject with an immersive audiobook experience.
Formulating the Differential Equation
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
To solve:
d2y d y
+p +qy=0
dx2 dx
Detailed Explanation
We begin with the standard form of a second-order linear homogeneous differential equation, which includes second derivatives and coefficients that depend on the independent variable. Here, 'p' and 'q' represent coefficients that are used throughout the solution process. This sets up the need to find a function 'y' that satisfies this equation for all values of 'x'.
Examples & Analogies
Think of this as trying to balance forces in engineering: just as different forces act on a structure, different terms in the equation act on the solution we seek.
Assuming a Solution
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
We assume a solution of the form:
y=emx
Detailed Explanation
To solve the differential equation, we assume a solution that takes an exponential form, specifically 'y = e^(mx)', where 'm' is a constant. This type of function is often used in differential equations because it simplifies the process of finding the roots of the equation you will encounter later.
Examples & Analogies
Imagine the population growth of bacteria in a lab environment; if conditions are ideal, the number of bacteria can grow exponentially, similar to how 'e^(mx)' behaves.
Substitution into the Differential Equation
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Substituting into the differential equation:
m2emx +pmemx +qemx =0
emx (m2 +pm+q)=0
Detailed Explanation
By substituting the assumed solution back into the original differential equation, we can factor out the exponential function, which simplifies our work significantly. This leads us to focus on the polynomial term '(m^2 + pm + q)', which is crucial in determining the nature of the solutions.
Examples & Analogies
This step is akin to solving for the roots of a quadratic equation in mathematics. Just as knowing the roots gives insight into a parabola's vertex, here identifying 'm' will help determine the behavior of our solution.
Defining the Auxiliary Equation
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Since emx≠0,
the auxiliary equation (characteristic equation) is:
m2 +pm+q=0
Detailed Explanation
Since the exponential term 'e^(mx)' is never zero, we can set the equation inside the parentheses to zero. This gives us the auxiliary equation, or characteristic equation, which is a crucial step to determine the nature of 'm' that will help us form the general solution of the differential equation.
Examples & Analogies
Imagine finding a specific combination of ingredients for a recipe. The auxiliary equation helps us pinpoint the specific values we need to achieve the desired 'flavor' or result in the solution.
Nature of the Roots and General Solution
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The nature of the roots of the auxiliary equation determines the form of the general solution.
Detailed Explanation
The roots of the auxiliary equation can be real and distinct, real and repeated, or complex conjugates. Each case leads to a different form of the general solution, significantly affecting how the overall solution behaves over time. Understanding these distinctions is crucial for applying the general solution appropriately in practical problems.
Examples & Analogies
Consider a car's acceleration: if the engine works efficiently (real and distinct roots), the car speeds up rapidly; if there's some resistance (repeated roots), the car might accelerate but at a slower rate; and if there are issues with the engine (complex roots), the car may behave erratically, reflecting the types of solutions we investigate.
Key Concepts
-
Auxiliary Equation: Determines the nature of solutions based on the roots.
-
General Solution: Formulated from the roots of the auxiliary equation.
-
Real and Distinct Roots: Lead to exponential solutions.
-
Repeated Roots: Introduce linear terms in the solution.
-
Complex Roots: Result in oscillatory solutions involving trigonometric functions.
Examples & Applications
Example 1: Solve d²y/dx² - 5dy/dx + 6y = 0. Roots: m = 2, m = 3. General solution: y(x) = C₁ e^{2x} + C₂ e^{3x}.
Example 2: Solve d²y/dx² - 4dy/dx + 4y = 0. Roots: m = 2 (repeated). General solution: y(x) = (C₁ + C₂ x)e^{2x}.
Example 3: Solve d²y/dx² + 4y = 0. Roots: m = ±2i. General solution: y(x) = C₁ cos(2x) + C₂ sin(2x).
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
For roots that are rooted, to solutions we'd go, Real, complex, and repeated, the answers will flow!
Stories
Once upon a time, in the valley of equations, three brothers — Real, Complex, and Repeated — set off on a quest to find their solutions in the wild land of Mathematics.
Memory Tools
R.C.R. stands for Real, Complex, Repeated — remember to categorize your roots!
Acronyms
Through 'A.R.C.', think of Auxiliary for Roots and Cases
Differential solutions based on character!
Flash Cards
Glossary
- Auxiliary Equation
The characteristic equation derived from a second-order linear homogeneous differential equation, determining the nature of the roots.
- General Solution
The complete solution to a differential equation including arbitrary constants determined by initial or boundary conditions.
- Real Roots
Roots of the auxiliary equation that are distinct and not complex.
- Complex Roots
Roots of the auxiliary equation that include imaginary numbers, resulting in sine and cosine components in the general solution.
- Repeated Roots
Two identical roots of the auxiliary equation, leading to a modified general solution that includes a linear term.
Reference links
Supplementary resources to enhance your learning experience.
