Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Concept of Repeated Roots
Unlock Audio Lesson
Good morning, class! Today, we're diving into a special case of differential equations known as real and repeated roots. Can anyone tell me what we mean by a repeated root?
Is it when roots of the auxiliary equation are the same?
Exactly! When both roots m₁ and m₂ from the auxiliary equation are equal, that’s what we call a repeated root. Now, what happens to our general solution in that case?
It changes, right? It becomes different from the case with distinct roots.
Correct! The general solution takes the form $$y(x) = (C_1 + C_2 x)e^{mx}$$. The linear term C₂x appears due to that repeat. Can anyone think of why this might happen?
It could represent how the system behaves when there's not enough damping?
Good thought! In a way, it helps us model unique behaviors in systems encountering limits or critical conditions. Let’s summarize: repeated roots indicate how solutions adjust and diversify due to the multiplicity of conditions.
Finding the Equations and Solutions
Unlock Audio Lesson
Let’s consider we have an auxiliary equation that outputs repeated roots. For instance, consider one such equation: $$m^2 - 4m + 4 = 0$$. How would we go about solving this, and what would we find?
We factor that into (m-2)² = 0, meaning m=2 is a repeated root.
Excellent! Thus, substituting back into our solution format, what will our general solution look like?
It would be $$y(x) = (C_1 + C_2 x)e^{2x}$$.
Right again! This form indicates how we expect the system to respond to initial conditions when there’s lack of variability due to damping. Remember, this also showcases the engineering principle of redundancy!
Applications of Repeated Roots in Engineering
Unlock Audio Lesson
How do repeated roots from our solutions affect real-world engineering applications? Can any of you think of a civil engineering context?
Maybe something related to the stability of structures, like columns?
That’s a great application! In column buckling problems, repeated roots can illustrate critical load conditions leading to potential instability. How would we use this in practice?
We would determine the load at which the column reaches that point of instability using our derived solutions?
Exactly! Engineers depend on these methodologies for designing safer structures. If we understand the dynamics of repeated roots, we can anticipate structural behaviors. Let’s summarize the importance of repeated roots in practical applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the nature of real and repeated roots for second-order linear homogeneous differential equations, highlighting how these roots affect the general solution form. The significance of the multiplicity of roots is emphasized, using concrete examples to illustrate the concept.
Detailed
Case II: Real and Repeated Roots
In studying second-order linear homogeneous differential equations, we encounter various types of roots found in the auxiliary (characteristic) equation. In Case II, we specifically examine real and repeated roots, denoting them as follows:
If the roots are equal, represented as m₁ = m₂ = m, the general solution takes the form:
$$y(x) = (C_1 + C_2 x)e^{mx}$$
In this format, the solution indicates that the standard exponential decay or growth is modified by an additional linear term (Cx), which arises due to the multiplicity of the root. This phenomenon is particularly relevant in scenarios like critical damping in oscillations, where unique solution behavior is observed. Thus, understanding this case allows engineers to predict and model dynamic behavior accurately in structures such as beams and columns.
Youtube Videos
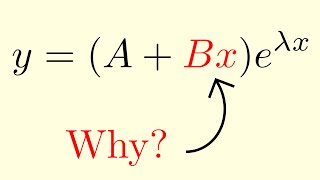
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Repeated Roots
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If the roots are real and equal, say m₁ = m₂ = m, then: y(x) = (C₁ + C₂x)e^{mx}
Detailed Explanation
In this scenario, we examine what happens when a differential equation has roots that are not just real, but also repeated. When we say that the roots are equal, it means that they represent the same value, which affects how we formulate our solution. In mathematical terms, if both roots (denoted m₁ and m₂) are equal to m, instead of having two independent solutions as we do with distinct roots, we combine their effects. This leads to a solution in which we include a linear term (C₂x) in addition to the standard exponential part. This change reflects the fact that the repeated root increases the multiplicity of the solution space, allowing us to form a more complex solution that still adheres to the structure necessary for the differential equation.
Examples & Analogies
Think of this like a music note being played at the same pitch repeatedly. If you play a note at a constant volume, it resonates in a particular way that can be distinct. But if you press on the key longer (like allowing a note to sustain), you're adding layers to that sound. In engineering structures, this might be seen in the behavior of a beam that experiences consistent loading at a specific point: the response is not just a simple bending but becomes more complex and nuanced, similar to how our musical note's sound develops with time.
General Solution with Repeated Roots
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This accounts for the multiplicity of the solution space.
Detailed Explanation
The phrase 'this accounts for the multiplicity of the solution space' highlights the importance of considering repeated roots when forming solutions to differential equations. In contrast to distinct roots, which provide separate and individual solutions, repeated roots lead to a singular, compounded effect that requires us to encode this complexity into our solution format. This means we need to account for both the principal response given by the repeated root and how small changes (represented by C₂x) affect the overall response. The fact that we can write our solution in this way mirrors many physical systems, where interactions tend to produce more complex outcomes than when simply summed individual effects.
Examples & Analogies
Imagine planting a tree with two branches that grow from a single trunk. The trunk is like the repeated root that establishes the foundational structure, while the branches represent those additional responses that grow out of it. Although the trunk is crucial for supporting the tree, it’s the interaction of both the trunk and branches—just like the C₁ and C₂ terms in our solution—that shapes the overall growth of the tree, illustrating how systems can evolve more intricately than expected.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Real and Repeated Roots: Characteristics of roots affecting the form of the general solution in differential equations.
-
Auxiliary Equation: The polynomial equation used to derive the characteristic roots from which solutions are obtained.
-
General Solution Form: Indicates the different expressions of solutions depending on the type of roots.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of repeated roots: m² - 4m + 4 = 0 leads to $$y(x) = (C_1 + C_2 x)e^{2x}$$.
-
Application in structural analysis: Critical loads in columns can be determined using the general solution for repeated roots.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
If roots repeat, a new form’s the treat, C and Cx, your solutions compete.
📖 Fascinating Stories
-
Imagine a bridge that starts to sway under weight; it dances on doubled roots that regulate its fate, providing stability while growing in weight.
🧠 Other Memory Gems
-
Remember: R for Repeated means Resilience in design, reflecting how structures intertwine!
🎯 Super Acronyms
R.E.A.P
- Repeated roots Enhance Adjustments for Predictability in structures.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Root
Definition:
A solution to the auxiliary or characteristic equation derived from a differential equation.
-
Term: Repeated Root
Definition:
A root that occurs more than once in the characteristic equation, leading to a specific form of the general solution.
-
Term: General Solution
Definition:
The complete form of the solution to a differential equation, encompassing all particular solutions through arbitrary constants.
-
Term: Auxiliary Equation
Definition:
The polynomial equation derived from substituting a trial solution into the differential equation, used to find the characteristic roots.