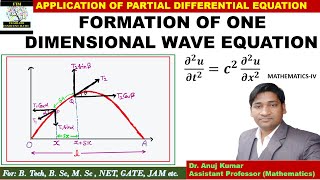
Derivation of the One-Dimensional Wave Equation
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Transverse Displacement
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will learn about transverse displacement in wave motion. When we look at a vibrating string, can anyone tell me what transverse displacement means?

I think it refers to how the string moves up and down.

Exactly! Transverse displacement, u(x, t), describes how far a point on the string moves vertically from its rest position at point x and time t. Why is it important for wave equations?

Because it helps us understand how waves propagate along the string!

Correct! Remember, this displacement is what we analyze to derive our wave equation.
Forces Acting on the String
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s discuss the forces acting on our small element of the string. What do you think happens at the ends of the small segment between x and x+Δx?

The tension will create forces that cause it to move!

Right! The tension at position x generates a force that’s dependent on the angle of the string. We represent the vertical force difference using trigonometric approximations. Can anyone remember what they are?

I think it's T sin(θ + Δθ) - T sin(θ).

Exactly! We can simplify this using small-angle approximations to find the net force acting on the element. This leads us toward deriving the wave equation.
Deriving the Wave Equation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s progress to deriving the wave equation. From our force balance, we established the net vertical force and related it to the mass and acceleration of the string segment. Can anyone state the equation we obtain?

It results in TΔx = ρΔx ∂²u/∂t²!

Exactly! By cancelling out the Δx, we derive our one-dimensional wave equation: \( \frac{\partial^{2}u}{\partial t^{2}} = c^{2} \frac{\partial^{2}u}{\partial x^{2}} \). What does c represent?

It's the wave speed, which relates tension and density!

Correct! Great job everyone—we've just derived the wave equation that will help us analyze wave motions in various applications.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section explains how the wave equation for a vibrating string is obtained by analyzing a small segment of the string under the influence of tension and applying Newton's second law to derive the equation that governs wave motion. It emphasizes the significance of constant tension and uniform linear density in formulating the wave equation.
Detailed
Detailed Summary
The one-dimensional wave equation is derived in this section by examining a vibrating string of length L that is taut between two fixed supports. A small segment of the string, identified as an element between position x and x+∆x, is analyzed. The tension in the string creates a transverse force, which can be expressed as the difference in the vertical components of the tension force at either end of the segment.
By applying Newton's second law to this segment, we derive an equation of motion for the transverse displacement, u(x, t), leading us to the core wave equation:
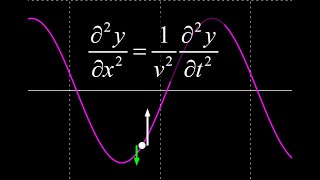
\[ \frac{\partial^{2}u}{\partial t^{2}} = c^{2} \frac{\partial^{2}u}{\partial x^{2}} \]
where c is the wave speed, defined as \( c = \sqrt{\frac{T}{\rho}} \), with T being the tension and ρ the uniform linear density of the string. This derivation lays the foundation for further analysis of wave motion, including boundary conditions, initial conditions, and solution techniques in wave mechanics, which is essential in applications ranging from structural engineering to musical acoustics.
Youtube Videos







Audio Book
Dive deep into the subject with an immersive audiobook experience.
Defining the Problem
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let the string extend from x=0 to x=L, and let u(x,t) denote the transverse displacement at position x and time t.
Detailed Explanation
In this initial step, we establish the context of the problem by defining the string's length and how we measure displacement. Here, u(x,t) signifies the displacement of the string from its rest position at a point x along the length of the string and at a time t. Essentially, we are setting up a system to understand how the string moves back and forth due to vibrations.
Examples & Analogies
Think of a guitar string; when you pluck it, you can see the string moving up and down. The displacement u(x,t) represents how far the string is at any point from its original position at any moment.
Analyzing Forces on a Small Element
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Consider a small element of the string between x and x+∆x. Let the tension at position x be T, and the angles made by the string with the horizontal at x and x+∆x be θ and θ+∆θ, respectively.
Detailed Explanation
Here, we are examining a small segment of the string. We denote this small piece of string as being between two points, x and x + ∆x. The tension (T) represents the force that is pulling on the string, while θ and ∆θ describe the angles of this segment relative to the horizontal. This particular setup helps us understand how forces act on different parts of the string and are vital for calculating the resulting motion.
Examples & Analogies
Imagine you are holding a slinky stretched between two points. The tension in the slinky pulls it straight, but if you wiggle one end, the forces cause the coils to shift at different angles. This is similar to what we are observing in this portion of the string.
Transverse Force Balance
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Using Newton’s second law in the vertical direction:
Net vertical force=ρ∆x
∂2u
∂t2
(cid:18) (cid:19)
T sin(θ+∆θ)−T sin(θ)≈T (x+∆x)− (x)
∂u ∂u
t=
T ∆x
t={}
∂x ∂x
∂2u
=T ∆x
∂x2
Detailed Explanation
In this chunk, we apply Newton's second law, which states that the net force acting on an object is equal to its mass times acceleration. We focus only on the vertical forces acting on our small piece of the string. The net vertical force acting on this segment relates to the tension difference between the adjacent segments, which can be approximated using small-angle approximations. Ultimately, this leads us to relate the forces to the acceleration of the string segment, helping us to derive the wave equation.
Examples & Analogies
Imagine pulling a rope up with a steady force while someone else pulls it down with a much smaller force. The difference in the forces will cause a change in the acceleration of the rope. This situation parallels how we balance forces in our string segment.
Deriving the Wave Equation
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Equating force and acceleration:
∂2u ∂2u
T ∆x=ρ∆x
∂x2 ∂t2
Cancelling ∆x, we obtain the one-dimensional wave equation:
∂2u ∂2u
=c2
∂t2 ∂x2
where c=p T/ρ is the wave speed.
Detailed Explanation
After establishing the relationship between acceleration and the force due to tension, we equate these two concepts to derive our core equation. We simplify the equation by canceling out the small segment length (∆x), leading us to the famous wave equation in one dimension: the acceleration of the displacement over time and space relates by the constant c, which signifies the wave speed. This relationship allows us to model wave motion mathematically.
Examples & Analogies
This derivation is similar to how we calculate the speed of a wave in water. If you throw a stone in a pond, the ripples that spread are dictated by the tension of the water (how tightly it is held together) and the density of the water, which determines how quickly the waves travel.
Key Concepts
-
Transverse Displacement: Refers to the vertical movement of a segment of the string.
-
Wave Equation: Governs the dynamics of wave propagation, relating acceleration to displacement.
-
Constant Tension: The assumption that the tension remains unchanged during vibrations is crucial for deriving the wave equation.
Examples & Applications
Analyzing the motion of a guitar string when plucked to illustrate wave propagation.
Studying the behavior of a suspension bridge cable under varying tension to observe transverse displacements.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Tension and tone, as the string gets grown; waves up and down, in rhythm are shown.
Stories
Imagine a tightrope walker on a string. When the wind blows, they sway, and we can measure how far they move up and down. This is just like the transverse displacement in our wave equation!
Memory Tools
TDS: Tension, Displacement, Speed – key factors in wave dynamics.
Acronyms
TUD
Tension
Uniformity
Dynamics – essentials for understanding the wave equation.
Flash Cards
Glossary
- Transverse Displacement (u(x,t))
The vertical movement of a point on the vibrating string from its equilibrium position at a given time and position along the string.
- Wave Equation
A second-order partial differential equation that describes the propagation of waves, represented as \( \frac{\partial^{2}u}{\partial t^{2}} = c^{2} \frac{\partial^{2}u}{\partial x^{2}} \).
- Wave Speed (c)
The speed at which waves propagate through the medium, given by the formula \( c = \sqrt{\frac{T}{\rho}} \).
Reference links
Supplementary resources to enhance your learning experience.
