Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Eigenvalues
Unlock Audio Lesson
Today we'll start by discussing eigenvalues. Can anyone tell me what an eigenvalue is in the context of vibration?
Is it related to the solutions of differential equations?
Exactly! Eigenvalues arise from the solutions to the wave equation, particularly in systems with fixed boundaries. They help us characterize the vibrational modes.
What are these eigenvalues used for in engineering?
Great question! They determine the natural frequencies of vibration, which is crucial for ensuring the structure does not resonate under operational loads.
So if we avoid specific frequencies, we can prevent structural failure?
Exactly right! This is why analyzing eigenvalues is of critical importance in structural engineering.
So to remember: Eigenvalues help us find safe operational limits. Think of them as the 'safety frequencies' to avoid!
Natural Modes of Vibration
Unlock Audio Lesson
Now, let's discuss how each eigenvalue corresponds to a specific mode shape. Can anyone give me an example of a mode shape?
Isn't the sine function used in mode shapes?
Correct! The mode shapes can be represented as X(x) = sin(nπx/L), with n being the mode number. Each n gives us a different mode shape!
What happens to these modes at different frequencies?
Good question! As the frequency increases, you'll see more oscillations or 'nodes' in the mode shape. These nodes are points that remain stationary.
Remember: Each mode shape helps predict how a system will respond during vibrations!
Avoiding Resonance
Unlock Audio Lesson
Now let's talk about the practical application of what we've discussed. How do we use eigenvalues in design?
We need to ensure that our operational frequencies do not match the natural frequencies!
Exactly! This is known as avoiding resonance—a critical factor in structural safety.
What if a frequency matches, though? What happens?
If operational frequencies align with a natural frequency, resonance can occur, leading potentially to catastrophic failure due to excessive vibrations.
So, how do engineers prevent this?
Engineers often use damping strategies and design adjustments to shift natural frequencies away from anticipated operational frequencies. Always remember: Safety first, vibrations second!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore how each solution of the wave equation corresponds to a natural mode of vibration in structural systems, highlighting the significance of eigenvalues and their connection to resonance in engineering designs.
Detailed
In structural systems, each solution of the wave equation under fixed boundary conditions corresponds to natural modes or normal modes of vibration. These modes are critical for understanding the dynamic behavior of structures. Eigenvalues, represented as λ_n = (nπ/L)², are associated with each mode shape, which can be described by the function X(x) = sin(nπx/L). The corresponding natural frequencies ω_n = (nπc/L) determine the operational limits of a structure to avoid resonance, emphasizing the importance of this analysis in engineering design.
Youtube Videos
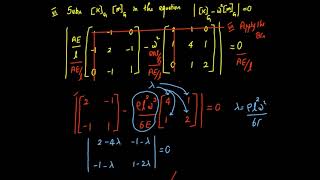
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Natural Modes of Vibration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In structural systems, each solution of the wave equation with fixed boundary conditions corresponds to a natural mode or normal mode of vibration. These modes have critical engineering significance:
Detailed Explanation
In structural engineering, systems like bridges or buildings vibrate when disturbed. The wave equation, which describes how vibrations travel through these structures, produces solutions that correspond to specific patterns of vibration known as 'modes.' Each mode represents a specific way in which a structure can vibrate when it is fixed at its boundaries (like the ends of a string). This is important for engineers because understanding these modes helps in anticipating how the structure behaves under various conditions, ensuring safety and durability.
Examples & Analogies
Think of a guitar string being plucked. The various sounds produced correspond to different frequencies or modes of vibration of the string. Each mode has a specific pattern of motion, and the resulting sound will depend on which modes are excited. Similarly, when buildings vibrate, they have modes that engineers must understand to prevent structural failures.
Eigenvalues and Mode Shapes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Recall from separation of variables: λ_n = (nπ/L)^2. Each λ corresponds to a mode shape: X(x) = sin(nπx/L) and associated natural frequency: ω_n = (nπc/L). These frequencies must be analyzed to avoid resonance in structural designs.
Detailed Explanation
The eigenvalues (λ_n) calculated from the wave equation play a crucial role in identifying the specific modes of vibration for a structural element. Each eigenvalue corresponds to a shape of vibration (mode shape) represented by a sine function. The natural frequencies (ω_n) give us the speed at which these modes vibrate. It is essential for engineers to analyze these frequencies because if external forces (like wind or earthquakes) match these frequencies, it can lead to resonance, which might cause the structure to fail.
Examples & Analogies
Imagine pushing someone on a swing at the right moment to make them go higher; that's resonance. In buildings, if gusts of wind match one of the building's natural frequencies, the vibrations might increase, leading to dangerous swaying. Engineers must ensure that structures can withstand or avoid these resonant frequencies to maintain safety.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Eigenvalues: Critical for determining natural frequencies.
-
Natural Modes: Defined by sine functions and shape characteristics.
-
Resonance: An important consideration in design to prevent structural failure.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a suspension bridge, the eigenvalues help determine the frequencies at which the bridge might resonate due to wind or traffic.
-
For a guitar string, the fundamental frequency and its harmonics can be identified using its eigenvalues.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Eigenvalues decide the tunes, when structures vibrate like bassooned balloons.
📖 Fascinating Stories
-
Imagine a bridge swaying as wind blows; the eigenvalues determine its dance and the frequencies it chose.
🧠 Other Memory Gems
-
E.N.F. - Eigenvalues, Natural frequency, and avoid Resonance!
🎯 Super Acronyms
E.N.F. = Eigenvalues (determine), Natural Frequency (resonate), Free to Fail (avoid).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Eigenvalue
Definition:
A scalar value associated with a linear transformation that indicates the factor by which a corresponding eigenvector is scaled.
-
Term: Natural Mode
Definition:
Distinct patterns of vibration that correspond to specific frequencies in a vibrating system.
-
Term: Resonance
Definition:
The condition when the frequency of an external force matches a system's natural frequency, leading to increased amplitude of oscillation.