Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Damping
Unlock Audio Lesson
Today, we're discussing damping in vibrating systems. Damping refers to the effect that reduces the amplitude of vibrations over time. Can anyone tell me why damping is important in engineering?
Because it helps control vibrations?
Exactly! Damping controls vibrations, improving the structure's safety and comfort. There are three types of damping we will cover: underdamped, critically damped, and overdamped systems.
What do those terms mean?
Good question! Let's dive deeper into each type of damping.
Underdamped Systems
Unlock Audio Lesson
An underdamped system oscillates with decreasing amplitude over time. Can anyone explain how this affects the vibrations?
They continue to move up and down, just more slowly?
Correct! This oscillation results in what we call a 'ringing' effect as the energy dissipates gradually.
So does that mean they take longer to settle down?
Yes! They do take longer to settle than critically damped systems. Let's move on to critically damped systems.
Critically Damped Systems
Unlock Audio Lesson
In critically damped systems, the return to equilibrium is achieved without oscillation, as quickly as possible. What benefits do you think critically damped systems provide in engineering structures?
They stabilize quickly?
Exactly! They are beneficial for minimizing structural oscillations after a disturbance. Now, what about overdamped systems?
Do they return to equilibrium very slowly?
Exactly right! Overdamped systems take the longest to settle compared to underdamped and critically damped systems.
Applications of Damping
Unlock Audio Lesson
Damping has crucial applications in civil engineering. Can anyone name a structure that uses damping devices?
Tall buildings or bridges?
That's correct! Damping devices in these structures help control vibrations, enhancing both safety and comfort for occupants.
How does that help in earthquakes?
Great follow-up! Damping helps to dissipate the energy from seismic waves, preventing structural damage.
Conclusion on Damping Effects
Unlock Audio Lesson
Today, we discussed the effects of damping. Who can summarize what we learned about underdamped, critically damped, and overdamped systems?
Underdamped oscillates slowly, critically damped returns quickly without oscillation, and overdamped returns slowly.
Excellent summary! Understanding these concepts enhances our ability to design safer engineering structures.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section delves into the effects of damping on the wave equation related to vibrating strings in engineering applications. It categorizes systems based on damping levels, such as underdamped, critically damped, and overdamped, and emphasizes the importance of understanding these concepts for enhancing structural safety and comfort.
Detailed
In structural engineering, damping significantly alters the vibrational behavior of systems. The wave equation for a vibrating string is modified to include a damping term, represented by the damping coefficient β. Different damping scenarios affect how the system oscillates:
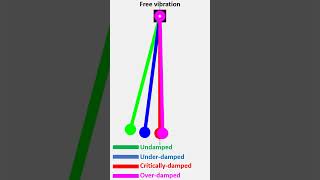
- Underdamped Systems: These oscillate with gradually decreasing amplitude, showcasing a characteristic 'ringing' effect.
- Critically Damped Systems: Return to equilibrium swiftly without oscillating, optimizing return speed.
- Overdamped Systems: These also return to rest without oscillation but more slowly than critically damped systems.
Understanding these damping effects is essential in engineering to control vibrations and improve safety and comfort, especially in structures like tall buildings and bridges.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Damping
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In real engineering systems, damping is non-negligible. Including damping modifies the wave equation:
$$\frac{\partial^2 u}{\partial t^2} + 2\beta \frac{\partial u}{\partial t} = c^2 \frac{\partial^2 u}{\partial x^2}$$
Where \(\beta\) is the damping coefficient.
Detailed Explanation
This chunk introduces the concept of damping in engineering systems. Damping refers to the effects that reduce the amplitude of vibrations over time. In real-world scenarios, when we describe the motion of vibrating systems like strings or beams, we have to consider that energy is lost due to various factors such as air resistance or internal friction. The mathematical representation is a modification to the original wave equation by adding a damping term, represented by \(2\beta \frac{\partial u}{\partial t}\), where \(\beta\) is a constant that quantifies how much damping is present.
Examples & Analogies
Imagine a swing in a park. When you push it gently, it continues swinging back and forth. However, if you stop pushing, it slowly comes to a halt due to friction with the air and the supports. This slowing down is a form of damping, just like how structural components in buildings experience reduced vibrations due to damping devices.
Types of Damping
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Underdamped Systems: Oscillate and gradually decay.
• Critically Damped: Return to rest as quickly as possible without oscillating.
• Overdamped: Return to rest slowly without oscillating.
Detailed Explanation
This chunk describes the three primary types of damping that can occur in physical systems:
1. Underdamped Systems: These systems experience oscillations that gradually reduce in amplitude over time, meaning they continue to vibrate before coming to a rest.
2. Critically Damped Systems: In these systems, the damping is just right so that they do not oscillate at all but return to their rest position in the shortest amount of time.
3. Overdamped Systems: These systems return to rest but do so slowly and without oscillating. The system is heavily damped, which results in longer return times and no oscillatory behavior.
Examples & Analogies
Think of a car's suspension system. When you hit a bump (like a pothole), an underdamped system would bounce up and down a few times before settling. A critically damped system would smooth out the bounce and quickly stop moving, providing a comfortable ride. An overdamped system would be too stiff, leading to a very slow return to a steady position, potentially making for a bumpy ride even after the bump.
Importance of Damping in Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Damping helps control vibrations and improve structural comfort and safety (e.g., damping devices in tall buildings and bridges).
Detailed Explanation
This chunk emphasizes why damping is crucial in engineering applications. Properly designed damping devices, such as shock absorbers in tall buildings or vibration dampers in bridges, reduce the amplitude of vibrations caused by external forces such as wind or earthquakes. This improvement in vibration control enhances safety, comfort, and the longevity of structures, making them more resilient to dynamic loads.
Examples & Analogies
Consider a tall skyscraper in a windy city. Without damping, strong winds could cause the building to sway significantly, making people feel uneasy inside. Engineers use dampers, which act like giant shock absorbers, to limit this movement. It's like how a soft-ride car suspension system smoothens out the bumps on the road, ensuring a comfortable and safe journey.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Damping: Refers to the process of reducing vibrations in mechanical systems.
-
Underdamped Systems: Systems that oscillate with a gradually decreasing amplitude.
-
Critically Damped Systems: Systems that return to rest quickly without oscillating.
-
Overdamped Systems: Systems that return to rest slowly without oscillating.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Tall buildings employ damping systems to reduce oscillations caused by wind or seismic activities.
-
Suspension bridges utilize damping to control vibrations from traffic and wind loading.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
For damping in a swing, feel the gentle cling; underdamped sway, critics keep at bay.
📖 Fascinating Stories
-
Imagine a tall building during an earthquake; the dampers act like damp towels soaking up vibrations, leaving the residents snug and safe.
🎯 Super Acronyms
DUC
- Damping
- Underdamped
- Critically
- Overdamped - Remember the order of types.
D.U.C. - Damping, Under, Critically, Over.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Damping
Definition:
The effect of reducing the amplitude of vibrations over time in a mechanical system.
-
Term: Underdamped
Definition:
A type of damping where the system oscillates with gradually decreasing amplitude.
-
Term: Critically Damped
Definition:
A type of damping that returns a system to equilibrium as quickly as possible without oscillating.
-
Term: Overdamped
Definition:
A type of damping where the system returns to equilibrium without oscillating but takes longer compared to critically damped systems.
-
Term: Damping Coefficient (β)
Definition:
A parameter that characterizes the amount of damping in a vibrating system.