Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Vibrating Strings
Unlock Audio Lesson
Welcome, everyone! Today we're diving into the world of vibrating strings and the wave equation. Can anyone tell me what the fundamental assumptions are for modeling a vibrating string?
I think the string needs to be stretched tightly and have fixed ends.
Exactly! The string is modeled as perfectly flexible and tightly stretched between two fixed ends. What else do we need to consider?
The tension must stay constant while the string vibrates.
Correct! And we also assume that it only moves in a single plane and has uniform linear density. We neglect damping effects to simplify our model.
What does ignoring damping mean for our model?
Good question! Not considering damping means our solutions will not account for energy loss due to factors like air resistance or friction, simplifying our analysis.
Let's summarize: We model a vibrating string with fixed ends, consistent tension, and assume small displacements. Remember, the acronym 'FCTDS' can help you recall these assumptions: Flexibility, Constant tension, Two ends fixed, Displacement small.
Derivation of the Wave Equation
Unlock Audio Lesson
Now, let's derive the wave equation. Who can remind me what an important principle we use for this derivation?
Newton’s second law!
That's right! We'll analyze a small segment of the string using that principle. Can anyone explain how we do that?
We consider the forces acting on the segment and set the net force equal to mass times acceleration.
"Perfect! This leads us to the important equation:
Boundary and Initial Conditions
Unlock Audio Lesson
Let’s talk about boundary and initial conditions. Why are these important when we solve the wave equation?
They help us get a unique solution to the wave equation.
"Exactly! For a vibrating string fixed at both ends, we set boundary conditions like:
Methods of Solution
Unlock Audio Lesson
Now, let's explore how to solve the wave equation using the method of separation of variables. Can anyone describe how we start this process?
We assume a solution in the form of a product of two functions, one in x and one in t.
"Exactly! We can write the solution as:
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we derive the wave equation for a vibrating string under specific assumptions, analyze the mathematical properties, and identify solution techniques based on boundary and initial conditions. The implications for civil engineering applications are also discussed, highlighting the importance of this model in understanding vibration behavior in structures.
Detailed
Detailed Summary
This section focuses on the modeling of a vibrating string using the wave equation, a second-order partial differential equation crucial to engineering applications.
Key Points:
- Assumptions for the Vibrating String Model:
- The string is flexible and fixed at both ends.
- Motion is restricted to a single plane and small transverse displacements are considered.
- The string has uniform linear density and constant tension throughout.
- Damping effects are ignored for simplification.
- Derivation of the Wave Equation: We analyze a segment of the string and apply Newton's second law to derive the one-dimensional wave equation:
$$ \frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partial x^2}, $$
where c = \sqrt{\frac{T}{\rho}} is the wave speed.
- Boundary and Initial Conditions: Proper conditions are necessary to solve the wave equation uniquely. For a string fixed at both ends, the boundary conditions are:
$$ u(0,t) = 0, \quad u(L,t) = 0 $$
and initial conditions for shape and velocity must be specified.
- Solution Techniques: We employ the method of separation of variables, resulting in ordinary differential equations. The general solution is expressed as a series involving sine and cosine functions.
- Properties of Solutions: The linearity of the wave equation allows the superposition of solutions, and we identify significant concepts such as superposition, wave propagation, and standing waves.
- Applications: The vibrating string model has vast applications in civil engineering, including analyzing vibrations in bridges, building acoustics, and earthquake engineering.
The understanding of these principles is vital for predicting and managing stress, displacement, and energy transmission in civil structures, laying the groundwork for more advanced studies involving damped and nonlinear systems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Vibrating Strings
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
One of the most important applications of partial differential equations in engineering is the modeling of physical systems involving vibrations. In structural engineering, cables, suspension bridges, and other elastic members often exhibit vibrational behavior. The classical example of such a system is the vibrating string, which is mathematically modeled using the wave equation, a second-order partial differential equation.
Detailed Explanation
This chunk introduces the concept of vibrating strings, highlighting their importance in engineering applications. It explains that many structures, including bridges and cables, experience vibrations, which can be analyzed using mathematical equations known as partial differential equations, specifically the wave equation.
Examples & Analogies
Think of a guitar string. When you pluck it, it vibrates producing sound. This is a practical example of how vibrating strings are used in music, and understanding the mathematics behind these vibrations is crucial for making instruments that sound good.
Assumptions for the Vibrating String Model
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To derive the wave equation, we consider an idealized model of a vibrating string under the following assumptions:
1. The string is perfectly flexible and stretched tightly between two fixed ends.
2. The motion of the string is restricted to a single plane (e.g., vertical displacement only).
3. The tension in the string remains constant during vibration.
4. The string has uniform linear density (mass per unit length), denoted by ρ.
5. Damping effects (due to air resistance or internal friction) are neglected.
6. Transverse displacement is small, allowing linear approximations of slope.
Detailed Explanation
This chunk outlines the assumptions made to simplify the vibrating string model. Each assumption focuses on specific characteristics of the string, such as its flexibility and how it vibrates. For example, saying that the string has uniform linear density means that its mass is evenly distributed along its length, which simplifies calculations.
Examples & Analogies
Imagine stretching a rubber band between two points. If you pluck it, it vibrates. Assuming it remains perfectly stretched and does not sag is similar to the assumptions made in the model. It allows us to focus on how it vibrates without the complexity of other factors.
Derivation of the One-Dimensional Wave Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
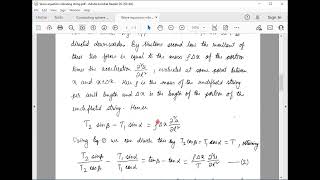
Let the string extend from x=0 to x=L, and let u(x,t) denote the transverse displacement at position x and time t. Consider a small element of the string between x and x+∆x. Let the tension at position x be T, and the angles made by the string with the horizontal at x and x+∆x be θ and θ+∆θ, respectively. Using Newton’s second law in the vertical direction:
∂²u/∂t² (Net vertical force) = ρ∆x
T sin(θ + ∆θ) − T sin(θ) ≈ T (x + ∆x) − T (x)
This leads to the wave equation: ∂²u/∂t² = c² ∂²u/∂x², where c = √(T/ρ) is the wave speed.
Detailed Explanation
This chunk describes how the wave equation is derived starting from basic physical principles. By analyzing a small segment of the string and applying Newton’s second law, we establish the relationship between the forces acting on the string and its acceleration, leading us to the one-dimensional wave equation, which describes how waves propagate along the string.
Examples & Analogies
Imagine shaking a jump rope. The tension is like the force you apply to create a wave. The movement of the rope as you shake it can be described by the wave equation, which shows how waves travel along the length of the rope.
Boundary and Initial Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For a well-posed problem, the wave equation must be accompanied by appropriate boundary and initial conditions. Boundary Conditions (BC): For a string fixed at both ends:
- u(0, t) = 0, u(L, t) = 0 for all t ≥ 0
Initial Conditions (IC): Let the initial shape and velocity of the string be given by:
- u(x, 0) = f(x), ∂u/∂t(x, 0) = g(x) for 0 ≤ x ≤ L.
Detailed Explanation
In this chunk, we learn that solving our wave equation requires specific conditions to be defined. Boundary conditions specify the behavior of the string at its ends, while initial conditions establish how the string is positioned and moving at time zero. This ensures that our solutions are relevant to the actual physical problem.
Examples & Analogies
Consider tuning a piano. The strings are fixed at both ends, just like our boundary conditions. The initial sound each string makes when struck is like the initial conditions, providing the starting point for the musical note produced.
Method of Separation of Variables
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To solve the wave equation, we use the method of separation of variables. Assume a solution of the form: u(x, t) = X(x)T(t). Substitute into the wave equation:
T’’(t) / T(t) = c² X’’(x) / X(x) = -λ.
We now solve two ordinary differential equations:
Detailed Explanation
This chunk introduces the method of separation of variables, which allows us to break down the complicated wave equation into simpler parts. By assuming that the solution can be written as a product of two functions, one depending on space and the other on time, we can generate two ordinary differential equations to solve independently.
Examples & Analogies
Think of separating ingredients for a recipe—like making a salad where you mix lettuce, tomatoes, and dressing separately before combining them. In the same way, we are separating the spatial and temporal components of our wave equation before putting them together to find the complete solution.
Properties of the Solution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Superposition Principle: The linearity of the wave equation allows superposition of solutions.
• Wave Propagation: Disturbances propagate along the string with speed c, determined by tension and linear density.
• Standing Waves: The natural modes of vibration correspond to standing waves with fixed nodes and antinodes.
• Energy Conservation: In the absence of damping, total mechanical energy is conserved.
Detailed Explanation
This chunk summarizes key properties of the solutions derived from the wave equation. These properties include how waves can overlap (superposition principle), the speed at which they travel, the formation of standing waves, and the principle of energy conservation in an ideal system.
Examples & Analogies
Think of fireworks being set off in the sky. Each explosion is a wave that propagates from the center outward. If multiple fireworks go off, their effects can combine in dazzling displays (superposition). The energy generated remains constant until the fireworks fade, illustrating conservation of energy.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Wave Equation: A mathematical description of wave motion forming the basis for modeling vibrations in strings.
-
Boundary Conditions: Conditions necessary for solving differential equations, applicable at the ends of vibrating strings.
-
Initial Conditions: Specifications of the system's state at the start, crucial for determining unique solutions.
-
Separation of Variables: A strategic approach to simplify and solve partial differential equations.
-
Superposition Principle: The concept that allows for the combination of multiple solutions in linear systems.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A guitar string can be modeled as a vibrating string, allowing us to analyze how vibrations propagate when plucked.
-
Suspension bridge cables experience vibrations due to wind, which can be modeled using the wave equation.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
For vibrating strings taut and tight, the equations of motion bring delight.
📖 Fascinating Stories
-
Imagine a guitar string, strummed gently. At each end, it's fixed; in the center, it dances. The tension guides its movement, echoing waves of sound.
🧠 Other Memory Gems
-
Remember 'BIC' for Boundary and Initial Conditions that help us model vibrations correctly.
🎯 Super Acronyms
Use 'FCTDS' to remember the assumptions
- Flexibility
- Constant tension
- Two ends fixed
- Displacement small.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Vibrating String
Definition:
A flexible medium that transmits vibrations along its length when disturbed.
-
Term: Wave Equation
Definition:
A second-order partial differential equation that describes the propagation of waves.
-
Term: Boundary Conditions
Definition:
Conditions that specify the behavior of solutions at the boundaries of the domain.
-
Term: Initial Conditions
Definition:
Conditions that specify the behavior of solutions at the initial moment in time.
-
Term: Superposition Principle
Definition:
The principle that allows the total response of a linear system to be expressed as the sum of individual responses.
-
Term: Eigenvalues
Definition:
Values that characterize the natural frequencies of a system.
-
Term: Separation of Variables
Definition:
A mathematical method used to solve partial differential equations by separating variables.