Finite Element Method (FEM)
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to FEM
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Welcome everyone! Today, we're going to explore the Finite Element Method, or FEM. Can anyone tell me what they think FEM is used for in engineering?

Is it about breaking things into smaller parts to analyze them?

Exactly, Student_1! FEM divides a large problem into smaller, simpler parts called 'elements.' This allows engineers to analyze complex structures effectively. Remember the acronym 'FEM' stands for 'Finite Element Method.'

Why do we need to use FEM instead of traditional methods?

Great question, Student_2! Traditional analytical methods can be impractical for complex geometries. FEM is more flexible and can handle varying material properties and boundary conditions efficiently.

Can we use FEM for any type of engineering problem?

Generally, yes! FEM is widely used in civil, mechanical, and even aerospace engineering to solve problems involving vibrations, heat transfer, and fluid dynamics.

So, it’s like a powerful tool for simulations?

Absolutely, Student_4! It's essential for predicting how structures will behave under loads.

To sum up, FEM is about dividing complex systems into manageable parts for analysis. It’s flexible, applicable across various fields, and essential for accurate engineering predictions.
Applications of FEM
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we understand FEM, let's discuss its applications. Can anyone give me an example of where FEM might be used?

It could be used for analyzing a bridge?

Exactly! In bridge engineering, FEM helps simulate how different forces affect the structure, essential for safety and design.

What about in buildings?

Yes, Student_2! In buildings, FEM is used to analyze vibrations caused by wind or earthquakes, ensuring structures can withstand these forces. What other areas can we think of?

Maybe in software simulations for car crash tests?

Great point! FEM plays a crucial role in automotive engineering as well, helping predict how cars behave in crashes, leading to better safety designs.

So, the simulations help create safer designs?

Correct! By using FEM, engineers can optimize designs to enhance safety and performance without having to build physical prototypes. This saves time and resources.

In summary, FEM is applied in various fields, including civil engineering, automotive, and even aerospace, making it a vital tool for modern engineering challenges.
Advantages and Limitations of FEM
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's talk about the advantages of using FEM. What do you think they might be?

I guess it’s more accurate than other methods?

That's right, Student_1! FEM provides accurate solutions for complex problems, which is one of its main advantages. It can also handle nonlinear effects and varying material properties.

Are there any downsides to using FEM?

Good observation, Student_2! While FEM is powerful, it can be computationally intensive and requires significant data to set up correctly. Adequate training is also necessary for effective application.

So we need to be careful with our inputs, right?

Exactly! Garbage in, garbage out. If the input parameters are incorrect, the results can be misleading.

Is there a way to check if our results are accurate?

Certainly! Engineers often compare FEM results with analytical solutions for simple cases or conduct experimental validation to ensure accuracy.

To recap, FEM is advantageous for its accuracy and versatility but comes with challenges such as computational demands and the need for precise input data.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
FEM is essential in structural analysis, allowing engineers to solve complex problems associated with partial differential equations and mechanical behavior. It breaks down structures into simpler, piecewise linear elements for efficient computational analysis.
Detailed
Finite Element Method (FEM)
The Finite Element Method (FEM) is a powerful numerical method used for solving partial differential equations, especially in structural engineering. It operates by dividing a complex structure into discrete sections or elements, allowing for the management of intricate geometries and varied material properties. FEM is particularly valuable in civil and mechanical engineering, as it provides accurate solutions for stress, strain, and deformation analyses under various loading conditions and constraints. Standard civil engineering software such as ANSYS and ABAQUS are commonly used to implement FEM for various applications, making it a cornerstone in modern engineering practices.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Finite Element Method
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Approximates solution using piecewise polynomials (basis functions).
Detailed Explanation
The Finite Element Method (FEM) is a numerical technique used to find approximate solutions to complex engineering problems. It works by dividing a large problem into smaller, simpler parts known as elements. These elements are connected at points called nodes. By approximating the solution within each element using simple polynomial functions, we can create a comprehensive approximation of the entire structure or system. This technique is particularly useful for analyzing complex geometries and varying boundary conditions that are often encountered in structural engineering.
Examples & Analogies
Imagine trying to solve a complicated jigsaw puzzle with irregularly shaped pieces. Instead of trying to fit the whole puzzle together at once (which can be daunting), you can start by solving smaller sections of the puzzle, focusing on fitting those pieces together correctly. Once the smaller sections are completed, you then link them together to see the full picture. Similarly, FEM allows engineers to approach complex problems in manageable sections.
Application in Engineering Software
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Efficient for complex structures and boundary conditions.
• Standard in commercial civil engineering software (e.g., ANSYS, ABAQUS).
Detailed Explanation
FEM is highly efficient for analyzing structures with complex shapes and loads. It can easily handle varying material properties and boundary conditions, which are common in real-world applications. As a result, many civil engineering software packages, such as ANSYS and ABAQUS, incorporate FEM techniques. Engineers use these tools to simulate real-life behavior of structures under various conditions, allowing for better understanding, design optimization, and safety evaluations without conducting expensive physical experiments.
Examples & Analogies
Think of a video game that simulates a physics environment. The game developers use complex algorithms to model how objects will behave when interacted with forces like gravity or collisions. By applying these simulations, they can predict how the game will play and adjust elements to improve user experience. Similarly, with FEM in engineering software, engineers can simulate real-life scenarios of structures to predict how they will perform under stress or different environmental factors.
Key Concepts
-
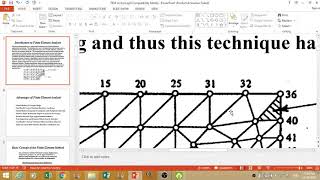
Discretization: The process of breaking a continuous structure into small elements for analysis.
-
Mesh: The network of elements created for FEM that defines the geometry of the problem.
-
Boundary Conditions: The constraints applied to the edges or surfaces of the elements.
-
Solver: The tool or software used to calculate the approximate solution using FEM.
Examples & Applications
Analyzing stress distribution in a bridge under wind load using FEM.
Simulating thermal effects in a building during fire exposure with FEM.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
FEM breaks it down, into pieces so neat, solving complex problems, can't be beat!
Stories
Imagine a magician who splits a big monster into tiny puppets for easier control. That's like FEM making sense of the chaotic structures in engineering.
Memory Tools
Please Make Better Solutions (P.M.B.S) to remember the FEM process: 'Please' - Problem Identification, 'Make' - Mesh Generation, 'Better' - Boundary Conditions Application, 'Solutions' - Solving the Equations.
Acronyms
F.E.M.
Finite Elements Manage complexity.
Flash Cards
Glossary
- Finite Element Method (FEM)
A numerical technique to obtain approximate solutions of partial differential equations by breaking down complex structures into discrete elements.
- Element
A basic unit in the FEM that represents a small portion of a larger structure.
- Boundary Condition
Constraints that define how the edges and surfaces of a structure interact with the environment.
- Mesh
The collection of elements that make up the model in FEM.
- Solver
Software or algorithm used to find approximate solutions using FEM.
Reference links
Supplementary resources to enhance your learning experience.
