Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Euler's Method
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to discuss Euler's Method, a simple yet effective numerical way to solve ordinary differential equations. Can anyone tell me why we might need a numerical method?
We need numerical methods when we can't solve equations analytically.
Exactly! Now, what do you think are the main advantages of using Euler's Method?
I think it’s easy to understand and implement.
Correct! So, its simplicity is a big advantage. What about computational cost?
It’s less expensive, so we can use it on simple models!
Great! Now let's consider its drawbacks. Why might someone be cautious about using Euler's Method?
It’s not very accurate, especially with larger step sizes.
Exactly! And what about instability in certain equations?
Yeah, it can fail if the equation is stiff or the step size is too big.
Excellent summary! Remember, while Euler's Method is useful due to its simplicity and low cost, it has significant limitations in accuracy and stability.
Exploring Accuracy and Stability
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we understand the advantages and disadvantages, let’s dive deeper into accuracy. What does it mean for a method to be only first-order?
It means the errors decrease linearly with the step size.
Exactly! If we reduce the step size, how does it affect our accuracy?
The error will decrease, but not as quickly as more advanced methods!
Correct. Now, can anyone elaborate on stability and why that’s critical for certain equations?
Stability is crucial for stiff equations because if a method isn't stable, the errors could grow dramatically.
Right! If we apply Euler's Method to stiff equations with large steps, we risk getting results that diverge from the actual solution. This is a significant limitation!
So, it’s essential to choose the right method depending on what we’re solving!
Exactly! That's a fundamental aspect of numerical analysis.
Practical Applications and Decision Making
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
In practice, when would you consider using Euler's Method instead of more advanced techniques?
For quick approximations where high precision isn't required?
Exactly! Sufficient for simple models, but what about the computational expense aspect?
It would be good if we need faster results without much complex computation!
Correct! So remember: When solving simple problems or when computational resources are limited, Euler’s Method is often a good choice. Can anyone summarize why we must keep its limitations in mind?
Because even a small error can propagate, leading to very inaccurate results.
Great recap! Keep in mind that while Euler’s Method is incredibly useful, understanding when and how to use it is vital to accuracy.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Euler's Method is highly regarded for its simplicity and low computational expense, making it easy to implement. However, it suffers from low accuracy and stability issues, especially with stiff equations or larger step sizes, which restricts its applicability in many complex scenarios.
Detailed
Advantages and Disadvantages of Euler's Method
Euler's Method is one of the simplest and most straightforward numerical techniques used to solve ordinary differential equations (ODEs). While it boasts significant advantages, it also presents notable disadvantages that should be considered for effective application. In this section, we delve into both aspects of Euler's Method:
Advantages
- Simplicity: Euler's Method is very easy to implement and understand, making it accessible for beginners.
- Computational Inexpensiveness: The method requires relatively less computational power compared to more complex methods like Runge-Kutta, allowing it to be used for simple models effectively.
Disadvantages
- Low Accuracy: Euler's Method is only a first-order technique. This means that as the step size decreases, the error decreases linearly, leading to potentially inaccurate results if the step is too large.
- Instability: The method may produce inaccurate or unstable results when applied to stiff equations or when larger step sizes are utilized. This limitation greatly hinders its effectiveness in more complex systems.
Understanding these advantages and disadvantages is crucial for selecting appropriate numerical methods for solving ODEs.
Youtube Videos
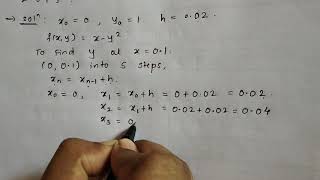
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Advantages of Euler’s Method
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Very simple to implement and understand.
- Computationally inexpensive.
Detailed Explanation
Euler’s method is known for its ease of use. This means that students and practitioners can quickly learn how to apply it without needing extensive background knowledge in numerical methods or mathematics. Its basic procedure involves simple calculations that can be performed by hand or using minimal computational resources, which makes it ideal for educational purposes and quick estimations.
Examples & Analogies
Think of Euler's method as a basic recipe for making a simple cake. The ingredients are few, and the steps are straightforward. You can just mix them together without worrying about advanced cooking techniques, making it accessible to anyone who wants to bake.
Disadvantages of Euler’s Method
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Low accuracy: Euler’s method is only a first-order method, meaning the error decreases linearly with the step size h.
- Instability: For stiff equations or large step sizes, Euler’s method may produce inaccurate or unstable results.
Detailed Explanation
While Euler's method is simple and easy to implement, it has significant limitations regarding accuracy. Being a first-order method, the rate at which errors decrease is quite slow; as you reduce the step size, the accuracy improves linearly, which may not be sufficient for more complex equations. Additionally, the method can become unstable, particularly with stiff equations, leading to results that are not only inaccurate but also diverge from the true solution as the calculations progress.
Examples & Analogies
Consider using a very basic tool, like a hand saw, to cut a piece of wood. While it can get the job done, if you're aiming for precision, you might end up with rough edges and uneven cuts. Similarly, Euler's method can produce rough approximations and may not be suitable for all types of 'cuts' in mathematical modeling, particularly where more complicated phenomena are involved.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Simplicity: Euler's Method is easy to implement and understand.
-
Low computational expense: It requires fewer resources compared to advanced methods.
-
Low accuracy: The accuracy improves linearly with smaller step sizes, but is generally low.
-
Instability: Euler’s Method can lead to inaccurate results in stiff equations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Euler's Method is often used to approximate solutions to population growth equations where high precision is not crucial.
-
In engineering, Euler's Method might be employed to model simple dynamic systems like a falling object under gravity.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Euler’s Method's easy to see, but watch your step size, or errors will flee!
📖 Fascinating Stories
-
Once upon a time, there was a method called Euler who loved to simplify calculations. However, he learned that hurrying with large steps could lead to a mess, teaching a lesson that precision mattered.
🧠 Other Memory Gems
-
Remember S.L.I. for Euler's disadvantages: S for Stability issues, L for Low accuracy, I for Implementation simplicity.
🎯 Super Acronyms
Use E.A.S.Y. to recall Euler's Method
- E: for Easy
- A: for Affordable
- S: for Simple
- Y: for Yielding low accuracy.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Ordinary Differential Equation (ODE)
Definition:
An equation involving functions of a single variable and their derivatives.
-
Term: Computational expense
Definition:
The amount of computational resources (time, memory, etc.) required to perform a mathematical operation.
-
Term: Stability
Definition:
The property of a numerical method to produce bounded results even when applied to stiff problems or equations.