Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Euler's Method
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will explore Euler's method for solving ODEs. Can anyone tell me what ODE stands for?
Ordinary Differential Equation.
Correct! Euler's method is one of the simplest ways to approximate solutions for ODEs. It uses a first-order approximation and is very straightforward to implement.
What is the main formula for Euler's method?
The formula is y_{n+1} = y_n + h imes f(t_n, y_n), where h is the step size. Remember, we use this formula iteratively to find successive values.
What are some advantages and disadvantages of using Euler's method?
Great question! The advantages include its simplicity and low computational cost. However, it has low accuracy and may lead to instability, particularly with stiff equations.
So, itβs easy to use but not very accurate?
Exactly! Remember, itβs a trade-off between simplicity and accuracy. In summary, while itβs a basic method, it can be insufficient for complex problems.
Runge-Kutta Methods
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's compare this to the Runge-Kutta methods, specifically RK4. Can someone explain what RK4 stands for?
It stands for the fourth-order Runge-Kutta method.
Fantastic! This method is more accurate than Euler's method because it uses multiple intermediate slopes. Who can tell me how many slopes RK4 uses?
Four slopes: k1, k2, k3, and k4.
Correct! The final estimate of the next value is a weighted average of these slopes. This gives it a much smaller error compared to the first-order method.
What about the computational cost compared to Euler's?
Good question! RK4 requires more calculations, specifically four evaluations per step, making it more computationally expensive, but the increased accuracy often justifies the cost.
So is it better for all ODEs?
Not necessarily; RK4 can struggle with stiff equations. Be sure to choose the method based on the problem characteristics!
Multistep Methods
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Moving on, letβs discuss multistep methods, including the Adams-Bashforth and Adams-Moulton methods. Who can tell me the main difference between them?
Adams-Bashforth is an explicit method while Adams-Moulton is implicit.
Exactly! The Adams-Bashforth methods compute the next value using previous values only, while Adams-Moulton methods consider both current and previous values, enhancing stability.
What does it mean for a method to be implicit?
Good question! Implicit methods, like Adams-Moulton, often require solving equations for the next value, which increases complexity. However, they tend to be more stable, especially for stiff equations.
So is an implicit method always better?
Not always. It depends on the problem. They can be computationally expensive due to the need for solving systems of equations. Always assess your problem before choosing a method!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the comparison of various numerical methods for solving ODEs, particularly focusing on Euler's Method, Runge-Kutta Methods, and Multistep Methods (Adams-Bashforth and Adams-Moulton). Each method is evaluated based on its order of accuracy, computational cost, advantages, and challenges, providing insight into when to use each approach.
Detailed
Comparison of Numerical Methods for ODEs
This section presents a comprehensive comparison of three numerical methods for solving Ordinary Differential Equations (ODEs): Euler's method, Runge-Kutta methods, and Multistep methods. Understanding the strengths and weaknesses of each method is crucial for selecting the appropriate technique for a given problem.
1. Euler's Method
- Order of Accuracy: First-order method (O(h)).
- Computational Cost: Low; only one function evaluation per step.
- Advantages: Very simple to implement and computationally inexpensive.
- Disadvantages: Low accuracy and may suffer from instability, especially with stiff equations.
2. Runge-Kutta Methods
- Order of Accuracy: Fourth-order method (O(h^5) error).
- Computational Cost: Moderate; requires four function evaluations per step.
- Advantages: Better accuracy than Euler's method with relatively small computational overhead.
- Disadvantages: More expensive computationally than Eulerβs method and may still struggle with stiff equations.
3. Multistep Methods
a. Adams-Bashforth (Explicit Multistep)
- Order of Accuracy: Varies based on the number of steps used.
- Computational Cost: Moderate; uses multiple prior function evaluations.
- Advantages: More accurate than single-step methods for the same number of function evaluations.
- Disadvantages: Requires knowledge of previous function values, which may not always be accessible.
b. Adams-Moulton (Implicit Multistep)
- Order of Accuracy: Varies based on the number of steps used.
- Computational Cost: High; involves solving a system of equations at each step.
- Advantages: Very stable and suitable for stiff equations.
- Disadvantages: Higher computational cost due to the need for solving nonlinear systems.
This comparison illustrates the trade-offs between simplicity and accuracy, guiding the choice of method based on the specifics of the problem.
Youtube Videos
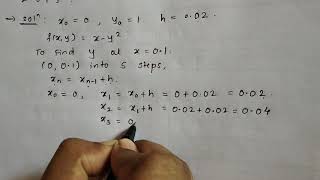
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Comparison Table of Numerical Methods
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Method Order of Step Computational Advantages Disadvantages
Accuracy Type Cost
Euler's First-order Single-ste Low Simple and Slow
Method p easy to convergence,
inaccurate
Runge-Ku Fourth-order Single-ste Moderate Accurate, fast Computationally
tta (RK4) p convergence expensive
Adams-Ba Varies Multistep Moderate Faster than Requires
shforth (depends on (explicit) single-step previous points
methods
Adams-M Varies Multistep High Stable, good Computationally
oulton (depends on (implicit) for stiff ODEs expensive
terms of
steps used)
Detailed Explanation
This table summarizes the four main numerical methods used to solve ordinary differential equations (ODEs): Euler's Method, Runge-Kutta (RK4) methods, Adams-Bashforth methods, and Adams-Moulton methods. Each method is compared across several criteria:
- Order of Accuracy: This indicates how the error decreases as the step size is reduced. Euler's method is a first-order method, while RK4 and Adams methods can be higher order, leading to lower errors for smaller step sizes.
- Type: This classification indicates whether the method is single-step or multistep. Single-step methods use only the latest data point to compute the next value, while multistep methods use multiple previous values, which can make them more efficient.
- Computational Cost: This represents how much computational resource is required for each method. For example, Eulerβs method is low cost, but more accurate methods like RK4 are computationally more expensive due to the calculations involved in determining intermediate values.
- Advantages and Disadvantages: Each method is evaluated based on its pros and cons, such as ease of implementation, speed or stability, and accuracy. Euler's method is simple but has slow convergence, while RK4 is more accurate but requires more computation. Multistep methods, while more efficient, often need previous steps, which could be a limitation.
Examples & Analogies
Think of these methods as different vehicles for navigating a city. Euler's Method is like a simple bicycleβit's easy to ride (easy to implement), but you might not get far fast (slow convergence) and can easily get lost (low accuracy). The Runge-Kutta method can be compared to a car; it's faster and can navigate more complex routes efficiently (higher accuracy and acceptable computational cost), but it requires more fuel (computational power). Multistep methods are like busesβthey can carry many passengers (use previous points for accuracy) but require a schedule (previous steps) to operate effectively.
Euler's Method
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
First-order Single-ste Low Simple and Slow
Method p easy to convergence,
inaccurate
Detailed Explanation
Euler's Method is the most basic technique for solving ordinary differential equations. It is a first-order method, meaning that its accuracy increases linearly as the step size decreases. The main advantage is its ease of implementation and low computational cost, which makes it attractive for simple problems. However, it struggles with accuracy, producing significant errors unless a small step size is used, which can increase computation time. Therefore, while Euler's Method is effective for simple cases, it is not suitable for all scenarios, especially where high accuracy is required.
Examples & Analogies
Imagine a student who is solving math problems. If the student uses a simple calculator to get answers, and they don't check their work carefully, they might make mistakes. You can think of Euler's Method as that studentβit's quick and easy to use (like a calculator), but it often leads to errors unless they're very careful (small step size increases accuracy). For tougher problems, the student may need to use more advanced solving techniques that take longer but yield better answers.
Runge-Kutta (RK4) Method
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Fourth-order Single-ste Moderate Accurate, fast Computationally expensive
Detailed Explanation
The Runge-Kutta method, especially the fourth-order variant (RK4), is widely used in solving ODEs due to its balance of accuracy and computational cost. It calculates several intermediate slope estimates for each step and combines them to produce a single, more accurate approximation. This results in better accuracy compared to Euler's Method, and it remains computationally feasible for many applications, making it a popular choice. However, it is more computationally demanding than simple methods like Eulerβs, requiring multiple calculations per iteration.
Examples & Analogies
Think of the RK4 method like using a GPS system for navigation. Just as a GPS provides several route options and recalibrates as you drive to ensure you stay on course, RK4 calculates several estimates before providing a final value for a solution, thus ensuring accuracy. While the GPS might require more resources, such as a charged battery or cellular data, it generally leads you to your destination more accurately.
Adams-Bashforth Methods
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Varies Multistep Moderate Faster than Requires previous points
(explicit) single-step methods
Detailed Explanation
The Adams-Bashforth methods are a class of explicit multistep methods that leverage multiple prior values of the solution for better accuracy and efficiency. Since they use the previous steps to inform the next calculation, they can be quicker than single-step methods for the same number of function evaluations. However, this reliance on previous values can also limit their use, especially if early points are not available or if the system is dynamically changing.
Examples & Analogies
Imagine trying to predict someone's movement in a game by remembering where they were a few seconds ago; thatβs like the Adams-Bashforth methods, which rely on past data to predict future states. If you are quick and can remember lots of past positions, your predictions become much faster and more accurate (faster than single-step methods). But if you forget where they were, you can miss calculating their movement correctly.
Adams-Moulton Methods
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Varies Multistep High Stable, good Computationally for stiff ODEs
(implicit) expensive
Detailed Explanation
The Adams-Moulton methods are implicit multistep techniques that, similarly to Adams-Bashforth methods, utilize information from multiple prior steps. These methods tend to be more stable and accurate, particularly in cases involving stiff ordinary differential equations (ODEs), where the solution may change rapidly. While their higher stability is a significant advantage, the computational burden increases notably since implicit methods typically require solving a system of equations at each step.
Examples & Analogies
Consider Adams-Moulton methods like a weather forecasting system that uses both current and past data to predict tomorrow's weather. While it may take more processing power to run the simulations (higher computational cost), it provides reliable forecasts even in unpredictable conditions (stable and good for stiff ODEs). This balanced approach can lead to accurate predictions, even if it requires more resources to achieve that accuracy.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Euler's Method: A simple, first-order method for approximating ODE solutions.
-
Runge-Kutta Methods: A more accurate, higher-order method for solving ODEs.
-
Multistep Methods: Use multiple past solutions to estimate the next value, enhancing efficiency.
-
Adams-Bashforth: An explicit method utilizing previous values for estimation.
-
Adams-Moulton: An implicit method that combines current and prior values for stable solutions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using Euler's Method to approximate y(t) for dy/dt = y with an initial condition y(0)=1.
-
Applying the Runge-Kutta method to find the solution for dy/dt = cos(t) with y(0)=0.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Euler's method is so neat, it can't be beat, but low accuracy is its defeat.
π Fascinating Stories
-
Imagine a student named Euler who dreamt of solving equations. He crafted a neat method to hop along the solutions, but sometimes he stumbled on steep cliffs, realizing his method needed a little more depth.
π§ Other Memory Gems
-
Remember the acronym 'RUM': Runge-Kutta for increased accuracy, Use multistep for efficiency, Maintain stability with implicit methods.
π― Super Acronyms
EASY β Euler, Adams, Stability, Yield high accuracy in multistep methods.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Ordinary Differential Equation (ODE)
Definition:
An equation involving functions of a single variable and their derivatives.
-
Term: Euler's Method
Definition:
A first-order numerical method for solving ODEs by approximating solutions using discrete steps.
-
Term: RungeKutta Methods
Definition:
A family of numerical methods for solving ODEs that provide improved accuracy over Euler's method.
-
Term: Multistep Methods
Definition:
Numerical methods that use multiple previous points to estimate the next value of a solution.
-
Term: AdamsBashforth
Definition:
An explicit multistep method that uses previous values to compute the next value.
-
Term: AdamsMoulton
Definition:
An implicit multistep method that combines information from current and previous values, improving stability.