Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Euler's Method
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we are going to explore how Euler's method works for solving ordinary differential equations. To understand this, we start with an initial condition, say y(t0)=y0. Can anyone remind me what an initial condition is?
It's the known value of the function at a particular point, right?
Exactly! Now, does anyone know what we need to do with this initial condition next?
We need to compute the derivative using the function f(t0, y0).
Correct! This derivative will guide us in updating the value of our function. Now let’s see how we use this derivative.
Applying the Euler Update Formula
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we have the derivative, we apply the Euler update formula: y(n + 1) = y(n) + h * f(t(n), y(n)). Can someone explain what each component represents?
Sure! y(n) is our current approximation, h is our step size, and f(t(n), y(n)) is the derivative.
Perfect! What happens after we calculate y(n + 1)? What do we do next, Student_4?
We repeat the process for the next approximation!
Exactly right! This iterative process allows us to move through the solution progressively.
Understanding Limitations
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
What do you all think about the advantages of Euler's method? Why is this method popular despite its limitations?
It's simple to implement and understand!
And it doesn't take too much computational power.
Good points! However, what can you say about its accuracy and stability?
It's not very accurate, especially for stiff equations or large step sizes.
Right again! Euler's method is a first-order method, meaning our error decreases linearly with the step size. Remember, with numerical methods, we balance simplicity and accuracy!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section delves into Euler's method, a foundational numerical approach to solving ordinary differential equations. Starting from an initial condition, the method computes successive approximations of the solution by iteratively applying the Euler update formula. The simplicity of the method makes it accessible, though it has limitations in accuracy and stability.
Detailed
How Euler’s Method Works
Euler's method is a straightforward numerical technique for approximating solutions to ordinary differential equations (ODEs). This section outlines the step-by-step process of implementing Euler's method, starting with an initial condition and iteratively using the derivative to update the solution. The key points include:
1. Initial Condition: Begin with a known point of the solution, represented as y(t0)=y0.
2. Compute Derivative: Find the derivative using the ODE function, f(t0, y0).
3. Euler Update Formula: Use the formula y(n+1) = y(n) + h * f(t(n), y(n)) to compute the next value iteratively.
4. Iteration: Repeat the process, feeding results into the next calculation to approximate the solution progressively over time.
Although Euler’s method is easy to implement and requires low computational resources, it is a first-order method with considerable drawbacks in terms of accuracy and stability, particularly for stiff equations or larger step sizes. This section is crucial for understanding the foundations of numerical methods before delving into more complex techniques.
Youtube Videos
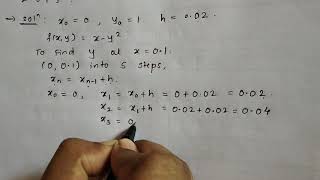
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Starting with Initial Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Start with an initial condition y(t0)=y0y(t_0) = y_0.
Detailed Explanation
To use Euler’s method, we need to begin with an initial condition, which is a known value of the function at a certain point. This initial condition is represented as y(t0) = y0 where t0 is the starting time, and y0 is the initial value of the solution. This establishes the first point of our numerical approximation.
Examples & Analogies
Think of starting a journey from a specific location. Just like you need to know your starting point (like a map pin) to determine where to go next, you need to know the initial condition to start applying Euler’s Method.
Computing the Derivative
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Compute the derivative f(t0,y0)f(t_0, y_0) using the ODE.
Detailed Explanation
Next, we compute the derivative at the initial condition. The derivative, denoted f(t0, y0), tells us how the function is changing at that specific point. This derivative is derived from the original ordinary differential equation (ODE). It provides essential information on the slope of the function at the starting point and is critical for determining how to update our solution.
Examples & Analogies
Imagine you are driving a car. Knowing how fast you are going at a particular moment (your speed) is like calculating the derivative; it tells you how your position (the function) is changing over time.
Updating the Solution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Use the Euler update formula to compute y1y_1 at the next step.
Detailed Explanation
Now, using the Euler update formula, we compute the next value of our approximation, denoted as y1. The formula is y1 = y0 + h ⋅ f(t0, y0), where h is the step size. This formula effectively takes our initial value and adds the estimated change (derived from the slope at that point) to get the next point in our approximation of the solution.
Examples & Analogies
It's like walking a certain distance based on how steep a hill is. If you know the slope of the hill (the derivative) and how far you want to walk (the step size), you can predict where you will be after that step.
Repeating the Process
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Repeat the process for each subsequent step, using the previous solution to calculate the next one.
Detailed Explanation
Once we calculate the new approximation y1, we can repeat these steps to find further points in our solution. This means calculating the new derivative with the most recent y value to update our solution continuously at each step, creating a series of approximations that together form the numerical solution to our ODE.
Examples & Analogies
Consider this like checking your GPS while driving. After each segment of your journey, you reassess your position and adjust your route accordingly to ensure you stay on track toward your destination.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Initial Condition: The starting value of the function in Euler’s method.
-
Euler Update Formula: The method for calculating the next approximation based on previous values.
-
Iterative Process: The continuous application of the update formula to approximate solutions over time.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For the ODE dy/dt = y, y(0) = 1, using h=0.1, we calculate y1 = 1 + 0.1 * 1 = 1.1.
-
Subsequently, we calculate y2 by substituting y1 back into the Euler formula.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Euler's trick, don't be sick; use f(t,y) to make y stick.
📖 Fascinating Stories
-
Imagine a tiny robot walking along a path, calculating its position based on its speed at every step. This robot uses Euler's method to navigate accurately.
🧠 Other Memory Gems
-
To remember the steps: I Compute (Initial condition), D Derivative, U Update (Euler's update), I Iterate!
🎯 Super Acronyms
ICUID
- Initial Condition
- Use Derivative
- Update Iteratively
- for Euler's Method.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Ordinary Differential Equation (ODE)
Definition:
An equation involving functions of a single variable and their derivatives used to model real-world phenomena.
-
Term: Initial Condition
Definition:
A known value of the function at a specific point, which forms the starting point for numerical methods.
-
Term: Derivative
Definition:
A measure of how a function changes as its input changes, calculated through the function f(t, y).
-
Term: Step Size (h)
Definition:
The distance between successive points in the domain used in iterative methods.
-
Term: Euler Update Formula
Definition:
The formula used to compute the next approximation in Euler's method: y(n+1) = y(n) + h * f(t(n), y(n)).