Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Euler's Method
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Welcome, everyone! Today we will learn about Euler's Method, a fundamental technique to solve ordinary differential equations. Has anyone heard of it before?
I think I've seen it mentioned briefly in my math class, but I don't understand it fully.
That's perfectly okay! Euler's Method is all about approximating solutions by taking small steps. Imagine walking along a path instead of jumping directly to your destination. Would you feel more secure walking step by step?
So, itβs like taking calculated small moves instead of a leap. How do we know how big those steps should be?
Great question! The size of the step is defined by h. Choosing a smaller h gives you a more accurate approximation. For example, if h is 0.1, we calculate the next y value using the formula: y_{n+1} = y_n + h * f(t_n, y_n). Letβs remember this formula; we can use the acronym βy=h*fβ!
Thatβs useful! But I am curious, what if h is too large?
Excellent curiosity! If h is too large, we might make large errors, leading to unstable results. That's one of the disadvantages of Eulerβs method. Now, let's move on and see how the method works practically.
The Formula in Euler's Method
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, letβs delve deeper into the formula itself: y_{n+1} = y_n + h * f(t_n, y_n). Each component plays a vital role, donβt you think?
Yes! I see that y_n is our current value and f(t_n, y_n) is the derivative. But what does 'f' actually represent?
Great observation! The function f represents the derivative of y with respect to t. It's essentially telling us how y is changing at that point, which we use to update our next y value.
So each step gives us a little more insight into how y behaves over time?
Exactly! By iterating this process, we build a curve of approximations. Remember, thoughβlower step sizes generally help improve accuracy but require more calculations. That's why finding a balance is essential!
Got it! Itβs all about maintaining the right pace.
Advantages and Disadvantages of Euler's Method
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
So far, we have discussed Euler's method and how to use its formula. Now let's look at some of its advantages and disadvantages. Would someone like to start with the pros?
Iβd say itβs simple and easy to implement. That makes it accessible for many!
Exactly! And computationally inexpensive too. Anyone want to mention downsides?
Well, I learned that it has low accuracy since itβs a first-order method. So, as we reduce the step size, we can only get precision to a point.
That's right! As you reduce step size, the error decreases linearly. Furthermore, it's less stable for stiff equations. So, while Eulerβs method is a great start, more complex methods may be necessary for challenging problems.
So itβs a trade-off between simplicity and accuracy?
Absolutely! Remember this balance as we proceed to learn about the Runge-Kutta methods, which tackle these issues effectively.
Example Application of Euler's Method
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's apply Euler's method using an example! Consider the ODE: dy/dt = y and our initial condition y(0) = 1 with a step size of h = 0.1. Who can tell me the first update?
Using our formula, we get y_{1} = y_{0} + h * f(t_{0}, y_{0}) = 1 + 0.1 * 1 = 1.1!
Exactly! And what would be next? We continue using the value just calculated, right?
Yes! So for y_2, it would be y_{2} = 1.1 + 0.1 * 1.1! Itβs around 1.21, I think.
Right! And it iterates from there. Each step builds upon the previous. This is a neat way to visualize the approximation process and see how quickly values change.
This makes it much clearer! I can see how the iterative nature helps build a pathway.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Euler's method provides an iterative approach to solve ODEs by discretizing the time domain, allowing for approximations of solutions based on initial values and derivations. However, its simplicity leads to limitations in accuracy and stability for larger problems.
Detailed
Detailed Explanation of Euler's Method
Euler's method is one of the most fundamental techniques for solving ordinary differential equations (ODEs), particularly useful when exact solutions are difficult to attain. It approximates the solution of an ODE by discretizing the time interval into small steps, known as the step size (h). The core principle of Euler's method rests on the derivative of the function involved in the ODE, leveraging it to iteratively compute solutions at successive time points.
The formula utilized in Euler's method is:
\[ y_{n+1} = y_n + h \cdot f(t_n, y_n) \]
Here, \( y_n \) represents the current approximation, \( h \) is the step size, and \( f(t_n, y_n) \) is the evaluation of the derivative at the current approximation. This leads to a new approximation for the next time step. The process begins with an initial value and continues iteratively, updating each successive value based on the previous ones.
Despite its straightforward conception, Euler's method is a first-order method, meaning that its accuracy is limited; errors accumulate and reduce linearly with smaller step sizes. This necessitates careful consideration, especially in scenarios involving stiff equations where stability issues may arise. Thus, while Euler's method is easy to implement and computationally inexpensive, users must be aware of its limitations, making it a stepping stone towards understanding more complex numerical methods like the Runge-Kutta methods.
Youtube Videos
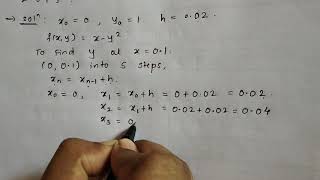
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Euler's Method
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Eulerβs method is one of the simplest and most straightforward numerical techniques for solving ODEs. It approximates the solution of the ODE by discretizing the time domain into small steps and iteratively updating the solution based on the function's derivative.
Detailed Explanation
Euler's Method is designed to solve ordinary differential equations (ODEs) by breaking down the problem into smaller steps. In this method, we start with an initial point and move step by step through time intervals (or increments) based on the derivative of the function at each point. At each step, we calculate what the next value of our function would be based on the derivative, thus creating a series of approximations that represent the function over time.
Examples & Analogies
Imagine you are walking in a straight line. If you know your starting point and the direction you are moving (this represents the derivative), you can predict where you will be after a short while (the next point). By repeating this processβre-evaluating your direction and updating your positionβyou can trace your path.
The Euler Method Formula
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Given an ODE of the form:
dydt=f(t,y),y(t0)=y0
Eulerβs method approximates the solution at each step as:
yn+1=yn+hβ
f(tn,yn)
Where:
β yny_n is the approximation of the solution at step nn,
β hh is the step size (the distance between successive points),
β f(tn,yn)f(t_n, y_n) is the derivative of yy at the point (tn,yn)(t_n, y_n).
Detailed Explanation
This formula is the heart of Euler's Method. In simple terms, we start with an initial value of y at time t0. From there, we calculate the derivative f(t_n, y_n) at that point. By multiplying this derivative by a small step size h (which dictates how far we are moving in our next approximation), we get the change in y. We then add this change to our current approximation y_n to find the next approximate value y_{n+1}. This process is repeated for each step, allowing us to build the approximate solution iteratively.
Examples & Analogies
Think of this like taking small steps on a pathβeach step covers a tiny distance determined by how steep the incline is at that point. The step size represents how far you are stepping forward, and the slope represents the change in elevation. By knowing how steep the path is, you can predict where you'll end up after each small step.
How Eulerβs Method Works
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Start with an initial condition y(t0)=y0.
- Compute the derivative f(t0,y0) using the ODE.
- Use the Euler update formula to compute y1.
- Repeat the process for each subsequent step, using the previous solution to calculate the next one.
Detailed Explanation
The implementation of Euler's Method follows a straightforward sequence: you begin by identifying your starting point (the initial condition). Next, you calculate the slope (derivative) of your function at this point. Using that slope, you apply the Euler formula to find the next value of y, moving forward in time. You continue this process for each subsequent point, always re-evaluating the slope based on the most recent value of y you have calculated.
Examples & Analogies
Imagine you're filling a bathtub with water. You start with a certain amount of water (initial condition). By measuring how fast the water is flowing in (the derivative), you can estimate how much water will be in the tub after a short time (next step). As you keep adding water and measuring the flow, you build up a picture of the total water in the tub over time.
Advantages and Disadvantages of Eulerβs Method
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Advantages:
β Very simple to implement and understand.
β Computationally inexpensive.
β Disadvantages:
β Low accuracy: Eulerβs method is only a first-order method, meaning the error decreases linearly with the step size h.
β Instability: For stiff equations or large step sizes, Eulerβs method may produce inaccurate or unstable results.
Detailed Explanation
Euler's method is extremely accessible, which is one of its main advantages; it's easy to understand and implement, making it a go-to option for learning numerical solutions. However, it has significant limitations. It is a first-order method, which means that the error in approximations decreases only linearly as the step size h gets smaller. Additionally, this method can lead to inaccuracies when dealing with stiff equations, where larger step sizes can cause drastic errors in the results.
Examples & Analogies
Consider Euler's Method like using a basic measuring tape that you can only use to measure in one-foot increments. While this is simple and straightforward (easy to understand), if you need precision (like measuring something small or fine), it can lead to large errors. Especially if the object (the scenario you're measuring) has intricate detailsβit could lead to an oversimplified and inaccurate representation.
Euler's Method Example
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For the ODE:
dydt=y,y(0)=1
Euler's method approximates the solution at each step as follows:
β Let h=0.1 be the step size.
β For t0=0,y0=1:
y1=y0+hβ
f(t0,y0)=1+0.1β
1=1.1
β Repeat for the next steps, updating yn using the Euler formula.
Detailed Explanation
In this example, we are solving the initial value problem where the rate of change of y is equal to y itself, starting at t=0 with y=1. We choose a step size of 0.1. The first calculation updates our initial condition by calculating the derivative, which is also 1 at this point. Using the Euler formula, we find the next approximate value y1 by adding the change (0.1) to our current value (1), resulting in 1.1. We would then repeat this process for further time steps to continue approximating the solution.
Examples & Analogies
This resembles keeping track of a plant's growth over time. If today (t0) the plant is 1 inch tall and grows at a constant rate of 1 inch per day, then after a day of time (with a chosen increment of 0.1 days), you estimate it will be 1.1 inches tall. By measuring a little each day, you can get a continuous approximation of the plant's height.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Euler's Method: A numerical technique for approximating solutions of ODEs using iterative calculations.
-
Step Size (h): Crucial in determining the accuracy of the method; smaller steps yield more precise results.
-
Derivative Function (f): Represents how the dependent variable changes concerning the independent variable. Essential for updates in approximations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For the differential equation dy/dt = y, y(0) = 1, applying Euler's method iteratively will yield values for 'y' that approximate the solution at increments of the step size, h.
-
Using h = 0.1, the first few values calculated would be y(0.1) = 1.1, y(0.2) = 1.21, progressively approaching the true solution of the ODE.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
To find y next, just look at y now, plus h times f, it shows you how.
π Fascinating Stories
-
Imagine you're hiking up a hill, but instead of jumping up, you take careful steps. Each step is like your 'h', and you gauge the steepness of the hill as your 'f' shows you how high to go next.
π§ Other Memory Gems
-
Remember 'h=f' to find how much you step up from where you are, making progress one step at a time.
π― Super Acronyms
H.A.S. - **H**iney **A**pproximation **S**teps (to remember how we approximate at each step).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Ordinary Differential Equation (ODE)
Definition:
An equation involving functions of a single variable and their derivatives.
-
Term: Initial Value Problem (IVP)
Definition:
A type of problem where a solution to an ODE is sought given initial conditions.
-
Term: Step Size (h)
Definition:
The increment used for advancing from one point to the next in numerical methods.
-
Term: Derivative
Definition:
The rate at which a function is changing at any given point.
-
Term: Firstorder Method
Definition:
A numerical method where the error decreases linearly with step size.
-
Term: Stiff Equation
Definition:
An ODE that exhibits rapid changes, often leading to numerical instability.