Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Numerical Methods for ODEs
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will discuss numerical methods for solving ordinary differential equations, also known as ODEs. Can someone tell me what an ODE is?
An ODE is an equation relating a function to its derivatives.
Correct! They are key in modeling real-world phenomena. Why do you think numerical methods are important for solving ODEs?
Because sometimes we can't find exact solutions, right?
Exactly! The methods we'll cover today help us find approximate solutions when analytical solutions are difficult to obtain.
Understanding Euler's Method
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs dive into our first numerical method: Eulerβs method. Itβs very straightforward! Can anyone recall the formula for this method?
Yes! It's yn+1 = yn + h β f(tn, yn).
Well done! This formula approximates the solution at each step, but it has its limitations. What do you think some of those might be?
It's low accuracy and can be unstable with stiff equations.
Precisely! Remember, while it's simple and inexpensive, itβs only first-order, meaning the accuracy can be quite limited when h is large.
Exploring Runge-Kutta Methods
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's move on to the Runge-Kutta methods, particularly RK4. Who can summarize how RK4 improves on Eulerβs method?
It uses intermediate slopes to give a better approximation!
Exactly! We calculate four slopes based on previous points to get a weighted average for the next value. Can anyone tell me what that means for the accuracy?
It results in higher accuracy, right?
Correct! However, it does come with increased computational expense. Itβs a trade-off we need to consider.
Introduction Multistep Methods
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs wrap up with multistep methods. Can someone explain what makes them different from single-step methods like Eulerβs or RK4?
They use multiple previous points to estimate the next value.
Well said! Which multistep methods did we specifically cover?
The Adams-Bashforth and Adams-Moulton methods.
Correct again! They can be more efficient and accurate, but they require information from several previous steps. Great discussion today!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Numerical methods for solving ordinary differential equations (ODEs) can vary significantly in efficiency and accuracy. This section highlights Euler's method as a simple first-order approach, Runge-Kutta methods for higher accuracy, and multistep methods which leverage previous points for better estimates. Each method's advantages and disadvantages are thoroughly examined.
Detailed
Summary of Key Concepts
In this section, we overview the key numerical methods used for solving ordinary differential equations (ODEs). Each method serves a unique purpose depending on the problem's requirements for accuracy and computational efficiency:
- Euler's Method: A basic first-order method that is very easy to implement but suffers from slow convergence and low accuracy.
- Runge-Kutta Methods: Notably the fourth-order Runge-Kutta method (RK4), which provides a better accuracy than Euler's method at the cost of higher computational demand.
- Multistep Methods: Comprising Adams-Bashforth (explicit) and Adams-Moulton (implicit) methods which utilize multiple previous solutions to improve efficiency and accuracy but require more computational resources as well.
These methods form the foundation upon which many computational techniques for solving ODEs are built, making them critical for understanding mathematical modeling across various applications.
Youtube Videos
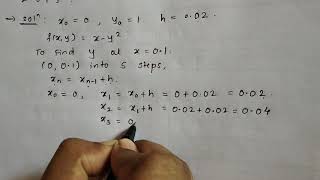
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Euler's Method Overview
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Euler's Method: A simple first-order method that is easy to implement but has slow convergence and low accuracy.
Detailed Explanation
Euler's Method is a numerical technique for solving ordinary differential equations (ODEs), particularly when analytical solutions are hard to come by. It's classified as a first-order method, meaning its accuracy is directly tied to the size of the step taken in the calculation. The method can be easily grasped and implemented, making it very accessible for those starting with numerical methods. However, this simplicity comes at a cost: the method tends to converge slowly, which means that as you try to get a more accurate answer, you might have to take very small steps, thus increasing computational effort. Its accuracy is restricted, leading to potentially significant errors, especially in scenarios where the function changes rapidly.
Examples & Analogies
Think of Euler's Method like trying to understand the shape of a twisted rope by taking photographs at regular intervals. If you take a photo every inch (big step), you might miss the intricate details (leading to low accuracy). However, if you take a photo every millimeter (small step), you can get a better idea, but it takes more time and effort (slow convergence).
Runge-Kutta Methods (RK4) Overview
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Runge-Kutta Methods (RK4): A higher-order method with faster convergence and better accuracy than Euler's method, though more computationally expensive.
Detailed Explanation
Runge-Kutta Methods, specifically the fourth-order Runge-Kutta Method (RK4), are advanced techniques used to solve ODEs more accurately than Euler's Method. RK4 achieves better precision through a calculation that involves evaluating the slope (derivative) of the function at multiple points within each step, rather than just at the beginning. This results in a 'weighted average' of these slopes and provides a significantly more accurate estimate of the function's value at the next step. Although it requires more computations (and thus is costlier in terms of processing time), the improvements in accuracy make it a preferred choice in many applications.
Examples & Analogies
Imagine you're trying to draw a curved road on a map. If you only mark points along the road one after the other (like Euler's Method), you might lose track of the gentle curves. Instead, if you take several measurements as you move along the road and average them out (like RK4), you end up with a much smoother and more accurate representation of the roadβs path.
Multistep Methods Overview
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Multistep Methods (Adams-Bashforth and Adams-Moulton): Use previous points to estimate the solution, offering better efficiency and accuracy, but requiring more computational resources.
Detailed Explanation
Multistep Methods are designed to improve efficiency and accuracy in solving ODEs by using information from multiple previous points in the approximation process. The two main types discussed are Adams-Bashforth methods, which are explicit and utilize just previous points to predict future behavior, and Adams-Moulton methods, which are implicit and combine both current and previous values for better stability and accuracy, especially useful in stiff equations. Although they provide better performance, they also demand more data and computational work because they rely on multiple evaluations to make predictions.
Examples & Analogies
Consider a chef trying to perfect a recipe. Instead of relying on just one trial (like Euler's Method), the chef uses multiple previous attempts (like Multistep Methods) to adjust the ingredients and cooking time for the best results. Though more trials can be time-consuming, the outcome is usually a much tastier dish, just as these methods yield a more accurate solution.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Euler's Method: A straightforward numerical approximation for ODEs, easy to implement but not very accurate.
-
Runge-Kutta Methods: These provide more accuracy than Euler's through additional calculations.
-
Multistep Methods: Use multiple past points to enhance the efficiency and accuracy in solving ODEs.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Applying Euler's method to dy/dt = y with y(0) = 1 and h = 0.1 gives y(0.1) approximately 1.1.
-
Using RK4 on the same differential equation updates the solution with enhanced accuracy compared to Euler's method.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Euler's simple step, don't quite prep, accuracy is low, but gives us a flow.
π Fascinating Stories
-
Imagine a mountain climber (RK4) taking careful steps at each point, asking guides (intermediate slopes) to ensure he doesnβt fall, while a casual walker (Euler) just walks straight ahead, often losing the correct path.
π§ Other Memory Gems
-
For Runge-Kutta, think: K1, K2, K3 for accuracy, add them up for a stronger guarantee.
π― Super Acronyms
RK4
- R: stands for Repeat
- K: for Knitting together slopes
- and 4 represents the four slopes!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Ordinary Differential Equation (ODE)
Definition:
An equation involving functions of a single variable and their derivatives.
-
Term: Euler's Method
Definition:
A numerical technique for approximating solutions of ODEs using a first-order difference.
-
Term: RungeKutta Methods
Definition:
Numerical methods that provide higher accuracy for solving ODEs through multiple intermediate calculations.
-
Term: Multistep Methods
Definition:
Numerical methods that use several previous solution points to define the next solution point in ODEs.