Transformation and Coordinate Frames
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Homogeneous Transformation Matrix
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to explore the homogeneous transformation matrix, or HTM. Can anyone tell me why we might need to combine rotation and translation in robotics?

So we can easily manage how a robot moves in space?

Exactly! The HTM allows us to represent a robot's position and orientation in a single format. This matrix is a 4x4 structure that encompasses both rotation, represented by a rotation matrix \( R \), and translation, represented by a displacement vector \( d \).

What does the 4x4 matrix look like?

"Good question! It's structured like this:
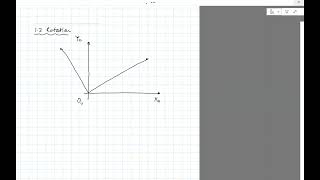
Rotation Matrices
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's dive into rotation matrices. Who can explain what a rotation matrix does?

It defines how something is rotated in space, right?

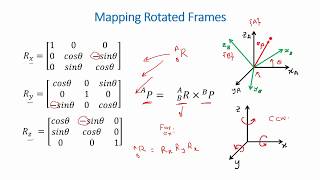
That's correct! In 3D, we can represent rotations about the axes using the following matrices: \( R_x(\theta) \), \( R_y(\theta) \), and \( R_z(\theta) \).

Are there specific rules these matrices have to follow?

Yes! They must satisfy orthogonality and have a determinant of 1 to maintain the integrity of the rotation. Always keep these properties in mind when you implement these matrices.

So, they ensure the object remains unchanged in size while just rotating?

Exactly! That's why understanding these matrices is fundamental to kinetic modeling in robotics.
Denavit-Hartenberg Parameters
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's talk about the Denavit-Hartenberg parameters. Can someone explain why we might use them?

Are they for organizing the movements of robot joints?

Yes! They provide a standard way to assign coordinate frames to the links of a manipulator. The four parameters we use are joint angle \( \theta \), link offset \( d \), link length \( a \), and link twist \( \alpha \).

How does that help us?

By reducing the complexity of kinematic equations, we can create models that are easier to understand and simulate. It streamlines our design process significantly.

Is there a practical example of using these parameters?

Definitely! They are essential in creating precise robotic arms for various tasks, ensuring that the robot can achieve the required configurations smoothly.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In the world of robotics, understanding transformations and coordinate frames is crucial. This section explains the homogeneous transformation matrix, rotation matrices, and Denavit-Hartenberg parameters, which together simplify the modeling of robotic systems and their movements in 3D space.
Detailed
Detailed Summary
In this section, we delve into the essential mathematical frameworks that enable robots to interpret and execute complex movements. Key points include:
1. Homogeneous Transformation Matrix
The homogeneous transformation matrix combines rotation and translation into a single 4×4 matrix, allowing for seamless manipulation of robotic movements. The matrix format is:
[R d] T = [0 1]
where \( R \) is the rotation matrix and \( d \) is the displacement vector. This matrix is fundamental in converting between different coordinate frames, which is essential in planning and executing robot trajectories.
2. Rotation Matrices
Rotation matrices define the orientation of a frame in 3D space. The common forms for 3D rotations around the x, y, and z axes are represented as:
- \( R_x(\theta) \)
- \( R_y(\theta) \)
- \( R_z(\theta) \)
These matrices must meet orthogonality conditions (i.e., the inverse is equal to the transpose) and have a determinant of 1 to ensure proper rotational characteristics.
3. Denavit-Hartenberg (DH) Parameters
The DH parameters provide a standardized method for assigning coordinate frames to links of a robotic manipulator. The parameters include:
- \( \theta \): joint angle
- \( d \): link offset
- \( a \): link length
- \( \alpha \): link twist
These parameters allow for the simplification of kinematic equations, making model building more systematic and organized. Understanding their application is key for designing effective robotic systems.
Youtube Videos







Audio Book
Dive deep into the subject with an immersive audiobook experience.
Homogeneous Transformation Matrix
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Homogeneous Transformation Matrix
- Combines rotation and translation into a single 4×4 matrix.
- General form:
\[ T = \begin{bmatrix} R & d \ 0 & 1 \end{bmatrix} \]
where R is rotation matrix, d is displacement vector.
Detailed Explanation
A Homogeneous Transformation Matrix is used in robotics to represent both the position and orientation of a robotic element in space. It combines two essential components: rotation and translation. The matrix is a 4x4 array where the upper left 3x3 section represents the rotation (how the robot is oriented), and the last column represents the translation (where the robot is located in space). The last row, [0 0 0 1], is a standard way to incorporate these transformations into mathematical calculations.
Examples & Analogies
Imagine you are using a remote-controlled car. If you want the car to move forward and turn at the same time, you need a way to combine the direction it should face (rotation) and how far it should go (translation). The Homogeneous Transformation Matrix is like a set of instructions that tells the car how to move in 3D space all at once.
Rotation Matrices
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Rotation Matrices
- Used to define orientation of a frame in space.
- 3D rotations represented using matrices like:
- \( R_x(θ) \)
- \( R_y(θ) \)
- \( R_z(θ) \)
- Must satisfy orthogonality and determinant = 1.
Detailed Explanation
Rotation matrices are mathematical tools that represent how a frame or coordinate system is oriented in 3D space. There are different rotation matrices for each axis (X, Y, Z), and they ensure that when transformed, the object retains its geometric properties. Orthogonality means that the axes remain perpendicular after rotation, and having a determinant of 1 ensures that the area and volume are preserved during transformations.
Examples & Analogies
Think of rotating a cube in front of you. If you turn it around, the orientation changes, but the cube's shape doesn’t distort. Rotation matrices are like the detailed steps you might write down: 'Turn left by 30 degrees', and they ensure that you achieve the perfect rotation without losing the cube's dimensions.
Denavit–Hartenberg (DH) Parameters
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Denavit–Hartenberg (DH) Parameters
- Standard method for assigning coordinate frames to links.
- Parameters:
- θ (theta) – joint angle
- d – link offset
- a – link length
- α (alpha) – link twist
- Helps reduce kinematic equations and systematize model building.
Detailed Explanation
Denavit-Hartenberg (DH) Parameters are a systematic way to define the geometry of robot arms. Each link and joint of the robot is assigned parameters that describe its position and relationship to the next link. This standardized method simplifies the complex calculations involved in robotic movements, allowing for easier programming and simulation of robotic systems.
Examples & Analogies
Imagine assembling a set of building blocks according to specific guidelines. Each block's size and position are akin to the DH parameters. By following these guidelines (like ‘this block should be 2 cm long’ or ‘rotate this by 90 degrees’), you can build a stable structure (or robot) that behaves predictably as it moves.
Key Concepts
-
Homogeneous Transformation Matrix: Utilized to combine rotation and translation during robotic motion.
-
Rotation Matrix: Defines how a robot's components are rotated in 3D space.
-
Denavit-Hartenberg Parameters: Framework for systematically assigning coordinate frames to robot joints to simplify kinematics.
Examples & Applications
Example of Homogeneous Transformation: A robot arm uses an HTM to transition from one end of a workspace to another by clearly defining its position and orientation.
Example of Rotation Matrices: A robot rotating its end effector around the z-axis to position a tool correctly for a specific task.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In motion with grace, remember the place, HTM takes you fluent, without a trace.
Stories
Imagine a robot seeking a treasure; it needs to know how to turn and where to go. The transformation matrix is its map, the rotations help it avoid traps, and DH parameters guide the way through the maze.
Memory Tools
For DH parameters, remember 'TALD' - Theta, A, Link Length, and Distance.
Acronyms
Use 'HRT' for Homogeneous Rotation Transformation to recall the combination of rotation and translation.
Flash Cards
Glossary
- Homogeneous Transformation Matrix
A 4×4 matrix that combines rotation and translation, facilitating the representation of position and orientation in 3D space.
- Rotation Matrix
A matrix used to perform rotations in 3D space, maintaining the object's size and shape during the transformation.
- DenavitHartenberg Parameters
Standard parameters used to assign coordinate frames to robotic links, simplifying the kinematic equations for robotic systems.
Reference links
Supplementary resources to enhance your learning experience.
