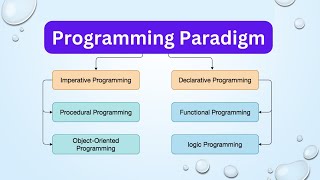
Functional Programming Paradigm
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Functional Programming
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today we're going to explore functional programming. Can anyone tell me what they think functional programming is?

Is it just programming with functions? Like, I mean, we write functions in other paradigms too, right?

Great question! Functional programming indeed uses functions, but it treats computation as the evaluation of mathematical functions. This means we aim to avoid changing state or using mutable data.

What does immutability mean in this context?

Good inquiry! Immutability means that once a data structure is created, it cannot be changed. This helps prevent side effects, which will make it easier to reason about our code.

So, by avoiding side effects, we can reduce bugs, right?

Exactly! That's one of the significant advantages of functional programming.

In summary, functional programming emphasizes pure functions, immutability, and avoids changing state. These features lead to easier-to-understand and less error-prone code.
Core Concepts of Functional Programming
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's talk about pure functions. Can anyone tell me why they're called 'pure'?

I think it's because they don't depend on outside states?

Exactly! Pure functions always produce the same output given the same input. Now, what about first-class functions?

Are those functions that can be assigned to variables or passed as arguments?

Right! In functional programming, functions are first-class citizens, which means they can be treated like any other data type. This leads to what's called higher-order functions.

Can you give me an example of a higher-order function?

Sure! A higher-order function can take a function as an argument or return a function. For example, the 'map' function takes a function and applies it to each element in a list.

To sum up, we discussed pure functions, first-class functions, and higher-order functions. These concepts are vital to understanding the power of functional programming.
Recursion and Lazy Evaluation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s dive into recursion! Can anyone explain how recursion works in programming?

I think it's when a function calls itself until it hits a base case?

Exactly! Recursion is often used instead of loops in functional programming. Now, what about lazy evaluation?

Isn’t that about delaying the execution of expressions until their results are needed?

Yes! Lazy evaluation can improve performance because it avoids unnecessary computation.

How do these concepts help with concurrent programming?

Both recursion and lazy evaluation enable better handling of state and side effects, making it easier to write concurrent code that is reliable. In summary, recursion and lazy evaluation are essential features of functional programming that help manage complex computations.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Functional programming is a paradigm that focuses on pure functions, immutability, and higher-order functions, enabling less error-prone code by avoiding side effects. It is particularly useful for concurrent computing and managing state changes.
Detailed
Functional Programming Paradigm
Functional programming (FP) is a programming paradigm that treats computation as the evaluation of mathematical functions and avoids changing state or mutable data. It emphasizes the use of pure functions, which are functions that always produce the same output for the same input and have no side effects. This approach leads to more predictable and understandable code. Key concepts in functional programming include immutability (the idea that data cannot be changed after it is created), first-class functions (functions treated as first-class citizens), higher-order functions (functions that can take other functions as arguments), recursion (using functions that call themselves), and lazy evaluation (delaying computation until its result is needed).
Key Points:
- Pure Functions: Functions that do not cause any side effects.
- Immutability: Data that cannot be modified after it is created.
- First-Class and Higher-Order Functions: Functions treated as data, allowing them to be passed as arguments or returned from other functions.
- Recursion: A method for defining functions in terms of themselves, often used in place of traditional looping.
- Lazy Evaluation: Only evaluating expressions when necessary, which can improve performance.
Significance:
Understanding FP is crucial for working with languages like Haskell, Lisp, and Scala, which heavily emphasize this paradigm. It provides developers with tools to write cleaner, more maintainable, and scalable software, especially in concurrent or parallel systems.
Youtube Videos

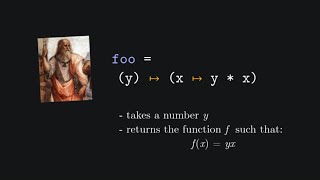






Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Functional Programming
Chapter 1 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Functional programming (FP) treats computation as the evaluation of mathematical functions and avoids changing state or mutable data.
Detailed Explanation
At its core, functional programming is concerned with the idea that any computation can be modeled as the evaluation of functions. Unlike other programming styles, FP avoids changing the state of its data, which means it prefers to work with data that does not change (immutable data). This aligns well with mathematical concepts, where functions take inputs and produce outputs without side effects. Think of it like a mathematical equation where you have a fixed input, and you can always expect the same output from it.
Examples & Analogies
Imagine a vending machine that operates as a function. When you input a specific amount of money and select a button, you always get the same item in return. The internal state of the machine doesn’t change unless it’s replenished. Just like in functional programming, the outcome is predictable and consistent.
Key Features of Functional Programming
Chapter 2 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Pure functions
• Immutability
• First-class and higher-order functions
• Recursion instead of loops
• Lazy evaluation
Detailed Explanation
Functional programming comes with several key features that define it:
1. Pure Functions: These functions always produce the same output for the same input and do not have side effects. For instance, a function that adds two numbers will always return the same result without modifying any external state.
- Immutability: Data is immutable, meaning once it's created, it cannot be changed. Instead of altering existing data, new data is derived from it. This helps in preventing bugs related to unexpected changes.
- First-class and Higher-order Functions: Functions are treated as first-class citizens, meaning they can be passed as arguments, returned from other functions, and assigned to variables. Higher-order functions are functions that take other functions as parameters or return them.
- Recursion Instead of Loops: FP often relies on recursion to perform repetitive tasks rather than traditional loops. This means a function calls itself to solve smaller instances of the same problem.
- Lazy Evaluation: This is a strategy where evaluations of expressions are deferred until their results are needed. It's a way of optimizing performance by preventing unnecessary calculations.
Examples & Analogies
Imagine a chef in a kitchen. A pure function is like a recipe that always outputs the same dish (like a cake) for a specific combination of ingredients without any surprises. Immutability can be compared to preparing a dish without ever putting the original ingredients back into the raw state; once you mix flour, sugar, and eggs, you cannot revert them. Higher-order functions resemble a dish where you can add various toppings based on your personal preference, while recursion is akin to a chef repeatedly chopping ingredients until they are diced just right without using a machine. Lastly, lazy evaluation is like letting the chef prepare additional sides only if the diners request them, rather than making everything upfront.
Languages that Support Functional Programming
Chapter 3 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Haskell
• Lisp
• Scala
• Elixir
• JavaScript (partially)
Detailed Explanation
Several programming languages are tailored for functional programming, offering built-in features that support its principles:
- Haskell: A purely functional programming language known for its strong type system and lazy evaluation.
- Lisp: One of the earliest programming languages, known for its deep capabilities in functional programming with support for first-class functions.
- Scala: A language that combines object-oriented and functional programming, providing flexibility for developers.
- Elixir: Built on the Erlang VM, it embraces functional programming and is known for its scalability.
- JavaScript (partially): While primarily an object-oriented language, JavaScript supports functional programming constructs, allowing developers to use functions as first-class citizens.
Examples & Analogies
Consider different chefs specializing in various cuisines. Each cuisine represents a programming language. Haskell could be likened to a chef who strictly adheres to traditional French techniques, ensuring every dish is elevated to perfection with no room for error (pure functions). Lisp might be compared to an inventor chef who's not afraid to experiment. Scala represents a fusion chef who brings together the best of both worlds, while Elixir symbolizes a chef adept at handling large orders efficiently. JavaScript would be analogous to a versatile chef who can switch between different styles based on the requirements of the patrons, still having foundational elements of classical techniques.
Example of Functional Programming
Chapter 4 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Example (Haskell)
square x = x * x
main = print (square 5)
Detailed Explanation
This Haskell example defines a simple function, square, that takes a number x and returns its square (x times x). Here’s what happens step by step:
- The function square is defined with the syntax square x = x * x, where x is the input parameter.
- In the main function, the print statement is called to display the result of square 5. When 5 is passed to square, it calculates 5 * 5 and outputs 25. This is a straightforward representation of a pure function with predictable output based on its input.
Examples & Analogies
Imagine you have a magical calculator that, whenever you input a number, it gives you back the result of that number squared. If you say '5', it will without fail compute and return '25'. The function is consistent and reliable, much like how in functional programming the output remains the same for the same input, with no hidden changes or effects.
Advantages of Functional Programming
Chapter 5 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Easier to reason about
• Fewer bugs due to immutability
• Suitable for concurrent and parallel computing
Detailed Explanation
Functional programming offers several advantages:
1. Easier to Reason About: Since functions are independent and do not alter any external state, it's easier to foresee how a program will behave, making debugging and testing simpler.
2. Fewer Bugs Due to Immutability: By using immutable data structures, FP reduces the chances of bug incidence, particularly those related to unexpected data changes, which can cause difficult-to-trace issues.
3. Suitable for Concurrent and Parallel Computing: Because functional programs avoid shared state, they can easily run in parallel, making them excellent for multi-threaded and distributed systems.
Examples & Analogies
Consider a librarian who only allows books to be read without ever marking or changing them. This system reduces mistakes by ensuring that no one accidentally misplaces or alters a book (immutability). Similarly, if multiple readers (tasks) can read books at once without disturbing one another, it's like how functional programming optimizes for concurrency, allowing multiple computations to occur without interference.
Limitations of Functional Programming
Chapter 6 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Performance overhead due to recursion
• Not intuitive for beginners
• Limited libraries for certain tasks
Detailed Explanation
Despite its strengths, functional programming has some limitations:
1. Performance Overhead Due to Recursion: Recursive functions can lead to performance issues as they can consume more memory and stack space than traditional iterative loops, especially for deep recursion.
2. Not Intuitive for Beginners: The concepts of functional programming may be difficult for those accustomed to imperative programming styles. Beginners may find the lack of step-by-step instructions and mutable states confusing.
3. Limited Libraries for Certain Tasks: Compared to widely used imperative languages, functional programming may have fewer libraries or frameworks available for specific, practical tasks.
Examples & Analogies
Think of a person who insists on doing everything by following recipes precisely (functional programming), as opposed to following their instincts or improvising in the kitchen (imperative programming). If the recipe calls for a complex technique, it might take longer to prepare a meal, while someone who intuitively adjusts based on experience might whip something up faster. This also highlights the struggle beginners might face when learning such a rigid style compared to the creative freedom of another approach.
Key Concepts
-
Functional Programming: A paradigm that avoids mutable data and emphasizes pure functions.
-
Pure Functions: Functions that prevent side effects and provide predictable outputs.
-
Immutability: A crucial feature that enables safer and more reliable code.
-
First-Class Functions: Treating functions as first-class citizens allows passing them as arguments.
-
Higher-Order Functions: Functions that can accept or return other functions.
-
Recursion: A powerful feature to repeat function calls in place of traditional loops.
-
Lazy Evaluation: An optimization that evaluates expressions only when necessary.
Examples & Applications
An example of a pure function in Haskell is square x = x * x, which consistently returns the square of a number without altering any external state.
The use of the map function in JavaScript, which accepts a function and applies it to each element in an array, serves as a classic illustration of higher-order functions.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Functional programming's quite the hit, with pure functions that never quit; never side effects, always the same, modules so clean, they play the game.
Stories
Imagine a library where every book contains a story that never changes, and each reader can create a new path to the climax by choosing different narratives—this is how pure functions operate, leading to consistency without change.
Memory Tools
Remember 'PILHS' for Functional Programming: P for Pure Functions, I for Immutability, L for Lazy Evaluation, H for Higher-Order Functions, S for State Avoidance.
Acronyms
Use the acronym 'HILA' to remember key concepts in Functional Programming
for Higher-Order Functions
for Immutability
for Lazy Evaluation
for Avoiding side effects.
Flash Cards
Glossary
- Functional Programming
A programming paradigm focused on the use of pure functions and avoiding mutable data.
- Pure Functions
Functions that always return the same output for the same input and do not have side effects.
- Immutability
The property of an object or data structure that prevents it from being changed after it is created.
- HigherOrder Functions
Functions that can take other functions as arguments or return them as results.
- Recursion
A method where a function calls itself to solve smaller instances of the same problem.
- Lazy Evaluation
A strategy of delaying the evaluation of an expression until its value is needed.
Reference links
Supplementary resources to enhance your learning experience.
