Conclusion and Transition
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Recap of Key Concepts
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Welcome everyone! Before we dive into self-biased amplifiers, let's recap our previous discussions. Can anyone remind me about the characteristics of the common emitter amplifier with fixed bias?

It has a voltage gain and its frequency response includes low pass and high pass characteristics.

Excellent! Remember, the frequency response is crucial for understanding how amplifiers work across different ranges. What about our analysis of the R-C and C-R circuits?

The R-C circuit responds at low frequencies while the C-R responds better at high frequencies.

Very good! So, when we combined these amplifiers, what kind of frequency response did we observe?

We got a combined frequency response, resulting in a cutoff frequency!

Right! Always keep in mind, this combination helps mitigate adverse effects on overall performance. Now, let’s look forward to self-biased amplifiers.
Introduction to Self-Biased Amplifiers
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's transition to self-biased amplifiers. Can anyone explain why self-biasing might be useful in practical applications?

It provides better stability and requires fewer external components, which simplifies the design.

Exactly! Self-biasing maintains stable performance with varying temperature and transistor parameters. What do you expect from the design guidelines we will cover next?

I think we might learn how to select values of coupling capacitors based on cutoff frequencies.

That's correct! Selecting values optimally will enhance overall circuit performance. Always consider how frequency response ties into these choices.
Numerical Example Usage
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

As we move forward, let’s reflect on why numerical examples are so important in our discussions. Anyone want to share their thoughts?

Numerical examples help us apply theoretical concepts to real-world scenarios!

Absolutely! They allow us to explore various configurations and tuning aspects, including how values interact in our circuits. What is the consequence of a poorly selected coupling capacitor?

It could lead to inadequate frequency response, affecting the amplifier’s performance drastically.

Well answered! The takeaway here is that numerical examples not only illustrate concepts but also hone our design skills. Let's apply this understanding to the self-biased amplifier in the next session.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The conclusion effectively transitions students from understanding common emitter amplifiers with fixed bias to self-biased amplifiers. This section provides a recap of key concepts covered previously and outlines the practical implications of numerical examples, particularly in the design of circuits for specific cutoff frequencies.
Detailed
In this section, Professor Pradip Mandal summarizes the previous discussions on the frequency response of common emitter (CE) amplifiers with fixed bias and introduces the subject of self-biased CE amplifiers. He emphasizes the importance of understanding the numerical aspects and design choices in selecting capacitive components for amplifiers. The overall plan is to build on prior knowledge by recapping essential parts of the R-C and C-R circuit analysis, focusing on transitioning students to the practical implications of the design throughput numerical examples that will help inform decisions on coupling and load capacitance. This section suggests a systematic approach to link theoretical concepts with their practical applications, which is vital for students aiming to implement these principles in real-world electronics.
Youtube Videos

Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Discussed Topics
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, in the previous week we have discussed about the frequency response of CE amplifier for which we have detail discussion about R-C and C-R circuit and then you know we have discussed about the common source amplifier particularly with circuit analysis.
Detailed Explanation
In this section, the speaker summarizes the topics covered in the previous week. They particularly highlight the frequency response analysis of the Common Emitter (CE) amplifier, including the use of R-C and C-R circuits, and also the analysis of the Common Source (CS) amplifier. Understanding these concepts is crucial as they are foundational for analyzing amplifier circuits.
Examples & Analogies
Think of this like reviewing chapters in a book before starting a new one. You want to ensure you've understood the previous material as it lays the groundwork for what's coming next. In electronics, mastering frequency response helps predict how circuits will behave in different scenarios, just as understanding plot points helps in following a story.
Focus on Self-Biased CE Amplifier
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
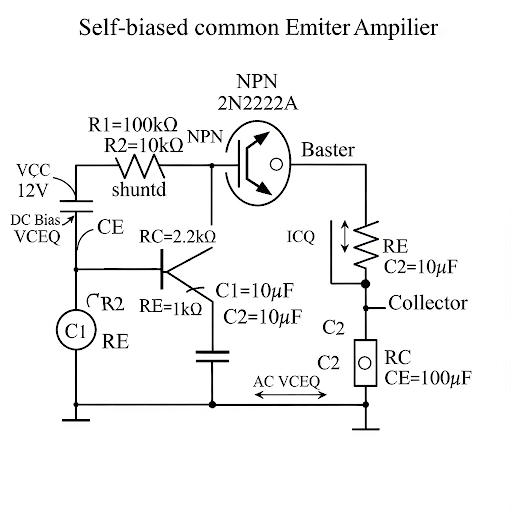
So, we are going to start with the common emitter amplifier with self-biased and its corresponding circuit analysis.
Detailed Explanation
Here, the speaker introduces the main focus of the current session: analyzing a self-biased Common Emitter amplifier. This type of amplifier is essential in practical applications because it provides stable biasing, which is crucial for consistent performance in amplifying signals.
Examples & Analogies
Imagine a self-biased amplifier like a thermostat in your home. Just like a thermostat keeps the temperature stable without manual adjustments, a self-biased amplifier maintains its operating point despite variations in temperature or transistor characteristics, ensuring reliable performance.
Recap of R-C and C-R Circuit Analysis
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
We need to just recapitulate some part of it, particularly the R-C circuit and C-R circuit analysis which it has been deployed for fixed bias circuit and then we will be moving to the common emitter amplifier with self-bias.
Detailed Explanation
This chunk emphasizes the importance of revisiting the analysis of R-C and C-R circuits. These concepts were applied to the fixed bias circuit, and understanding them is necessary before tackling the self-bias configuration. Revisiting these fundamentals helps solidify the foundation needed for more advanced analysis.
Examples & Analogies
Think of it as revising vocabulary before writing a language essay. Just as you wouldn't want to struggle with words while expressing ideas, it's equally important to be comfortable with circuit analysis basics before diving into more complex amplifier designs.
Numerical Examples for Application
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
From these numerical examples, we will get an idea that how to select the value of different capacitive components in the circuit.
Detailed Explanation
The speaker points out that numerical examples will be provided to illustrate how to choose specific component values, particularly capacitors, in the design of an amplifier circuit. Understanding these selections is vital for tailoring the amplifier's frequency response to meet specific performance criteria.
Examples & Analogies
Selecting component values is somewhat like adjusting ingredients in a recipe. Just like you adjust flour and sugar to achieve the right taste in baking, choosing the correct capacitor values ensures that the amplifier will perform optimally for the desired frequency range.
Conclusion and Transition to New Topics
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, we will be discussing about some numerical examples. But before that we are going to discuss about the frequency response of common emitter amplifier with self-bias arrangement.
Detailed Explanation
The final chunk prepares students for the transition into new material, following the examination of numerical examples. This sets the stage for discussing the frequency response of the self-biased CE amplifier, indicating a shift in focus towards practical applications and evaluations of the concepts learned.
Examples & Analogies
Consider this transition like moving from the theory of cooking to actually preparing a meal. Just as you learn techniques before cooking a dish, students first study numerical examples before applying this knowledge to analyze real-world amplifier behavior. This ensures they have both the theoretical understanding and practical skills.
Key Concepts
-
Self-Biasing: A method that utilizes feedback to keep biasing stable in amplifiers.
-
Numerical Examples: Practical scenarios used to reinforce theoretical concepts for better understanding.
Examples & Applications
Designing a self-biased amplifier with specific cutoff frequencies using chosen capacitor values.
Adjusting the coupling capacitor in a circuit to visualize its effect on frequency response.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When amplifiers strive and circuits do play, self-biasing's the game to keep failures at bay.
Stories
Imagine an amplifier that kept changing its output; it decided to listen to its own feedback to keep stabilized, which resulted in steady performance despite the noise around it.
Memory Tools
Remember 'CUT OFF = Change Under Transmission Of Frequencies' for cutoff frequency.
Acronyms
Self-Bias (S-B)
Stability
Balance
and Feedback.
Flash Cards
Glossary
- SelfBiased Amplifier
An amplifier configuration that maintains stable biasing through feedback from its own output.
- Frequency Response
The measure of an amplifier's output spectrum in response to an input signal, expressed in terms of frequency.
- Cutoff Frequency
The frequency at which the output of a circuit begins to decline, marking the boundary between pass and stop bands.
Reference links
Supplementary resources to enhance your learning experience.
