Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Pressure in Fluids
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we are going to explore how pressure in a fluid changes with depth. Can anyone tell me what they think happens to pressure as you go deeper in water?
I think it gets higher because there is more water above you.
Exactly! The weight of the water above adds to the pressure. Can anyone recall the formula we use to express that relationship?
Is it P = Pa + Οgh?
That's correct! 'P' is the pressure at depth, 'Pa' is atmospheric pressure, 'Ο' is the density of the fluid, 'g' is the acceleration due to gravity, and 'h' is the depth. Let's remember the acronym 'PAGH' for pressure, atmospheric pressure, gravity, and height. What does this tell us about the pressure at different depths?
It shows that pressure increases linearly with depth!
Exactly! That's a key concept. Pressure increases uniformly with each unit of depth in a fluid.
Relation of Density to Pressure
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, letβs talk about density. Does anyone know how the density of a fluid affects the pressure at a given depth?
I think denser fluids will create more pressure at the same depth.
Very good! If the fluid's density increases, the pressure at a certain depth also increases. This is why different fluids, like oil and water, exert different pressures at the same depth. If we take a container of water and another of oil, which one do you think would have greater pressure at the same depth?
The oil, if it's denser!
Right! Remember that density plays a critical role in this variation. So always consider the fluid type when thinking about pressure.
Gauge Pressure
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's discuss gauge pressure. Who can explain what gauge pressure is?
Isn't it the pressure difference between the pressure at a certain depth and the atmospheric pressure?
Correct! Gauge pressure is calculated as P - Pa. Why do we often use gauge pressure in practical applications?
Because atmospheric pressure can vary and we usually want a reading relative to it.
Exactly! Instruments like tire pressure gauges give you gauge pressure as it's more practical for everyday use.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section discusses the variation of pressure with depth in a fluid at rest, establishing the relationship between pressure, fluid density, and gravitational acceleration. It introduces mathematical formulations and practical applications like gauge pressure.
Detailed
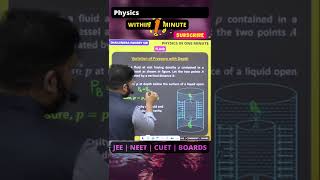
In a fluid at rest, pressure increases with depth due to the weight of the overlying fluid. The pressure difference between two points in a fluid, P2 and P1, separated by a vertical distance h, can be expressed as P2 - P1 = Οgh, where Ο is the fluid's density and g is the acceleration due to gravity. When the top point (P1) is at the surface of a liquid open to atmospheric pressure, the absolute pressure at any depth h is given by P = Pa + Οgh. This section emphasizes that the shape or area of the container does not affect the pressure at a given depth, highlighting that pressure in a liquid is the same at any horizontal level in an incompressible fluid, leading to applications such as gauge pressure calculations.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Pressure at Different Depths
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Consider a fluid at rest in a container. In Fig. 9.3 point 1 is at height h above a point 2. The pressures at points 1 and 2 are P1 and P2 respectively. Consider a cylindrical element of fluid having area of base A and height h. As the fluid is at rest the resultant horizontal forces should be zero and the resultant vertical forces should balance the weight of the element. The forces acting in the vertical direction are due to the fluid pressure at the top (P1A) acting downward, at the bottom (P2A) acting upward. If mg is weight of the fluid in the cylinder we have (P2 β P1) A = mg.
Detailed Explanation
In a fluid that is at rest, pressure varies with depth due to the weight of the fluid above. When you consider two points at different heights within the fluid, point 1 is higher than point 2. The pressure at point 2 (deeper) is influenced by both the pressure at point 1 and the weight of the fluid column that is above point 2. The balance of forces ensures that the upward pressure force from point 2 equals the weight of the fluid column (the force acting downward). This establishes the relationship that pressure increases with depth.
Examples & Analogies
Think about when you dive underwater; the deeper you go, the more pressure you feel against your body due to the weight of the water above you. This is why scuba divers must be trained about how to manage pressures at various depths.
Pressure Difference and Density Relation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, if Ο is the mass density of the fluid, we have the mass of fluid to be m = ΟV= ΟhA so that P2 β P1= Οgh.
Detailed Explanation
Using the relationship derived from balancing the forces, we can express the pressure difference (P2 β P1) between the two points in terms of density (Ο) of the fluid and the height difference (h) between the two points. This leads us to the formula P2 - P1 = Οgh, showing that the pressure difference increases with both the density of the fluid and the height difference.
Examples & Analogies
Imagine a heavy pile of books stacked on your chest. The weight of those books pressing downβrepresenting the density of the fluidβcreates a feeling of pressure. If you were to stack even more books (increasing the height), the pressure (or weight you feel) increases too, similar to how fluid pressure builds up as you go deeper underwater.
Gauge Pressure Explained
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Thus, the pressure P, at depth below the surface of a liquid open to the atmosphere is greater than atmospheric pressure by an amount Οgh. The excess of pressure, P β Pa, at depth h is called a gauge pressure at that point.
Detailed Explanation
When you measure the pressure underwater, you are measuring the total pressure, which includes both the atmospheric pressure at the surface (Pa) and the additional pressure due to the water column above (Οgh). The pressure that exceeds atmospheric pressure is referred to as gauge pressure, which is important in various applications, like scuba diving or engineering.
Examples & Analogies
Think of how a pressure gauge on a tire works: it shows the pressure inside the tire (gauge pressure) which must be above the atmospheric pressure to keep the tire inflated. In a similar way, when submerged, the gauge pressure provides important information about the forces acting due to the fluid in addition to the normal atmospheric pressure.
Hydrostatic Paradox
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The area of the cylinder is not appearing in the expression of absolute pressure in Eq. (9.7). Thus, the height of the fluid column is important and not cross-sectional or base area or the shape of the container. The liquid pressure is the same at all points at the same horizontal level (same depth).
Detailed Explanation
This principle reveals the 'hydrostatic paradox' where the pressure due to a liquid depends solely on the height of the liquid column, regardless of the shape or size of the container holding it. Therefore, if two containers are filled to the same height with the same liquid, the pressure at any horizontal level will be the same, thereby illustrating that pressure is dependent on depth, not the volume or shape of the fluid.
Examples & Analogies
If you fill three different vesselsβone tall and skinny, one short and wide, and one odd-shaped but filled to the same height with waterβeach will exert the same pressure at the same depth, even though they hold different amounts of water. This is surprising and underscores the principle that pressure in fluids doesnβt care about the shape of the container, just the height.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Pressure increases with depth due to the weight of the liquid above.
-
Gauge pressure measures pressure above atmospheric pressure.
-
Pressure in a liquid is uniform at the same horizontal level.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If a diver is 10 meters underwater, the pressure exerted on them will be greater than at the surface by an amount equal to Οgh, where Ο is the density of water, g is gravity, and h is 10m.
-
A barometer measures atmospheric pressure, which can be expressed as the height of mercury in a column.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
At depth we go, pressure will grow!
π Fascinating Stories
-
A fish swimming deeper in the ocean feels the weight of the water above, pressing down harder and harder as it dives deeper.
π§ Other Memory Gems
-
Remember 'PAGH' - Pressure, Atmospheric pressure, Gravity, and Height for the pressure equation!
π― Super Acronyms
DAG
- Density Affects Gauge pressure.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Pressure
Definition:
The force exerted per unit area on a surface.
-
Term: Gauge Pressure
Definition:
The pressure measured relative to atmospheric pressure.
-
Term: Absolute Pressure
Definition:
The total pressure exerted including atmospheric pressure.
-
Term: Density (Ο)
Definition:
The mass per unit volume of a substance.
-
Term: Incompressible Fluid
Definition:
A fluid with a constant density, regardless of the pressure applied.
-
Term: Hydrostatic Pressure
Definition:
The pressure exerted by a fluid at rest due to the weight of the fluid above it.