Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Marginal Product
Unlock Audio Lesson
Let's start our discussion with the concept of *marginal product*. Who can tell me what this term means?
I believe marginal product refers to the extra output produced by adding one more unit of input.
Exactly! It represents the additional output that results when one more unit of a variable input, like labor, is added. Can anyone provide the formula for this concept?
It's MP = \(\Delta TP / \Delta L\), right?
Perfect! Remember that \(\Delta TP\) is the change in total product and \(\Delta L\) is the change in the input. Now why is this concept important in production?
It helps firms determine the best input combinations to maximize their output and profit.
Great observation! Understanding MP is key for making efficient production decisions.
The Law of Diminishing Marginal Returns
Unlock Audio Lesson
Now, let’s move on to what happens to marginal product as we keep adding more of a variable input—this leads us to the law of diminishing returns. Can someone explain what that means?
It means that as we add more of a variable input while keeping others constant, the additional output we get from those inputs starts to decrease after a certain point.
Exactly! Initially, adding more labor might increase productivity significantly, but eventually, each additional worker will contribute less to output. This is due to limited resources, like land, becoming crowded.
So, if I visualize this with a production function graph, MP would rise initially, hit a peak, and then start to decline?
Correct! Creating graphs of the relationship between input and output helps illustrate this phenomenon. It's vital for understanding production efficiency.
Calculating Marginal Product
Unlock Audio Lesson
Next up, let’s practice calculating marginal product using some data. What do you think we need?
We need the total product values for different input levels, right?
Exactly! For example, if our total product increases from 10 to 24 when we add another unit of labor, how do we find the marginal product?
We subtract: 24 - 10 = 14. So, the marginal product of adding that unit is 14.
Well done! Always remember that the marginal product is the change in total product divided by the change in labor. Now, what if we add five units, what would we do?
We'd keep calculating the changes in output as we add those units, right?
Exactly, and that’s how businesses assess their productivity.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Marginal product is a crucial concept that reflects the additional output gained from employing one more unit of a variable input. It helps in understanding production efficiency, the relationship between input and output, and the law of diminishing returns.
Detailed
Marginal Product Summary
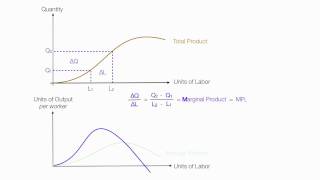
In the context of production theory, the marginal product (MP) of an input is defined as the increase in output that results from using an additional unit of that input, while keeping all other inputs constant. Mathematically, it is represented as:
$$MP = \frac{\Delta TP}{\Delta L}$$
where \(\Delta TP\) represents the change in total product and \(\Delta L\) represents the change in the quantity of the variable input, typically labor. This section explains that marginal product is essential for understanding how input changes affect output and underscores its role in determining the optimal input combinations a firm should use to maximize efficiency and profit.
Additionally, it's important to understand that the marginal product may initially increase as more units of input are employed, but can later decrease due to the law of diminishing marginal returns. This concept is particularly critical when analyzing productivity and efficiency in production processes.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Marginal Product
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Marginal product of an input is defined as the change in output per unit of change in the input when all other inputs are held constant. When capital is held constant, the marginal product of labour is
ΔTP
MP = ----
ΔL
where Δ represents the change of the variable.
Detailed Explanation
Marginal Product (MP) quantifies how much additional output (ΔTP) is produced when one more unit of an input is used while keeping other inputs constant. The formula shows that MP is the change in total product (output) divided by the change in the input used (ΔL). This helps measures productivity for decisions in production.
Examples & Analogies
Think of a baker: if she uses one more cup of flour while keeping everything else the same (like the number of eggs or baking time), the marginal product would tell her how much extra bread she can make with this additional flour. If using the extra flour produces 10 more loaves of bread, then her marginal product of flour would be 10 loaves per cup of flour.
Calculating Marginal Product
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The third column of table 3.2 gives us a numerical example of Marginal Product of labour (with capital fixed at 4) for the production function described in table 3.1. Values in this column are obtained by dividing change in TP by change in L. For example, when L changes from 1 to 2, TP changes from 10 to 24.
MP = (TP at L units) – (TP at L – 1 unit)
Here, Change in TP = 24 - 10 = 14
Change in L = 1
Marginal product of the 2nd unit of labour = 14/1 = 14.
Detailed Explanation
To compute the Marginal Product, we look at the change in total product when an additional unit of labor is added. From the provided example, when the labor increases from 1 unit to 2 units, the total product increases from 10 to 24. Thus, the change in total product (ΔTP) is 14 (24 - 10). Since the change in labor (ΔL) is 1, we find the marginal product as 14. This process helps understand how productive each additional unit of input is.
Examples & Analogies
Take a gardener who plants flowers: if he initially plants 10 flowers and then plants one more, resulting in a total of 12, the increase in flowers (or output) is 2. Thus, the marginal product of that last flower planted would be 2 more flowers. This helps the gardener evaluate the effectiveness of each additional flower he plants.
Marginal Product at Zero Input
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Since inputs cannot take negative values, marginal product is undefined at zero level of input employment. For any level of an input, the sum of marginal products of every preceding unit of that input gives the total product. So total product is the sum of marginal products.
Detailed Explanation
At zero input, the concept of marginal product doesn't apply since there's no output to measure against the input. Therefore, we cannot determine how much more output would result from adding more input when there is none to begin with. Additionally, the total product can be viewed as the accumulation of the marginal products of all inputs, indicating how productive they are as more units are added.
Examples & Analogies
Imagine you are trying to bake a cake but have no ingredients at all: you can't measure how the addition of each ingredient (like flour or sugar) contributes to baking a cake because you're starting from nothing. In order to have productive output, you must first have at least a base level of input.
Relationship between Marginal Product and Total Product
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Average product of an input at any level of employment is the average of all marginal products up to that level. Average and marginal products are often referred to as average and marginal returns, respectively, to the variable input.
Detailed Explanation
The average product (AP) represents the total output (TP) divided by the total quantity of input used. As we increase the input, the marginal product (MP) reflects the additional output produced by the last unit of input. Hence, the relationship is such that if MP is greater than AP, the AP will rise, and if MP is less than AP, the AP will fall. This relationship helps businesses determine the efficiency and effectiveness of their inputs.
Examples & Analogies
Consider a pizza shop: if the chef can make 20 pizzas an hour by himself, and with one assistant they can make 35 pizzas, the marginal product of the assistant is 15 pizzas (the extra pizzas made). If together they produce an average of 17.5 pizzas per chef, the chef’s productivity improved with the assistant, illustrating the concept of returns to input.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Marginal Product: The additional output obtained from increasing a unit of input.
-
Law of Diminishing Returns: A principle that states that after a certain point, additional input yields progressively lower increases in output.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If a baker uses 10 kg of flour to produce 100 loaves of bread, and then adds another kg obtaining 10 more loaves, the marginal product of that additional kg is 10.
-
In a factory, hiring a new employee when production capacity is limited could lead to overcrowding and lower MP as each worker has less space and resources.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When one more worker you apply, a bit more output will fly; but don’t add too many, or productivity may die.
📖 Fascinating Stories
-
Imagine a garden where each gardener can tend many plants, but if too many gardeners crowd in, plants start to get trampled and yield less.
🧠 Other Memory Gems
-
Remember MP as 'More Product' when you add labor until it flops!
🎯 Super Acronyms
MP
- More Power to the additional input
- but watch for the drop (diminishing returns).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Marginal Product
Definition:
The additional output produced when one more unit of a variable input is added, holding all other inputs constant.
-
Term: Total Product
Definition:
The total quantity of output produced by a given combination of inputs.
-
Term: Diminishing Returns
Definition:
A principle stating that as the quantity of one input increases while other inputs are held constant, the marginal product of that input will eventually decline.
-
Term: Variable Input
Definition:
An input whose quantity can be changed in the short run, such as labor.
-
Term: Fixed Input
Definition:
An input whose quantity cannot be changed in the short run, such as capital.