Learn
Games

3.3 - Total Product, Average Product and Marginal Product

Interactive Audio Lesson

Listen to a student-teacher conversation explaining the topic in a relatable way.

Introduction to Total Product

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Welcome, class! Today, we’re diving into Total Product. Can anyone tell me what we mean by Total Product in production?

Student 1
Student 1

Isn’t it the total amount of output produced with a certain level of input?

Teacher
Teacher

Exactly! Total Product (TP) measures the complete output when one variable input changes while others stay constant. Can anyone give me an example?

Student 2
Student 2

Like a farmer increasing labor to harvest more wheat while keeping the land the same?

Teacher
Teacher

Perfect example! Remember, the goal is to understand how varying inputs affect production. Moving on, let’s connect TP with Average Product.

Understanding Average Product

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

So, continuing from Total Product, let’s discuss Average Product (AP). How do you think we define it?

Student 3
Student 3

Is it the output per unit of input?

Teacher
Teacher

Exactly, AP = TP / L. It reflects how efficiently each unit of input contributes to production. Why do you think this is important?

Student 4
Student 4

It helps determine if we’re using inputs efficiently, right?

Teacher
Teacher

That's correct! Efficient input use is critical for maximizing profits. Now, let's look at Marginal Product.

Exploring Marginal Product

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Now we reach Marginal Product (MP). What does it convey?

Student 1
Student 1

It shows the additional output from adding one more unit of input.

Teacher
Teacher

Correct! It’s calculated as the change in TP over change in L. Why is this metric crucial for firms?

Student 3
Student 3

It helps decide if hiring more workers will actually increase output significantly.

Teacher
Teacher

Exactly! Understanding MP is vital for production efficiency and cost management. Let’s summarize what we’ve learned.

Relationships and Implications

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Now, how do Total Product, Average Product, and Marginal Product relate to each other?

Student 4
Student 4

I think as long as MP is greater than AP, AP increases.

Teacher
Teacher

Right! But when MP falls below AP, what happens?

Student 2
Student 2

Then the average product starts to decrease too.

Teacher
Teacher

Excellent! These points reinforce the understanding of production efficacy and optimization. Who can recall the law of diminishing marginal product?

The Law of Diminishing Marginal Product

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

The law of diminishing marginal product states that as you add more units of a variable input, the marginal product eventually decreases. Can anyone explain why this occurs?

Student 3
Student 3

It happens because there’s a limit to how efficiently inputs can work together. Eventually, adding more of one input, like labor, leads to overcrowding.

Teacher
Teacher

Correct! This law is crucial in farm management. Can we think of a scenario where this could apply?

Student 1
Student 1

If a farmer has more workers than land, each worker may contribute less than when there were fewer workers.

Teacher
Teacher

Absolutely! Great job summing things up. Understanding these concepts is essential for firms aiming to optimize production.

Introduction & Overview

Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.

Quick Overview

This section explores the concepts of Total Product, Average Product, and Marginal Product, establishing their significance in understanding the production function and the contributions of variable inputs while other inputs are held constant.

Standard

In this section, we delve into the definitions and calculations of Total Product (TP), Average Product (AP), and Marginal Product (MP). We examine their relationships, how they interact, and the implications of the law of diminishing marginal product. This lays the foundation for understanding efficient production and cost structure in firms.

Detailed

Total Product, Average Product and Marginal Product

In production economics, understanding the output produced by variable inputs while keeping other inputs constant is crucial. Total Product (TP) refers to the total output generated with varying levels of a single input. For instance, in a scenario where capital is held constant, increasing labor input affects output levels.

Definitions

  • Total Product: The aggregate output produced from variable input, calculated when all other inputs are fixed.
  • Average Product (AP): This represents output per unit of variable input and is calculated by dividing total product (TP) by the amount of labor (L): AP = TP/L.
  • Marginal Product (MP): Marginal Product measures the change in total output resulting from a one-unit change in the variable input, calculated as MP = change in TP/change in L.

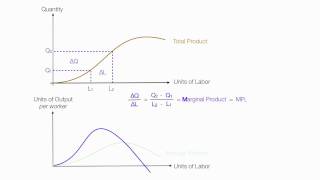
These concepts are linked through the law of diminishing marginal product, illustrating that as more units of a variable input are added, there comes a point where additional input contributes less to production than preceding units, causing MP to decline after a certain point. Graphically, the TP curve is upward sloping, reflecting the increase in output, while both AP and MP typically follow inverse U-shape trends. This informs producers on maximizing output levels efficiently, thereby understanding the cost structure.

Youtube Videos

Total product, marginal product and average product | APⓇ Microeconomics | Khan Academy
Total product, marginal product and average product | APⓇ Microeconomics | Khan Academy
Introduction to Production Introduction (Average Product, Marginal Product, Total Product)
Introduction to Production Introduction (Average Product, Marginal Product, Total Product)
Total product, Average product, Marginal product | Production function | #Part2 #EconomicsAasaanHai
Total product, Average product, Marginal product | Production function | #Part2 #EconomicsAasaanHai
Total Product, Average Product, Marginal Product| (Microeconomics)
Total Product, Average Product, Marginal Product| (Microeconomics)
Total product, Marginal product, and Average product| Microeconomics | Deepti Mahajan
Total product, Marginal product, and Average product| Microeconomics | Deepti Mahajan
Total Product, Marginal Product and Average Product II CLASS 11 MICROECONOMICS II SANYAM BHAYANA
Total Product, Marginal Product and Average Product II CLASS 11 MICROECONOMICS II SANYAM BHAYANA
Relationship Between Average Product And Marginal Product | Production Function | Economics
Relationship Between Average Product And Marginal Product | Production Function | Economics
NCERT Class 12 Microeconomics Chapter 3: Production & Costs (Examrace) | English CUET Economics
NCERT Class 12 Microeconomics Chapter 3: Production & Costs (Examrace) | English CUET Economics
Law of diminishing marginal utility|Economics|Micro Economics
Law of diminishing marginal utility|Economics|Micro Economics
📊 Production & Costs in Economics | Total, Marginal & Average Product Explained! | CUET 2025 🚀📖
📊 Production & Costs in Economics | Total, Marginal & Average Product Explained! | CUET 2025 🚀📖

Audio Book

Dive deep into the subject with an immersive audiobook experience.

Total Product (TP)

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Suppose we vary a single input and keep all other inputs constant. Then for different levels of that input, we get different levels of output. This relationship between the variable input and output, keeping all other inputs constant, is often referred to as Total Product (TP) of the variable input. Let us again look at Table 3.1. Suppose capital is fixed at 4 units. Now in the Table 3.1, we look at the column where capital takes the value 4. As we move down along the column, we get the output values for different values of labour. This is the total product of labour schedule with K = 4. This is also sometimes called total return to or total physical product of the variable input. This is shown again in the second column of table in 3.2.

Detailed Explanation

Total Product (TP) refers to the total output generated by varying one input while keeping all other inputs constant. For example, if a farmer increases the number of hours worked while keeping the size of the field the same, the TP shows how much more crop can be produced. In our table example, with capital fixed at 4 units, we can see how changing the labour input results in different outputs.

Examples & Analogies

Think of Total Product like cooking a dish. If you keep the recipe (the other inputs) the same but change the number of chefs (the variable input), the total amount of food prepared increases as more chefs work.

Average Product (AP)

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Average product is defined as the output per unit of variable input. We calculate it as AP = TP / L, where L is the number of units of the variable input employed. The last column of table 3.2 gives us a numerical example of average product of labour (with capital fixed at 4) for the production function described in table 3.1. Values in this column are obtained by dividing TP (column 2) by L (Column 1).

Detailed Explanation

Average Product (AP) tells us how much output is generated on average for each unit of the variable input used. It is calculated by dividing the Total Product (TP) by the quantity of the variable input used. This measure helps understand the efficiency of the input—if AP is high, it means that each unit of the input contributes significantly to production.

Examples & Analogies

Imagine you have a group of friends helping you with a project. If you produce 100 units of work with 10 friends, your Average Product is 10 units per friend. If you then add more friends and your total production increases but the average starts to drop, it indicates that the additional friends are not as productive due to crowding.

Marginal Product (MP)

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Marginal product of an input is defined as the change in output per unit of change in the input when all other inputs are held constant. When capital is held constant, the marginal product of labour is Change in output / Change in input = ∆TP / ∆L. The third column of table 3.2 gives us a numerical example of Marginal Product of labour (with capital fixed at 4) for the production function described in table 3.1. Values in this column are obtained by dividing change in TP by change in L.

Detailed Explanation

Marginal Product (MP) measures the additional output that results from using one more unit of a variable input, keeping all other inputs constant. For instance, if adding one more worker increases total output significantly, the MP for that worker is high. If output increases only slightly, the MP is low. MP helps firms decide how many units of an input to employ based on the added output they provide.

Examples & Analogies

Think of Marginal Product like adding a new employee to a team. If hiring that employee results in a huge boost in productivity, they have a high MP. If their addition hardly changes the team's output because the team is already at full capacity, their MP is low.

Relationship Between TP, AP, and MP

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Since inputs cannot take negative values, marginal product is undefined at zero level of input employment. For any level of an input, the sum of marginal products of every preceding unit of that input gives the total product. So total product is the sum of marginal products. Average product of an input at any level of employment is the average of all marginal products up to that level. Average and marginal products are often referred to as average and marginal returns, respectively, to the variable input.

Detailed Explanation

The relationship between TP, AP, and MP is essential for understanding productivity. Total Product (TP) is the overall output, Average Product (AP) shows the average efficiency of the input, and Marginal Product (MP) indicates the contribution of each additional unit of input. When MP is greater than AP, it pulls the average up; when MP falls below AP, it drags the average down.

Examples & Analogies

Using a sports analogy, think of TP like the total points scored by a team in a game (TP), AP as the average points scored by each player (AP), and MP as how many points an extra player might contribute (MP). If adding a new player boosts the team's average points per player, they are highly effective; if not, their contribution is minimal.

Definitions & Key Concepts

Learn essential terms and foundational ideas that form the basis of the topic.

Key Concepts

  • Total Product: The total output generated from varying one input while holding others constant.

  • Average Product: Output per unit of input, informing efficiency.

  • Marginal Product: Additional output from adding one more unit of input.

  • Law of Diminishing Marginal Product: As more inputs are added, marginal contributions will decline.

Examples & Real-Life Applications

See how the concepts apply in real-world scenarios to understand their practical implications.

Examples

  • A farmer with fixed land hires more labor, leading to increased initial output but stagnant total output as more workers are added.

  • When labor increases from one to two units, Total Product may increase from 10 to 24, showcasing how input valves affect overall production.

Memory Aids

Use mnemonics, acronyms, or visual cues to help remember key information more easily.

🎵 Rhymes Time

  • In production, products total we seek, each input we tweak, but know this peak! Marginal falls after it first does rise.

📖 Fascinating Stories

  • Once in a field, a farmer hired laborers. At first, productivity soared as he increased the number of workers. However, soon he found they were stepping on each other's toes, and output didn't climb as expected. This story illustrates the law of diminishing returns!

🧠 Other Memory Gems

  • TP, AP, MP - The Three: 'Total increases, Average counts, Marginal shows the extra amount!'

🎯 Super Acronyms

TAM (Total, Average, Marginal) - Remember these key metrics in production!

Flash Cards

Review key concepts with flashcards.

Glossary of Terms

Review the Definitions for terms.

  • Term: Total Product (TP)

    Definition:

    The total quantity of output produced by varying a single input while holding other inputs constant.

  • Term: Average Product (AP)

    Definition:

    Output per unit of variable input, calculated as TP divided by the amount of the variable input.

  • Term: Marginal Product (MP)

    Definition:

    The additional output produced by the last unit of variable input employed, measured as the change in TP per unit increase in the variable input.

  • Term: Law of Diminishing Marginal Product

    Definition:

    A principle stating that as more units of one input are added to a fixed input, the additional output generated by each new unit will eventually decrease.

  • Term: Production Function

    Definition:

    The relationship between inputs used and the output produced in a firm.