EQUIPOTENTIAL SURFACES
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Equipotential Surfaces
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to discuss equipotential surfaces. Does anyone know what we mean by 'equipotential'?

I think it means that the potential energy is the same all over the surface.

That's right! Equipotential surfaces are surfaces where the electric potential remains constant. For a point charge, these surfaces are actually spherical shells. Can anyone tell me why movement along these surfaces requires no work?

Because if the potential is the same, there is no change in potential energy.

Exactly! And since no work is done, the net force must be zero along that path. Let’s remember this with the acronym 'REMOVE' - No Work on Equipotential surfaces!

That's a good way to remember it!

Now, let’s discuss what equipotential surfaces look like among different charge configurations.
Equipotential Surfaces for Point Charges
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

For a single point charge, equipotential surfaces are spherical. Why do you think that is?

Because the potential at a point depends on the distance from the charge.

Exactly! The potential decreases with increase in distance, hence we visualize it as concentric spheres around the charge. This brings up the notation 'PEAR' - Potential Energy Around Radii.

So if we have a positive point charge, the equipotential surfaces are all spherical with increasing radius?

Yes, well put! And they help us understand how electric field lines interact with these surfaces. The field lines are always normal to equipotential surfaces. Can anyone tell me why?

Because if they weren't perpendicular, moving a charge would require work against the electric field.

Perfect! Remember that when analyzing electric fields, the direction of the field gives us insight into potential gradients.
Equipotential Surfaces in Uniform Fields
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s examine equipotential surfaces in a uniform electric field. What can you picture?

I think they would be flat planes rather than curved ones.

Correct! In a uniform electric field, the equipotential surfaces are indeed parallel planes. Let’s remember this with the acronym 'FOLD' - Flat Orientation in Little Distance. Can someone tell me how this relates to the potential difference?

The potential difference between two points would be the same no matter which path you take.

Exactly! The potential difference only depends on the positions of the two points involved. Now let’s discuss the significance of the relationship between the electric field and potential.
Work and Electric Fields
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

What is the fundamental relationship between electric fields and potential differences?

"It's that the electric field is negative the slope of the potential, or
Significance of Equipotential Surfaces
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

In conclusion, equipotential surfaces are not just abstract concepts; they help us understand electric fields and forces in real-world situations like capacitors. Can anyone give an example of where they might apply this concept?

In circuits with capacitors, we need to know how charges move!

Excellent point! Remember, understanding these concepts allows us to predict how systems will behave in the presence of electric fields. Always think about the relationships we've established today as you continue to study.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we explore the concept of equipotential surfaces, which are surfaces where the electric potential remains constant. We discuss how for a point charge, the equipotential surfaces are concentric spheres, while for uniform electric fields, they are parallel planes. The relationship between electric fields and p
Electric Potential l Electrostatics l Ashu Sir #science #physics #electrostaticsotential differences is also established, emphasizing that no work is required to move a charge along an equipotential surface.
Detailed
Equipotential Surfaces
Equipotential surfaces are defined as surfaces where the electric potential is the same at all points. This implies that if a charge is moved along such a surface, no work is required because the potential difference between any two points on the surface is zero. The key points include:
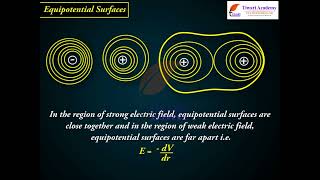
- Equipotential Surfaces for a Point Charge: When considering a single point charge, the equipotential surfaces are spherical shells centered around the charge. The electric field lines emanate radially from the charge, and the field is always normal (perpendicular) to the equipotential surfaces.
- Uniform Electric Field: In a uniform electric field, the equipotential surfaces are parallel planes. For example, if one considers an electric field directed along the x-axis, the equipotential surfaces are infinite planes normal to this direction.
- Work Done and Electric Field Relation: The relationship between the electric field (E) and the potential difference (ΔV) is given by the negative gradient of potential, or mathematically:
\[
|E| = -\frac{\Delta V}{\Delta l}
\]
where Δl is the displacement along the field direction. This means that the electric field points in the direction of greatest decrease of electric potential.
- Consequence for Movement of Charges: As it follows from these definitions, any movement of a charge along an equipotential surface does not require work, which supports the understanding of forces in electrostatics and further emphasizes the conservative nature of electric fields.
Understanding equipotential surfaces is crucial for analyzing electric fields and forces, especially when studying circuits, capacitors, and fields generated by point charges.
Youtube Videos









Key Concepts
-
Equipotential Surface: A surface where the electrical potential is the same at all points.
-
Electric Field: The vector field surrounding electric charges, representing forces on other charges.
-
Potential Difference: The change in potential energy per unit charge between two points in an electric field.
-
Radial Equipotential Surface: Spherical surfaces around a point charge.
Examples & Applications
The concept of equipotential surfaces explains why no work is done when moving charges along these surfaces.
In a uniform electric field, equipotential surfaces are straight, parallel planes.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
No work for a charge to stay, on equipotential, it's just play.
Stories
Imagine a teaching assistant on a mountain where every point has the same energy. Moving him around the mountain requires no energy—this is how equipotential surfaces function.
Memory Tools
Remember PEAR: Potential Energy Around Radii, for spherical equipotential surfaces.
Acronyms
FOLD
Flat Orientation in Little Distance for uniform fields.
Flash Cards
Glossary
- Equipotential Surface
A surface on which the electric potential is the same at every point.
- Electric Field
A region around a charged particle where a force would be experienced by other charged particles.
- Potential Difference
The difference in electrical potential between two points.
- Concentric Spheres
Spheres that share the same center but have different radii.
Reference links
Supplementary resources to enhance your learning experience.
