Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Advantages of Computer Arithmetic
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we're focusing on the advantages of computer arithmetic in system design. One of the key advantages is how it enables efficient hardware design for computations. Can anyone share what that might mean in practice?
It means we can create hardware that performs calculations accurately and quickly!
That's right! Efficient hardware design significantly improves the speed of computations. Additionally, optimization can be targeted based on the specific use case, balancing speed, area, and power. Can anyone think of examples?
Like optimizing a CPU for gaming versus scientific calculations!
Great example! So, we can customize the Arithmetic Logic Units or Floating-Point Units to cater to specific needs. Remember the acronym **ECO** (Efficient, Customized, Optimized) for the advantages. Let's move on to the disadvantages.
Disadvantages of Computer Arithmetic
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's discuss the disadvantages. One significant drawback is that floating-point design is complex and resource-heavy. Does anyone want to elaborate on why that might be the case?
Because managing the precision of floating-point numbers can be really difficult!
Exactly! The complexity increases with the need to handle varying mantissas and exponents. Additionally, arithmetic overflow and underflow must be handled carefully. Why is this important?
Because it can lead to incorrect results if not managed!
Yes, managing these errors is crucial. Lastly, engineers often face trade-offs between accuracy, speed, and silicon area. A good mnemonic here is **TAS** (Trade-off, Accuracy, Speed). Understanding both the advantages and disadvantages helps in designing better systems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section identifies how efficient hardware design and optimization can be achieved through computer arithmetic, while also highlighting the complexity and trade-offs in design, especially regarding floating-point operations and the careful management of arithmetic errors.
Detailed
Advantages and Disadvantages of Computer Arithmetic in System Design
The exploration of computer arithmetic brings both benefits and challenges in system design.
Advantages:
1. Efficient Hardware Design: Computer arithmetic enables the realization of efficient hardware components tailored for specific computational requirements, optimizing performance across various applications.
2. Targeted Optimization Strategies: Designers can focus optimizations based on use cases, balancing speed, area, and power consumption effectively.
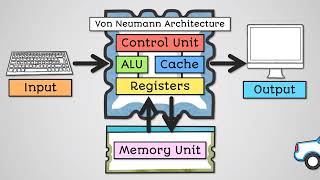
3. Specialized Units: The design of specialized Arithmetic Logic Units (ALUs) and Floating-Point Units (FPUs) allows for advanced computational capabilities that enhance the efficiency and speed of processing.
Disadvantages:
1. Complexity of Floating-Point Designs: Designing floating-point operations is intricate and consumes significant hardware resources, making it a challenging aspect of system architecture.
2. Handling of Overflows/Underflows: Arithmetic operations are prone to errors such as overflow and underflow, which necessitates careful handling to avoid inaccuracies, especially in critical computing tasks.
3. Trade-Offs in Design: Engineers must navigate trade-offs between accuracy, speed, and the physical area on silicon, which can complicate the design process and impact overall system performance.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Advantages of Computer Arithmetic
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β
Advantages:
β Enables efficient hardware design for computation
β Allows optimization based on target use (speed, area, power)
β Facilitates design of specialized ALUs and FPUs
Detailed Explanation
This chunk outlines the key advantages of using computer arithmetic in system design. The first point highlights how computer arithmetic contributes to creating efficient hardware designs, which is crucial for performance. The second point emphasizes that designers can optimize systems according to specific requirements, such as speed for processing speed, minimal area on the chip for space-saving, or low power consumption for energy efficiency. Lastly, the ability to create specialized Arithmetic Logic Units (ALUs) and Floating-Point Units (FPUs) indicates that computer arithmetic allows for tailored solutions that can meet various operational demands.
Examples & Analogies
Imagine designing a custom sports car. Just like engineers optimize every detail for speed, weight, and fuel efficiency, computer architects optimize hardware designs using arithmetic. This means they can create a machine specifically built for fast racing on tracks (high speed), one that saves space and weight (small chip area), or one that can run for longer on less fuel (energy efficiency). Each design serves a different purpose, similar to how different ALUs and FPUs serve specific needs in computing.
Disadvantages of Computer Arithmetic
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Disadvantages:
β Floating-point design is complex and resource-heavy
β Arithmetic overflow/underflow must be handled carefully
β Trade-offs required between accuracy, speed, and silicon area
Detailed Explanation
This chunk discusses the disadvantages associated with computer arithmetic. The first point mentions that designing floating-point arithmetic systems can be complex and requires a lot of resources (like hardware space and power). The second point addresses the challenges of managing arithmetic overflow (when a calculation exceeds the maximum limit) and underflow (when a calculation produces a value closer to zero than can be represented). Finally, it notes that there are often trade-offs in design: achieving the best accuracy may require more processing time and space on the chip, which can complicate design decisions.
Examples & Analogies
Think about cooking a complicated recipe that requires special ingredients. While the end dish might be exquisite (high accuracy), gathering those specialty items takes a lot of time and effort (increased resources), and you may have to make compromises on time or ingredients if you're short on supplies (trade-offs). Similarly, with computer arithmetic, achieving perfect calculations might require advanced setups at the cost of time or device resources, and if you aren't careful, you could end up with incorrect results if you exceed the limits of what your tools can handle (overflow/underflow).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Efficient Hardware Design: Enables the creation of hardware optimized for specific computational tasks.
-
Floating-Point Complexity: Designing floating-point operations is resource-intensive and intricate.
-
Overflow and Underflow: Errors that must be managed to ensure accuracy in calculations.
-
Trade-Offs: Balancing accuracy, speed, and silicon area is critical in system design.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using ALUs to enhance CPU performance in gaming applications can lead to faster calculations.
-
Floating-point arithmetic is essential in scientific computing, where precise calculations are required.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Design well, to speed up the swell, optimize right, and avoid the plight.
π Fascinating Stories
-
Imagine a chef optimizing a recipe. Each ingredient represents a computing aspect: speed, power, or accuracy. Cutting back on one can spoil the dish, just like trade-offs in computer arithmetic.
π§ Other Memory Gems
-
Remember TASE for advantages: Targeted optimization, Accurate results, Speed boost, Efficiency.
π― Super Acronyms
Use **ECO** to recall the advantages
- Efficient design
- Customized use
- Optimized performance.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Arithmetic Logic Unit (ALU)
Definition:
A digital circuit used to perform arithmetic and logical operations.
-
Term: FloatingPoint Unit (FPU)
Definition:
A part of the CPU specialized in handling floating-point arithmetic operations.
-
Term: Overflow
Definition:
A condition that occurs when an arithmetic operation exceeds the maximum limit of the number representation.
-
Term: Underflow
Definition:
A situation where a number is too small to be represented within the number system due to precision limits.
-
Term: Optimization
Definition:
The process of making a system or design as effective or functional as possible.