Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Floating-Point Representation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're exploring floating-point representation, which is essential for handling large and small numbers in computers. Can anyone tell me why this is important?
It's important for calculations in scientific applications!
Exactly! Floating-point helps us avoid overflow or underflow in calculations. Remember, it lets us represent numbers that are either very large or very small efficiently.
What format is typically used for floating-point representation?
The IEEE 754 standard is commonly used. It breaks down the number into a sign bit, an exponent, and a mantissa.
Structure of Floating-Point Numbers
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's dive into how floating-point numbers are structured. Who can tell me what the components of the IEEE 754 format are?
There's the sign bit, exponent, and the mantissa!
Great! The sign bit tells us if the number is negative or positive. The exponent allows for scaling, and the mantissa represents the actual digits of the number. Can anyone remember how many bits are in the single precision format?
It has 32 bits in total, right? 1 for sign, 8 for exponent, and 23 for mantissa.
Exactly! This format allows a wide range of real numbers to be handled effectively.
Examples of Floating-Point Representation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs look at an example. If we take the number -4.25, how would we represent it in IEEE 754 format?
Weβd start with the sign bit of 1 since it's negative.
Right! What about the mantissa?
We would convert 4.25 into binary and find the mantissa!
Nice work! Donβt forget to normalize it and adjust the exponent accordingly. This is a key part of mastering floating-point representation.
Precision and Range
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
One last point to discuss: the range and precision of floating-point numbers. What do these terms mean?
The range is how large or small a number we can represent, and precision refers to how accurate that representation is.
Exactly! The precision is limited by the number of bits in the mantissa. So, when using floating-point, we must balance range and precision.
What happens when we exceed this precision?
Good question! Exceeding precision can lead to rounding errors, which is critical in numerical calculations. Always be cautious with precision in floating-point arithmetic.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Floating-point representation is a standard method for representing real numbers in computers, enabling efficient computation of both large and small values. Focusing on the IEEE 754 standard, this section covers the structure of floating-point numbers, including the sign bit, exponent, and mantissa, along with examples of single precision representation.
Detailed
Floating-Point Representation
Floating-point representation is a crucial concept within computer arithmetic that allows for the representation and manipulation of very large or very small real numbers. This method is particularly important for applications requiring high precision and extensive range, such as scientific computing. The IEEE 754 standard defines the format used for floating-point numbers, which consists of three key components:
- Sign Bit: Indicates whether the number is positive or negative.
- Exponent: Scales the number by powers of two, allowing the representation of very large or small values.
- Mantissa (or Significant): Represents the precision bits of the number.
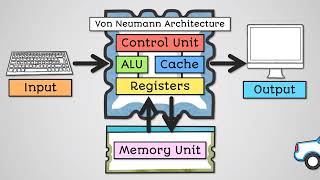
For instance, in the 32-bit single precision format specified by IEEE 754, there is 1 sign bit, 8 bits for the exponent, and 23 bits for the mantissa. The floating-point representation format thus allows computers to perform arithmetic operations on real-world numbers while maintaining a balance between range and precision.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Floating-Point Representation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Represents very large or small real numbers.
β Follows IEEE 754 standard.
Detailed Explanation
Floating-point representation is a method used in computing to represent numbers that are either very large or very small. This is crucial because standard integer representations could not cover the wide range of values needed in various applications, such as scientific computations. To ensure consistency across different computing systems, the IEEE 754 standard was established as a guideline for how these numbers should be formatted and interpreted.
Examples & Analogies
Think of floating-point numbers like a digital clock that can show both very specific times like 0.001 seconds and very broad times like 100,000 seconds. Just as the clock's format allows it to handle a wide range of time values without losing precision, floating-point representation allows computers to cope with a vast range of numeric values.
Format of Floating-Point Numbers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Format: Sign bit + Exponent + Mantissa
β Example: 32-bit single precision (1 + 8 + 23)
Detailed Explanation
Floating-point numbers are typically represented using three primary components: the sign bit, the exponent, and the mantissa (or significand). The sign bit determines if the number is positive or negative. The exponent adjusts the scale of the number, while the mantissa comprises the significant digits of the number. For instance, in a 32-bit single precision format, there's 1 bit for the sign, 8 bits for the exponent, and 23 bits for the mantissa. Together, these allow for a wide range of numbers with varying levels of precision.
Examples & Analogies
Consider a recipe that requires both precise measurements and adjustments; the sign bit is like knowing if you need to add or remove a pinch of salt (positive or negative), the exponent helps you scale your ingredients up or down (like doubling a recipe), and the mantissa ensures that the important flavor components are preserved regardless of how much of each ingredient you're using.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Floating-Point Representation: This system allows computers to perform calculations with very large or very small numbers efficiently.
-
IEEE 754 Standard: The agreed-upon format for representing floating-point numbers across different computer systems.
-
Sign Bit: Indicates if the number is positive or negative.
-
Exponent: The part that determines the scale of the number.
-
Mantissa: Holds the significant digits and precision of the number.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The number -4.25 is represented in IEEE 754 format with a sign bit of 1, an exponent that scales it, and a mantissa that represents the digits.
-
The floating-point representation can efficiently handle calculations like 1.23e10 or 3.45e-5, showing how numbers can have a wide range while maintaining a level of precision.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
The sign bit's zero is bright and clear, a positive number to persevere. A one means negative is here, letβs use the exponent to steer!
π Fascinating Stories
-
Imagine a librarian organizing books. Each sign bit tells whether the book is fiction (positive) or non-fiction (negative), while the exponent helps locate where in the library the book's stored. The mantissa holds the details so you can find that specific book easily.
π§ Other Memory Gems
-
To remember the components: 'Sign, Exponent, Mantissa' - say 'Some Elephants March'!
π― Super Acronyms
Remember 'SEM' for Sign, Exponent, Mantissa.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: FloatingPoint Representation
Definition:
A method of representing real numbers that accommodates a wide range by using a sign bit, exponent, and mantissa.
-
Term: IEEE 754
Definition:
A standardized format for floating-point representation in computers, defining how numbers are stored and manipulated.
-
Term: Sign Bit
Definition:
A single bit in floating-point representation that determines if the number is positive or negative.
-
Term: Exponent
Definition:
Part of a floating-point number that scales the number by powers of two.
-
Term: Mantissa
Definition:
The part of a floating-point number that represents the significant digits.