Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Computer Arithmetic
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Welcome everyone! Today we'll be learning about computer arithmetic. Can anyone tell me what they think computer arithmetic involves?
Isn't it about how computers handle numbers?
Exactly! Computer arithmetic is how numbers are represented and manipulated by hardware. It's crucial for executing operations in CPUs and other digital systems.
So, why is it important for system design?
Great question! Understanding computer arithmetic is essential for optimizing systems. The operations we perform depend heavily on how these numbers are represented.
What types of number representations are we talking about?
We have various representations, such as unsigned and signed binary numbers, as well as fixed-point and floating-point representations. Let's explore these in detail!
Number Representation in Computers
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's dive into number representation. First, who can explain what an unsigned binary number is?
I think it describes non-negative integers using binary.
That's correct! The range for n bits is from 0 to 2^n - 1. Now, how about signed binary numbers?
They can represent both positive and negative values.
Right! There are formats like sign-magnitude and two's complement. Who remembers how to find the two's complement of a number?
You invert the bits and add one!
Exactly! This is a crucial step for subtraction in binary. Moving on, what do we know about fixed-point and floating-point representations?
Fixed-point is for numbers with a fixed number of digits after the binary point, while floating-point can represent very large or small values.
Precisely! Floating-point follows the IEEE 754 standard and includes a sign bit, exponent, and mantissa.
Arithmetic Operations
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's talk about arithmetic operations. What methods do we use for addition and subtraction in binary?
We can use ripple carry adders or carry-lookahead adders.
Right! And for subtraction?
We can subtract using two's complement.
Good! Now, how do we multiply and divide in binary?
Multiplication uses the shift-and-add algorithm, and division can be done using restoring or non-restoring methods.
That's correct! Remember, multiplication is generally faster than division, which is often more complex. Let's review these operations!
Floating-Point Arithmetic
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Next, let's delve into floating-point arithmetic. Why is this topic so crucial in computing?
It allows us to perform operations on very large or very small real numbers.
Exactly! Floating-point numbers are expressed in normalized scientific notation. Can anyone explain how rounding works?
There are different rounding modes, like round to nearest and round toward zero.
Great observation! Handling exceptions like overflow and underflow is also important. What do we use in modern CPUs to process these arithmetic operations?
Floating Point Units (FPUs)!
Hardware Implementation and Optimization Techniques
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Finally, let's discuss the hardware implementation. What components are involved in arithmetic units?
They include adders, multipliers, and dividers.
Correct! Optimization techniques like Carry-Lookahead Adders reduce carry propagation delay. Who remembers other techniques?
Wallace Tree Multipliers help in fast multiplication!
Exactly! Pipelined arithmetic units also increase throughput. Remember that optimizations vary based on speed, area, and power needs.
What are some applications of these techniques?
Applications range from digital signal processing to scientific computing. Understanding these applications helps in designing specialized ALUs.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The principles of computer arithmetic are foundational for effectively designing digital systems. It covers various types of number representation, including unsigned and signed numbers, fixed-point and floating-point formats, and the hardware implementations that support arithmetic operations necessary for CPU, DSP, and embedded systems. Optimization techniques and their applications in domains like digital signal processing and scientific computing are also discussed.
Detailed
Principles of Computer Arithmetic in System Design
Computer arithmetic is a vital area that deals with how numbers are represented and manipulated within digital systems. In this chapter, we delve into various representations of numbers, starting with unsigned binary numbers, which represent non-negative integers ranging from 0 to 2^n - 1. Signed binary numbers can represent both positive and negative integers, employing formats such as sign-magnitude and two's complement. The section also discusses fixed-point and floating-point representations, the latter of which follows the IEEE 754 standard allowing the handling of very large and small real numbers.
Arithmetic operations, including addition, subtraction, multiplication, and division, are critically examined, highlighting methods such as the shift-and-add algorithm for multiplication and the performance of both restoring and non-restoring division. Floating-point arithmetic plays a crucial role in modern computing, requiring specialized hardware components, namely Floating-Point Units (FPUs), to handle operations, exponent alignment, rounding, and exception handling.
The construction and optimization of arithmetic unitsβintegral to the Arithmetic Logic Unit (ALU)βis crucial for achieving efficient hardware design, particularly through techniques like Carry-Lookahead Adders and Wallace Tree Multipliers. Lastly, we explore the implications of computer arithmetic in disciplines such as digital signal processing, embedded systems, graphics processing, and scientific computing, outlining both the advantages and challenges inherent to these methods.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Computer Arithmetic
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Computer arithmetic forms the mathematical backbone of digital systems.
β It deals with how numbers are represented and manipulated by hardware.
β Arithmetic units (ALUs) are essential for executing operations in CPUs, DSPs, and embedded systems.
β Understanding computer arithmetic is key for efficient system design and optimization.
Detailed Explanation
This introduction highlights the fundamental role of computer arithmetic in digital systems. It explains how numbers are represented in binary formats and how these representations facilitate arithmetic operations. The text emphasizes the necessity for Arithmetic Logic Units (ALUs) in performing calculations in various computing environments, such as CPUs and digital signal processors. It also states that a solid understanding of computer arithmetic is crucial for designing efficient systems that can perform optimally.
Examples & Analogies
Think of computer arithmetic like the math you use to manage your finances. Just as you need a solid understanding of numbers and calculations to keep track of your budget, computers need arithmetic to process data efficiently. Like a budget planner (the ALU) that helps execute transactions, compute totals, and manage costs, ALUs execute operations in digital computers.
Number Representation in Computers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Unsigned Binary Numbers
β Represent only non-negative integers.
β Range: 0 to 2^n - 1, where n is the number of bits.
- Signed Binary Numbers
Format Description
Sign-Magnitude MSB = sign bit (0 = +, 1 = β); remaining bits = magnitude
1βs Invert all bits to get negative
Complement
2βs Invert all bits and add 1 (commonly used)
Complement - Fixed-Point Representation
β Used for numbers with fractional parts.
β Binary point is fixed at a specific location.
- Floating-Point Representation
β Represents very large or small real numbers.
β Follows IEEE 754 standard.
β Format: Sign bit + Exponent + Mantissa
β Example: 32-bit single precision (1 + 8 + 23)
Detailed Explanation
This section discusses various ways numbers are represented in computers. It starts with unsigned binary numbers, which can only represent non-negative values. Then, signed binary numbers are introduced, explaining different formats like sign-magnitude and two's complement, essential for representing both positive and negative numbers. The section distinguishes between fixed-point and floating-point representations, where fixed-point is used for numbers with a set number of decimal places and floating-point allows representation of numbers with the flexibility of significant digits and exponent, following IEEE standards.
Examples & Analogies
Consider number representation like addressing different types of jars for your ingredients. Unsigned binary numbers are like jars that can only hold sugar (positive values), while signed binary numbers can hold both sugar and salt (positive and negative values). Fixed-point jars have a fixed sizeβlike jars that can only hold a specific amount of sugar to a certain decimal placeβwhile floating-point jars can expand or contract, like using measuring cups that can handle various amounts of ingredients depending on your recipe.
Arithmetic Operations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Addition and Subtraction
β Performed using ripple carry adders or carry-lookahead adders.
β Subtraction via addition of 2's complement.
β Overflow detection is essential in signed operations.
- Multiplication
β Shift-and-add algorithm for binary multiplication.
β Boothβs Algorithm β Handles signed multiplication efficiently.
β Array multipliers β Hardware implementation for fast multiplication.
- Division
β Performed using restoring or non-restoring division.
β Long division method applied in hardware sequentially.
β Division is slower and more complex than multiplication.
Detailed Explanation
This chunk outlines the fundamental arithmetic operations performed by computers, focusing on addition, subtraction, multiplication, and division. It explains the mechanisms behind addition and subtraction, such as using specific types of adders and 2's complement for subtraction. It goes on to describe multiplication techniques, including the shift-and-add method and Booth's Algorithm for handling signed numbers. Lastly, it discusses division, explaining the restoring and non-restoring methods, as well as the inherent complexity and slower nature of division compared to multiplication.
Examples & Analogies
Imagine you are baking cookiesβaddition and subtraction are like mixing ingredients together and removing some if you've added too much. Multiplication is like doubling or tripling your recipe to make more batches efficiently, just as a skilled baker uses methods to calculate ingredients faster. Division is akin to splitting a large batch into smaller portions to serveβit's generally more time-consuming than simply mixing ingredients, as it requires careful measurement.
Floating-Point Arithmetic
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Involves operations on normalized scientific notation.
β Requires exponent alignment, mantissa operations, and normalization.
β Handles rounding modes and exceptions (overflow, underflow, NaN).
β Implemented using FPU (Floating-Point Unit) in modern CPUs.
Detailed Explanation
This section describes floating-point arithmetic, which enables efficient processing of very large or small numbers through normalized scientific notation. It highlights the need for exponent alignment to ensure consistency in calculations. The section also covers the importance of mantissa operations and normalization to maintain accuracy. Additionally, it touches on various rounding modes and exceptions that may arise, like overflow or underflow, and introduces the Floating-Point Unit (FPU) as a dedicated hardware component that handles these operations in modern CPUs.
Examples & Analogies
Think of floating-point arithmetic like managing large sums of money in different currencies. Just as you must align currency values (exponent alignment) and correctly convert amounts (mantissa operations), floating-point systems work to ensure accurate calculations for large or small values. When you're rounding prices or adjusting for currency fluctuations (handling exceptions), having a specialized currency converter (the FPU) makes everything smoother and more efficient.
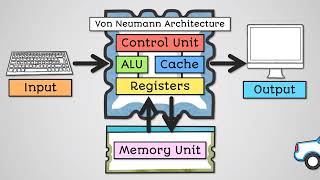
Hardware Implementation of Arithmetic Units
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Arithmetic units are part of the ALU (Arithmetic Logic Unit).
β Designed to support:
β Integer arithmetic
β Floating-point arithmetic
β Logic operations (AND, OR, XOR)
β Shift operations
Unit Function
Adder/Subtractor Basic integer math
Multiplier Fast multiplication using combinational logic
Divider Iterative or combinational approach
FPU IEEE 754 operations, rounding, exceptions
Detailed Explanation
This chunk explains the hardware aspect of arithmetic operations, specifically focusing on the role of the Arithmetic Logic Unit (ALU). It details the types of arithmetic supported by ALUs, including basic integer and floating-point operations along with logical operations and shifting. Individual units within the ALU, such as adder/subtractors for basic math, multipliers for quick calculations, and dividers for handling division are briefly described, pointing out their respective functions.
Examples & Analogies
Consider the ALU as a well-equipped kitchen where different cooking stations handle specific tasks. The adder/subtractor is like the station where you measure and mix ingredients, the multiplier acts like a rapid-fryer that quickly prepares larger batches, and the divider is like the cutting board, ensuring portions are evenly distributed. Each station specializes in an individual task but contributes to creating a delicious dishβmuch like how each arithmetic unit works together within the ALU to process data efficiently.
Optimization Techniques in Arithmetic Logic
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Carry-Lookahead Adders (CLA) β Reduces carry propagation delay.
β Wallace Tree Multipliers β Parallel reduction for faster results.
β Pipelined Arithmetic Units β Increases throughput in floating-point intensive tasks.
β Bit-serial vs. Bit-parallel Design β Trade-off between speed and area.
Detailed Explanation
This chunk discusses various optimization techniques used in arithmetic logic to enhance performance. Carry-Lookahead Adders (CLA) are introduced as a method to minimize delays caused by carry propagation during addition operations. Wallace Tree Multipliers optimize the multiplication process by utilizing a parallel reduction technique to speed up calculations. Pipelined Arithmetic Units are mentioned as a way to enhance throughput during demanding floating-point operations. Finally, the trade-offs between bit-serial and bit-parallel designs highlight the considerations of speed versus area needed in hardware design.
Examples & Analogies
Think about optimizing a factory production line. Using a CLA is like implementing a conveyor belt that allows multiple stations to work simultaneously, reducing delays. Wallace Tree Multipliers act like adding extra workers to tackle more tasks at once, ultimately making the processes faster. Pipelining is similar to having workers focus on different parts of the same task simultaneously to expedite the entire operation. Finally, choosing between bit-serial and bit-parallel is akin to deciding whether to produce one product at a time (slower but requires less space) versus mass-producing many products at once (quicker but needs more space).
Applications in System Design
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Computer arithmetic is critical in various domains:
β Digital Signal Processing (DSP) β Filters, FFTs, image/audio processing
β Embedded Systems β Sensor data processing, control systems
β Graphics Processing Units (GPUs) β Matrix and vector operations
β Cryptographic Systems β Modular arithmetic, large integer operations
β Scientific Computing β Precision-intensive floating-point math
Detailed Explanation
This chunk outlines the various fields where computer arithmetic plays a vital role. It underscores its importance in digital signal processing for managing audio and visual data and its critical function in embedded systems for processing sensor data. The section emphasizes the reliance on arithmetic in graphics processing, cryptographic systems for secure communication, and scientific computing, where accuracy is paramount for complex calculations.
Examples & Analogies
Consider computer arithmetic as the invisible backbone of modern technology. Just like a solid foundation supports a house (ensuring it remains stable), computer arithmetic supports diverse applications in our daily lives. When you listen to your favorite song (DSP), use a smart home device (embedded systems), manipulate images on a computer (GPUs), send secure messages (cryptography), or compute scientific data (scientific computing), it's the effective arithmetic behind the scenes ensuring functionality and accuracy.
Advantages and Disadvantages of Computer Arithmetic
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Advantages:
β Enables efficient hardware design for computation
β Allows optimization based on target use (speed, area, power)
β Facilitates design of specialized ALUs and FPUs
β Disadvantages:
β Floating-point design is complex and resource-heavy
β Arithmetic overflow/underflow must be handled carefully
β Trade-offs required between accuracy, speed, and silicon area
Detailed Explanation
This chunk presents the pros and cons of computer arithmetic. The advantages highlight how it leads to more efficient hardware designs, allows for optimization based on specific goals, and supports the development of specialized units like ALUs and FPUs tailored for different tasks. Conversely, the disadvantages include the complexity of floating-point designs, potential overflow or underflow issues that must be carefully managed, and the need for trade-offs between accuracy, speed, and the physical space on silicon chips.
Examples & Analogies
Think of the advantages as the perks of having a high-performance vehicle designed for speed and efficiency. You get faster transportation and better fuel management for your needs. However, there are also disadvantages, such as higher maintenance costs and risks of breakdowns (the complexity of floating-point design and potential overflow). Itβs similar to choosing between a well-optimized sports car (efficient hardware) and a family vehicleβeach serves different purposes and comes with its own trade-offs.
Summary of Key Concepts
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Computer arithmetic underpins all mathematical processing in CPUs.
β Includes number representation, addition, subtraction, multiplication, and division.
β Floating-point operations are standardized by IEEE 754.
β Hardware optimization techniques like CLA and pipelining improve arithmetic unit performance.
β Arithmetic logic is widely used across embedded, DSP, GPU, and scientific applications.
Detailed Explanation
The summary reiterates the essential role of computer arithmetic in processing information within CPUs. It encapsulates key topics covered in the section, such as the various number representations and arithmetic operations essential for computational tasks. The mention of IEEE 754 emphasizes the importance of standardized floating-point operations for consistency. Additionally, it points out that hardware optimization techniques, including CLA and pipelining, significantly enhance the performance of arithmetic units used in numerous applications across different fields.
Examples & Analogies
This summary serves as the conclusion of a comprehensive learning journey. Imagine it as the end of a cooking class where you've learned about various cuisines (number representations), the techniques for mixing and cooking ingredients (arithmetic operations), and the standard recipes you can rely on (IEEE 754). You now have a toolkit to make delicious meals simplified through efficient cooking techniques (hardware optimization) that can be applied in a wide range of dining experiences (applications in diverse fields).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Unsigned Binary Numbers: Represent only non-negative integers, ranging from 0 to 2^n - 1.
-
Signed Binary Numbers: Can represent both positive and negative integers using sign-magnitude or two's complement.
-
Fixed-Point Representation: Represents numbers with a fixed number of digits after the binary point.
-
Floating-Point Representation: Allows representation of very large or small real numbers and follows IEEE 754 standard.
-
Arithmetic Operations: Includes addition, subtraction, multiplication, and division using specialized hardware implementations.
-
Optimization Techniques: Such as Carry-Lookahead Adders and Wallace Tree Multipliers, are essential for efficient arithmetic unit performance.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For unsigned binary, a 4-bit representation has a range from 0 (0000) to 15 (1111).
-
In two's complement, the binary number 1110 represents -2 in a system with 4 bits.
-
In floating-point representation, the number 0.15625 can be expressed in IEEE 754 format as 0 01111111 01010000000000000000000 in binary.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
In binary, there's a way to play, signed has a sign, while unsigned stays.
π Fascinating Stories
-
Once upon a time in a digital land, numbers danced between signs, both grand and bland. Unsigned flaunted non-negatives, while signed took turns, in negatives and positives, as knowledge burns.
π§ Other Memory Gems
-
Remember 'Fifth FLESH': Fixed-point represents fixed fractions, Floating-point allows for a range. Both relevant in operations of computers.
π― Super Acronyms
FRAC for Floating-point
- F: - Format
- R: - Range
- A: - Arithmetic
- C: - Conversion!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Arithmetic Logic Unit (ALU)
Definition:
A hardware component that performs arithmetic and logical operations.
-
Term: Floating Point Unit (FPU)
Definition:
A specialized processor to handle floating-point arithmetic operations.
-
Term: IEEE 754
Definition:
A standard for floating-point arithmetic used in computers.
-
Term: Two's Complement
Definition:
A method for representing signed integers in binary.
-
Term: Signed Binary Numbers
Definition:
Binary numbers that can represent both positive and negative values.
-
Term: Unsigned Binary Numbers
Definition:
Binary numbers that represent only non-negative integers.
-
Term: Fixed Point Representation
Definition:
A method of representing numbers with a fixed number of decimal places.
-
Term: Floating Point Representation
Definition:
A method to represent real numbers to allow for a wide range of values.
-
Term: Optimization Techniques
Definition:
Methods used to enhance performance and efficiency in hardware.