Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fixed-Point Representation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we'll explore fixed-point representation. This is important for representing numbers that include fractional parts. Can anyone define what fixed-point representation means?
Is it a way to represent numbers by fixing the binary point in a certain place?
Exactly! The binary point is fixed, meaning we designate where the fractional part starts. This helps in computations that involve both whole numbers and fractions.
Why do we use fixed-point instead of floating-point?
Great question! Fixed-point is simpler and requires fewer resources than floating-point, making it faster for certain applications. Remember, fixed = predictable speed!
Structure of Fixed-Point Numbers
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's talk about how fixed-point numbers are structured. Can anyone tell me how many bits are typically used?
Is it a fixed number of bits divided between the whole and fractional parts?
That's correct! For example, if we have a total of 16 bits, we might have 8 bits for the integer part and 8 bits for the fractional. This determines how precise our representation can be.
So if we move the binary point left, does that affect the value?
Yes! Moving the binary point alters the magnitude of the number significantly. Itβs important to maintain it at the correct position for accurate results.
Applications of Fixed-Point Representation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Can anyone think of where fixed-point representation might be used in real life?
Maybe in digital audio processing?
Exactly! It's widely used in digital signal processing, like audio signals, where precise calculations are crucial but dependability and speed are also important.
What about in video games?
Absolutely! Fixed-point is often used in graphics calculations where performance is prioritized. Just remember: Speed is key!
Advantages and Limitations of Fixed-Point Representation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's discuss the advantages of fixed-point representation. What are some benefits you can think of?
Itβs faster and consumes less space than floating point, right?
Exactly! It offers speed and efficiency. But what might be a downside?
It has a limited range?
Exactly right! There's a finite number it can represent; if you exceed that number, you might encounter overflow.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Fixed-point representation allows computers to handle numbers that have fractions by placing the binary point at a predetermined location within the binary representation, facilitating simpler calculations for certain applications compared to floating-point representation.
Detailed
Fixed-Point Representation
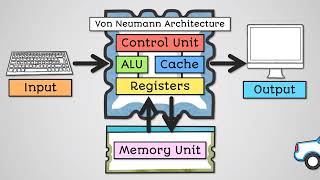
Fixed-point representation is a method for encoding real numbers in a format suitable for use in digital systems, particularly when handling numbers with fractional components. In this system, the binary point (analogous to the decimal point) is fixed at a designated location within the bit sequence, enabling the representation of fractional values while leveraging integer arithmetic for computational operations.
Key Highlights:
- Definition: In fixed-point representation, a fixed number of bits are allocated for both the integer and fractional part of the number, making it easier to perform arithmetic operations without needing complex calculations typical of floating-point systems.
- Binary Point: The location of the binary point is predetermined, determining how many bits are allocated to the integer versus the fractional part.
- Range: The range of values that can be represented depends on the number of bits and the position of the binary point, allowing for efficient representational accuracy within a limited range of fixed values.
- Applications: Commonly used in applications that require predictable and rapid calculations, such as digital signal processing (DSP) and certain embedded systems where performance and precision are critical.
Significance: Understanding fixed-point representation is essential for designing efficient systems that require precise arithmetic without the overhead of managing floating-point numbers.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Fixed-Point Representation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Used for numbers with fractional parts.
β Binary point is fixed at a specific location.
Detailed Explanation
Fixed-point representation is used in digital systems to handle numbers that have fractional parts, making it essential for calculations that require precision, such as in financial transactions or scientific computations. In fixed-point representation, a 'binary point'βwhich serves the same purpose as a decimal point in decimal numbersβis placed at a predetermined position in the binary number. This means that the number of bits assigned to the integer and fractional parts is fixed, thereby defining how accurately we can represent values.
Examples & Analogies
Imagine you're setting the temperature on a thermostat. If you're limited to only using whole numbers, you might set it to 70 degrees without considering the half degrees (like 70.5), which can be problematic for precise temperature control. Fixed-point representation allows you to account for these fractional values, similar to how you might adjust the thermostat to 70.5 degrees for a more comfortable temperature.
Application of Fixed-Point Representation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Fixed-point representation can be used in various applications, such as:
1. Embedded Systems: Handling sensor readings, control loops.
2. Digital Signal Processing: Audio and video data processing tasks.
3. Finance: Accurate representation of monetary values to avoid rounding errors.
Detailed Explanation
Fixed-point representation is especially useful in embedded systems, where resources are limited and real-time processing is crucial. For example, when working with sensor readings in a control loop, using fixed-point arithmetic ensures that the calculations remain fast and energy-efficient. In the context of Digital Signal Processing (DSP), fixed-point representation allows audio and video data to be processed efficiently without the computational overhead of floating-point arithmetic. In finance, fixed-point helps maintain accuracy in monetary calculations, preventing rounding errors that could lead to financial discrepancies.
Examples & Analogies
Think of fixed-point representation in financial settings like using a cash register. If the register can only display whole dollar amounts, it might not accurately reflect the pennies. However, when you account for dollars and cents accurately using fixed-point representation, you avoid issues like having too little or too much money at the end of the day.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Fixed-Point Representation: A system for encoding real numbers where the binary point is fixed at a predetermined position.
-
Binary Point: The point in the binary representation that separates the integer from the fractional part.
-
Precision: The number of bits allocated to represent the fractional part affects the representation's accuracy.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A fixed-point representation using 16 bits can assign 8 bits to the integer part and 8 bits to the fractional part, allowing representation of values like 12.375.
-
In a fixed-point representation, the number 00000001.00000000 represents the integer 1, while 00000000.00000001 represents the fraction 0.00000001.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
When fractions you need, fixed-point will lead, with binary fixed just like a bead!
π Fascinating Stories
-
Imagine a baker measuring flour. He marks the jar where he stops at half. This is the fixed point! When he adds a pinch, he knows he can precisely measure it.
π§ Other Memory Gems
-
FRACTION β Fixed Representation Always Cleared for TImes of Omission of Numbers.
π― Super Acronyms
FIXED β Fixed Integer eXecution with Efficient Division.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: FixedPoint Representation
Definition:
A method of representing real numbers in computers where the binary point is fixed at a certain position.
-
Term: Binary Point
Definition:
The point in a binary number that separates the integer part from the fractional part.
-
Term: Fractional Part
Definition:
The component of a number that represents values less than one.
-
Term: Integer Part
Definition:
The whole number component in a fixed-point representation.
-
Term: Arithmetic Overflow
Definition:
An error that occurs when a calculation exceeds the maximum limit of number representation.