Summary of Key Concepts
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Importance of Computer Arithmetic
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we'll explore why computer arithmetic is essential for digital systems. Can anyone tell me what computer arithmetic involves?

It deals with how numbers are represented and manipulated, right?

Exactly! It's fundamental for all the calculations CPUs perform. Why do you think efficient arithmetic is crucial for system design?

Because it affects speed and accuracy in computations?

Correct! Let’s remember this with the acronym 'EAS' - Efficiency, Accuracy, Speed. Now, let's explore different number representations.
Number Representation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

There are various methods to represent numbers—can anyone name a few?

Unsigned and signed binary, right?

Correct! Unsigned binary represents only positive integers, while signed binary can represent both positive and negative numbers. Can you explain why we might use two's complement?

It's useful because it simplifies subtraction to addition!

Exactly! Also, don't forget about floating-point representation for large numbers. A good mnemonic to remember this is 'SEM' for Sign, Exponent, and Mantissa.
Arithmetic Operations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's shift our focus to arithmetic operations. What are the basic operations we perform in computer arithmetic?

Addition, subtraction, multiplication, and division!

Great! For addition in binary, what's a common method used?

Ripple carry adder! But isn't carry-lookahead faster?

Yes! It reduces the delay caused by carry propagation. For remembering these, think 'RAP'—Ripple, Add, Pipelining.
Floating-Point Arithmetic
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s go deeper into floating-point arithmetic. Why is it standardized by IEEE 754?

To ensure consistency across different systems?

Exactly! And it helps with handling rounding and exceptions too. Can anyone summarize what happens during floating-point operations?

We align the exponents, perform mantissa operations, and then normalize!

Perfect! Remember the acronym 'EOM'—Exponent, Operations, Normalize. Let’s conclude by discussing the optimization techniques.
Hardware Optimization Techniques
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Optimization is crucial to boost the performance of arithmetic units. What techniques have we discussed?

Carry-lookahead adders and Wallace tree multipliers!

Great! Why would we opt for pipelined architectures?

They improve throughput during floating-point intensive tasks.

Exactly! Pipelining allows us to perform multiple instructions simultaneously. Remember our mnemonic 'GASP' for Gain, Accuracy, Speed, Performance to keep this fresh!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The summary encapsulates the essential role of computer arithmetic in digital systems, covering methods of number representation, key arithmetic operations, and the significance of optimization techniques to enhance performance in CPUs and other digital processors.
Detailed
Summary of Key Concepts
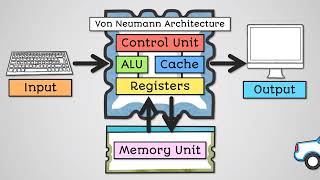
Computer arithmetic is a critical component that underpins mathematical processes in CPUs and other digital systems. It involves a variety of methodologies for number representation, such as unsigned and signed binary numbers, fixed-point, and floating-point representation. Key arithmetic operations include addition, subtraction, multiplication, and division, with techniques such as 2's complement for signed operations and specific algorithms for efficient multiplication and division. The importance of IEEE 754 standards for floating-point operations is highlighted, providing a consistent framework for handling very large or very small numbers.
Moreover, the section elaborates on optimization techniques such as Carry-Lookahead Adders and pipelined architectures, which significantly improve the performance of arithmetic units. These concepts find extensive applications in diverse fields, including Digital Signal Processing (DSP), embedded systems, and scientific computing, thus showcasing the integral role of efficient computer arithmetic in system design.
Youtube Videos


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Foundation of Computer Arithmetic
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
● Computer arithmetic underpins all mathematical processing in CPUs.
Detailed Explanation
Computer arithmetic is the essential mathematical foundation that allows a computer's processor to perform calculations. Without these arithmetic operations, CPUs would not be able to carry out tasks such as addition, subtraction, multiplication, or division, which are crucial for executing programs and applications. Every mathematical operation performed by a computer, whether it's processing data or running algorithms, relies on correct and efficient arithmetic calculations.
Examples & Analogies
Think of computer arithmetic like the basic math skills we need in everyday life. Just like we need to add, subtract, multiply, and divide to manage our finances, plan our schedules, or cook recipes, computers need these arithmetic operations to process information and execute commands. If you give a computer a task that requires calculations—like finding the total cost of items in a shopping cart—it must use computer arithmetic to perform that task correctly.
Key Arithmetic Operations
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
● Includes number representation, addition, subtraction, multiplication, and division.
Detailed Explanation
In computer systems, several key arithmetic operations are vital for processing data. Number representation allows the computer to understand how to encode numbers in binary form, whether they're whole numbers or decimals. Addition and subtraction are fundamental operations carried out by the CPU's arithmetic logic unit (ALU), while multiplication and division handle more complex calculations. Each operation uses different algorithms and methods to achieve accurate results, which are critical for the overall functionality of software and hardware systems.
Examples & Analogies
Consider a calculator as a simple analogy for these operations. Just as a calculator uses algorithms to add, subtract, multiply, and divide numbers, a computer utilizes these operations to perform calculations it needs to run software applications. For instance, when you enter numbers into a calculator, it processes these through its hardware to return the correct results, similar to how a computer's ALU works with binary numbers to compute results.
Standardization of Floating-Point Operations
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
● Floating-point operations are standardized by IEEE 754.
Detailed Explanation
Floating-point operations are crucial for performing calculations with very large or very small real numbers. The IEEE 754 standard defines how these numbers should be represented and processed in computer systems. This standardization ensures that all computers perform floating-point calculations consistently, allowing for compatibility across different platforms and applications. Understanding this standard is important for developers, engineers, and anyone involved in programming or system design, as it impacts the precision and performance of computations.
Examples & Analogies
Imagine measuring ingredients for a recipe using different units like cups, tablespoons, and teaspoons. The IEEE 754 standard is like adopting a universal measurement system in cooking. No matter where you are or who you ask, everyone understands how to measure ingredients in a consistent way. In the context of computing, this means that no matter which computer you use, you can expect floating-point calculations to be precise and consistent, much like knowing that 1 cup equals 16 tablespoons, regardless of the measuring spoons you have.
Performance Optimization Techniques
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
● Hardware optimization techniques like CLA and pipelining improve arithmetic unit performance.
Detailed Explanation
To enhance the efficiency of arithmetic units within CPUs, various optimization techniques are employed. Carry-Lookahead Adders (CLA) are designed to minimize the time taken for addition operations by predicting carry bits in advance, thus speeding up computations. Pipelining, on the other hand, allows multiple arithmetic operations to be processed simultaneously, enhancing throughput and resulting in faster overall computation. These techniques are critical for modern processors to perform complex calculations and tasks quickly and efficiently.
Examples & Analogies
Think of performance optimization in computing like optimizing a production line in a factory. In a well-organized factory, various tasks happen simultaneously to boost productivity; for instance, some workers might assemble parts while others package finished products. Similarly, pipelining in CPUs allows different stages of arithmetic operations to occur at once, greatly increasing efficiency. CLA can be compared to a factory worker who can execute their tasks faster by anticipating future steps in the assembly line, thereby reducing delays and improving overall speed.
Diverse Applications of Arithmetic Logic
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
● Arithmetic logic is widely used across embedded, DSP, GPU, and scientific applications.
Detailed Explanation
Arithmetic logic plays a crucial role in a wide range of applications, from simple embedded systems to complex digital signal processing (DSP) projects, graphics processing units (GPUs), and scientific computing tasks. Each of these domains relies heavily on efficient arithmetic operations to handle computations, process data, and facilitate control systems. Understanding the utilization of arithmetic logic in various fields is essential for recognizing how crucial these operations are in modern technology.
Examples & Analogies
Consider arithmetic logic like the foundation of a building. Just as no matter how beautiful or advanced the structure is, it needs a solid foundation to stand firm, technologies in DSP, GPUs, and scientific computing all rely on strong arithmetic logic to function effectively. For example, when rendering graphics in a video game, GPUs perform thousands of arithmetic operations each second to create smooth and realistic images. Without reliable arithmetic logic, both the graphics and the processing wouldn't be possible.
Key Concepts
-
Computer Arithmetic: The fundamental practices of number representation and manipulation in digital systems.
-
IEEE 754: A standard for floating-point arithmetic that ensures consistency in representation.
-
Arithmetic Operations: Basic mathematical operations including addition, subtraction, multiplication, and division performed by the CPU.
Examples & Applications
An example of unsigned binary representation using 4 bits can represent the numbers 0 to 15.
The two's complement of -3 in 4 bits is represented as 1101.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In computers, we add with glee, arithmetic makes math easy as can be!
Stories
Imagine a world where numbers dance—unsigned, signed, floating freely. They meet in a CPU's brain, where arithmetic helps them gain.
Memory Tools
'EOM' - Remember Exponent, Operations, and Normalize for floating-point processes.
Acronyms
GASP – Gain, Accuracy, Speed, Performance for hardware optimizations.
Flash Cards
Glossary
- Computer Arithmetic
The branch of computer science that focuses on how numbers are represented and manipulated in digital systems.
- IEEE 754
A standard for representing floating-point numbers which ensures consistency across different computing platforms.
- FloatingPoint Representation
A method of representing real numbers that can accommodate a large range of values by using a sign bit, exponent, and mantissa.
- CarryLookahead Adder
An adder that improves speed by reducing the time needed to calculate carry bits.
- SignMagnitude Representation
A method of representing signed integers where the first bit indicates the sign of the number.
Reference links
Supplementary resources to enhance your learning experience.
