Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Carry-Lookahead Adders (CLA)
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're focusing on a crucial optimization technique called Carry-Lookahead Adders, or CLA. Can anyone tell me why carry propagation can be a problem in traditional binary addition?
Well, I think the carry can take time to propagate through multiple bits, which slows down the addition.
Exactly! The CLA addresses this by calculating carry signals in advance, which minimizes delays. The acronym CLA can help you remember its purpose: Carry-Lookahead means anticipating carries for speed. Let's try some examples where CLAs outperform traditional adders. What do you think this results in for overall system performance?
I guess it would allow the CPU to perform calculations faster?
That's right! This speed is crucial in applications requiring real-time processing. Letβs move on to the next technique.
So, using CLAs can significantly enhance performance in arithmetic logic?
Absolutely! In summary, CLAs reduce propagation delays, boosting addition rates and overall performance in arithmetic operations.
Wallace Tree Multipliers
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Next, letβs discuss Wallace Tree Multipliers, a fascinating optimization for multiplication. Who wants to share what they know about how traditional multipliers work?
Traditional multipliers do a lot of sequential addition and shifting, which can be slow.
Right again! The Wallace Tree method structures the multiplication process in a tree fashion to parallelize the addition of partial products. Can anyone explain why this might be advantageous?
It sounds like the parallelization would reduce the time it takes to multiply large numbers.
Exactly! With the Wallace Tree structure, we reduce the total computation time. Remember, Wallace Tree = Fast Multiplication! Letβs think about how this speeds up operations across different applications. Can anyone suggest where such efficiency would be particularly vital?
In video processing or real-time graphics rendering, right?
Spot on! The need for speed in those domains is crucial. So, in summary, Wallace Trees effectively speed up multiplication by using parallel processing of partial sums.
Pipelined Arithmetic Units
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs move to pipelined arithmetic units, another key technique for optimization. Pipelining is where multiple stages of processing occur simultaneously. What do you think this could do for arithmetic operations?
It must speed up processing because while one operation is finishing, others can start.
Precisely! Pipelining can greatly increase throughput, especially for tasks with repetitive calculation patterns like floating-point operations. Remember: Pipelined = More Throughput! Can anyone think of scenarios in computing where this would be greatly beneficial?
In digital signal processing, where multiple calculations on data streams happen?
Exactly! In these cases, pipelining allows systems to maintain a steady flow of operations. So, in summary, pipelined arithmetic units enhance throughput by allowing overlapping execution of multiple tasks.
Bit-Serial vs. Bit-Parallel Design Choices
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Lastly, letβs consider the trade-offs between bit-serial and bit-parallel designs. Can someone summarize what we would consider in choosing between these designs?
I think bit-parallel designs are faster but also need more hardware space?
Correct! Bit-parallel designs indeed execute operations more quickly due to simultaneous processing of bits but at the expense of extra area on the chip. What about bit-serial designs?
They might save on space but take longer to complete operations, right?
Exactly! Itβs about balancing speed and area. So, when designing an arithmetic logic unit, remember: Speed vs. Area is key. In summary, choosing between bit-serial and bit-parallel designs involves understanding the importance of speed and space in your specific application.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section highlights specific techniques, such as Carry-Lookahead Adders (CLA), Wallace Tree multipliers, pipelined arithmetic units, and trade-offs between bit-serial and bit-parallel designs, all aimed at improving computational efficiency in hardware implementations.
Detailed
Optimization Techniques in Arithmetic Logic
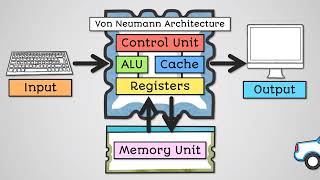
In modern computing, optimization techniques in arithmetic logic are essential for improving performance, especially in resource-intensive applications. This section explores several prominent methods:
- Carry-Lookahead Adders (CLA): This technique minimizes the carry propagation delay that arises during the execution of addition operations, enabling faster computations in arithmetic units.
- Wallace Tree Multipliers: By employing a parallel reduction approach, this method effectively speeds up multiplication processes by arranging the partial products in a tree-like structure, which is more efficient than traditional methods.
- Pipelined Arithmetic Units: Pipelining allows multiple instruction stages to be processed simultaneously, significantly increasing the throughput of floating-point operations and reducing execution time in high-demand scenarios.
- Bit-Serial vs. Bit-Parallel Design: This section also discusses the trade-offs involved in choosing between bit-serial and bit-parallel architectures, emphasizing that while bit-parallel designs offer higher speed, they require more silicon area compared to bit-serial units, which can be slower but more area-efficient.
Overall, these optimization techniques are crucial for improving the efficiency of arithmetic logic units in digital systems, directly impacting performance metrics such as speed, area, and power consumption.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Carry-Lookahead Adders (CLA)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Carry-Lookahead Adders (CLA) β Reduces carry propagation delay.
Detailed Explanation
Carry-Lookahead Adders are designed to speed up the process of binary addition. In a traditional adder, the carry from one bit must be calculated before it can be used in the next bitβs addition, which can lead to delays as the number of bits increases. CLA minimizes this delay by 'looking ahead' to determine whether a carry will occur for each bit position, allowing it to compute carries in parallel rather than sequentially.
Examples & Analogies
Imagine a relay race where each runner must wait for the previous runner to finish before they can start. This waiting slows down the race. A CLA is like a race where all runners start at the same time, each knowing if they need to pass the baton to the next runner based on predictions, thus speeding up the overall process.
Wallace Tree Multipliers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Wallace Tree Multipliers β Parallel reduction for faster results.
Detailed Explanation
Wallace Tree Multipliers are used to perform multiplication quickly by reducing the number of addition operations needed. Instead of adding each partial product in sequence, Wallace Trees organize the addition of these products in a parallel structure. This method allows for faster calculations, especially for larger numbers, by combining several addition stages into one.
Examples & Analogies
Think of it like a group of chefs working in a kitchen. Instead of each chef preparing their dish one after another, they work on different parts of the meal simultaneously. This parallel processing helps them complete the meal much faster than if they worked sequentially.
Pipelined Arithmetic Units
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Pipelined Arithmetic Units β Increases throughput in floating-point intensive tasks.
Detailed Explanation
Pipelined Arithmetic Units are specialized hardware designs that allow multiple arithmetic operations to be processed in a staggered manner. By breaking down the operations into smaller stages (like an assembly line), different parts of multiple calculations can be done simultaneously. This increases the overall throughput of arithmetic operations, which is particularly beneficial in applications requiring heavy floating-point calculations, such as graphics processing.
Examples & Analogies
Imagine a car manufacturing plant where different sections of the assembly line handle different tasks. Each car goes through the line at various stages (like attaching the doors, painting, etc.). While one car is getting painted, another can have its wheels attached, allowing many cars to be completed faster than if each car went through the entire process without interruption.
Bit-serial vs. Bit-parallel Design
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Bit-serial vs. Bit-parallel Design β Trade-off between speed and area.
Detailed Explanation
The design of arithmetic operations can either be bit-serial or bit-parallel. Bit-serial designs process one bit of data at a time, which can save space (area) in hardware but generally slows down computation. Bit-parallel designs, on the other hand, handle multiple bits simultaneously, increasing speed but requiring more hardware resources. Designers must choose between these approaches depending on the system requirements for speed versus resource constraints.
Examples & Analogies
Consider the difference between an individual completing a task alone, one step at a time (bit-serial), versus a team working together to complete the task in much less time (bit-parallel). While the individual may use fewer resources (a single tool), the team will likely need more tools and space but can finish the job faster.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Carry-Lookahead Adders: A technique to reduce delays in addition operations.
-
Wallace Tree Multipliers: A method for speeding up multiplication through parallel processing.
-
Pipelined Architecture: Increases throughput by allowing multiple operations to occur simultaneously.
-
Bit-Serial vs Bit-Parallel: Design choices that balance speed and silicon area.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using a CLA can improve the speed of addition in digital circuits by minimizing carry propagation time.
-
A Wallace Tree multiplier can handle large integer multiplications efficiently, making it ideal for high-performance computing applications.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Carry-Lookahead makes it fast, addition delays are stuck in the past!
π Fascinating Stories
-
Picture a racing event where cars can only travel one at a time versus multiple cars speeding together on a racetrack. The multiple cars represent bit-parallel design, racing to determine who multiplies the fastest!
π§ Other Memory Gems
-
Remember CLAP for the arithmetic speed-ups: Carry-Lookahead for addition, L for Wallace Tree for multiplication, A for Arithmetic Units in Pipelining, and P for Parallel Design trade-offs.
π― Super Acronyms
P.A.C.E. - Pipelining, Addition speed, Carryout anticipation, Efficient design for quick arithmetic logic performance.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: CarryLookahead Adder (CLA)
Definition:
An adder design that reduces carry propagation delays in binary addition.
-
Term: Wallace Tree Multiplier
Definition:
A multiplier design that uses a tree structure to efficiently add partial products in parallel.
-
Term: Pipelining
Definition:
An optimization technique that allows multiple instruction stages to execute simultaneously, increasing throughput.
-
Term: BitSerial Design
Definition:
A design in which data is processed one bit at a time, often requiring less area but taking more time.
-
Term: BitParallel Design
Definition:
A design that processes multiple bits simultaneously, resulting in faster performance but requiring more silicon area.