Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Unsigned Binary Numbers
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to discuss unsigned binary numbers. Can anyone tell me what they think it means to represent numbers in binary?
Does it mean using only 0s and 1s to represent numbers?
Exactly! Unsigned binary numbers specifically represent non-negative integers. Can anyone state the range of these numbers?
Is it from 0 to 2^n - 1, where n is the number of bits?
Well done! This range highlights how the number of bits affects the maximum integer value that can be represented. Let's remember this as '0 to 2^n - 1.' Who can give me an example?
If we have 4 bits, then the range would be from 0 to 15!
Perfect! Remember that with more bits, the range increases as well. We will build on this as we move to signed numbers.
Signed Binary Numbers
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we've covered unsigned numbers, let's dive into signed binary numbers. What are signed numbers used for?
They allow us to represent both positive and negative integers.
Great! We have a few different formats for signed numbers. Who can name one?
I think there's sign-magnitude representation, right?
Correct! In sign-magnitude, the most significant bit is the sign bit. What do you think happens with 1's complement?
You invert all the bits to get the negative version.
Thatβs absolutely right! Lastly, which method is most commonly used and why?
The 2's complement is the most common because it simplifies the arithmetic operations.
Exactly! Keeping all of these formats in mind is important as we learn more about binary arithmetic.
Fixed-Point Representation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Next, let's discuss fixed-point representation. Can anyone explain what fixed-point means?
I believe it has to do with numbers that contain fractional parts but the binary point is fixed at a certain location.
Exactly! Fixed-point is widely used in scenarios where a certain level of precision is required without floating point complexities. Can anyone think of an example of where this could be useful?
Maybe in financial calculations where you need exact values without rounding?
Great example! Remember that fixed-point representation helps maintain precision in applications that cannot tolerate rounding errors.
Floating-Point Representation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Finally, let's talk about floating-point representation. Why do you think it's so important?
It allows us to represent very large and very small numbers efficiently.
Exactly! Floating-point representation, especially using the IEEE 754 standard, provides a structured approach to encoding numbers. Who can remember the components of a floating-point number?
Isn't it the sign bit, exponent, and mantissa?
Right! It breaks numbers down into these components, making it easier for computers to handle them. Can anyone give an example of a floating-point representation?
For 32-bit representation, it would be 1 bit for sign, 8 for exponent, and 23 for mantissa!
Excellent! Understanding floating-point representation is crucial, particularly for scientific and engineering computations.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
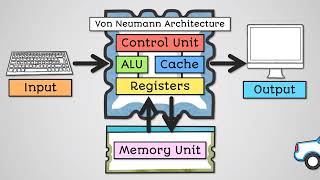
In this section, we explore how numbers are represented in computers, distinguishing between unsigned and signed binary numbers and discussing fixed-point and floating-point representations. Understanding these concepts is crucial for comprehending how arithmetic operations are performed in digital systems.
Detailed
Number Representation in Computers
This section delves into various methods employed in computer systems for representing numbers, which is fundamental to computer arithmetic and system design.
1. Unsigned Binary Numbers
- Definition: Unsigned binary numbers can only represent non-negative integers, meaning they start from zero and go up to a maximum value dictated by the number of bits (n):
Range: \[ 0 \text{ to } 2^n - 1 \].
2. Signed Binary Numbers
- Importance: They are necessary for encoding both positive and negative integers.
- Formats:
- Sign-Magnitude: The most significant bit (MSB) indicates the sign (0 for positive, 1 for negative), and the remaining bits represent the magnitude.
- 1's Complement: Negative numbers are represented by inverting all bits of the corresponding positive number.
- 2's Complement: This method involves inverting all bits and adding 1, being the most commonly used representation because it simplifies arithmetic operations.
3. Fixed-Point Representation
- Usage: Suitable for representing numbers that require fractional parts with a binary point fixed at a certain location.
4. Floating-Point Representation
- Purpose: Enables representation of very large or very small real numbers, accommodating a vast range of values.
- Standard: Follows the IEEE 754 standard to ensure consistency across systems.
- Format: Composed of to a sign bit, an exponent, and a mantissa (Example: For single-precision 32-bit representation: 1 bit for sign, 8 bits for exponent, 23 bits for mantissa).
Understanding these number representation techniques is vital for the design and optimization of arithmetic systems, as they directly affect how arithmetic operations are executed and how software interacts with hardware.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Unsigned Binary Numbers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Represent only non-negative integers.
β Range: 0 to 2βΏ - 1, where n is the number of bits.
Detailed Explanation
Unsigned binary numbers are a way to represent whole numbers without any sign, meaning they can only be zero or positive. The range of values that can be represented using 'n' bits is from 0 up to 2 raised to the power of 'n' minus 1. For example, with 3 bits, the largest unsigned binary number is 111 in binary, which equals 7 in decimal (0 to 7). This method of representation is straightforward and efficient for non-negative number operations.
Examples & Analogies
Think of unsigned binary numbers like a jar that can only hold marbles. Each marble added represents a count. If the jar has three compartments (bits), it can hold a total of seven marbles (0 through 7), but no negative values or empty compartments can represent a count.
Signed Binary Numbers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Format Description
- Sign-Magnitude MSB = sign bit (0 = +, 1 = β); remaining bits = magnitude
- 1βs Complement: Invert all bits to get negative
- 2βs Complement: Invert all bits and add 1 (commonly used)
Detailed Explanation
Signed binary numbers allow for the representation of both positive and negative integers. This is crucial because many real-world applications require the ability to depict both types of values. The representation starts with a sign bit: if it is 0, the number is positive; if it is 1, the number is negative. There are different methods to include the sign in binary representation:
1. Sign-Magnitude: Uses one bit for the sign and the rest for the number's magnitude.
2. 1βs Complement: To find the negative number, you flip all bits of the positive version.
3. 2βs Complement: This is the most common method today because it simplifies binary arithmetic; to find the negative, you flip the bits and add 1 to the least significant bit.
Examples & Analogies
Imagine you are using a weather dial to indicate temperature. The dial can read from -10Β°C to +10Β°C. The topmost pointer (sign bit) indicates direction: if it points left, itβs negative; right, itβs positive. In this case, if we want to show -5Β°C using 1's complement, you would turn the dial to indicate +5Β°C but invert it to reflect the cold. If using 2's complement, youβd turn the dial to +5Β°C and add a degree to adjust to the negative.
Fixed-Point Representation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Used for numbers with fractional parts.
β Binary point is fixed at a specific location.
Detailed Explanation
Fixed-point representation is a method of representing real numbers that contain a fractional part (like 3.75) using a fixed number of bits. Instead of placing the binary point arbitrarily, it is fixed at a specific point. For instance, if you allocate 8 bits, 4 may be for the integer part and 4 for the fractional part. This representation is suitable for applications that require a known and consistent precision but does make it challenging to represent very large or very small numbers.
Examples & Analogies
Consider a digital scale that measures weight in grams. If you isolate the first four marks to represent whole grams and keep the last four marks for decimals, you get a clear understanding of how weight is measured. If the display reads 3.75 kg, it indicates 3 whole kilograms and 750 grams.
Floating-Point Representation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Represents very large or small real numbers.
β Follows IEEE 754 standard.
β Format: Sign bit + Exponent + Mantissa
β Example: 32-bit single precision (1 + 8 + 23)
Detailed Explanation
Floating-point representation is used to represent a vast range of real numbers, both very large and very small. This is achieved by using a format that includes a sign bit (indicating positive or negative), an exponent (which determines how far to 'move' the decimal point), and a mantissa (which contains the significant digits of the number). This method follows the IEEE 754 standard, which outlines how numbers should be represented in a consistent manner across different computing systems. For example, a 32-bit float has 1 bit for the sign, 8 bits for the exponent, and 23 bits for the mantissa.
Examples & Analogies
Think of floating-point representation like scientific notation in mathematics. When representing vast distances in space, itβs more practical to say 1.5 Γ 10^3 km rather than writing 1500 km. Here, the '1.5' stands for significant digits (mantissa), and '3' indicates how many places to move the decimal (exponent).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Unsigned Binary Numbers: Only non-negative integers with a range of 0 to 2^n - 1.
-
Signed Binary Numbers: Represent both positive and negative integers using formats like sign-magnitude and 2's complement.
-
Fixed-Point Representation: Used for representing numbers with fixed binary points allowing for exact fractions.
-
Floating-Point Representation: Represents very large or small numbers using a standard format (IEEE 754).
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An unsigned binary number using 4 bits can represent values from 0 to 15 (0000 to 1111).
-
A signed binary number in 4 bits using 2's complement can represent numbers from -8 to +7.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
In binary we trust, for numbers are a must, unsigned is non-negative, signed can even rust.
π Fascinating Stories
-
Imagine a shopkeeper counting coins (unsigned) vs. a magician balancing positive and negative values (signed) to represent reality.
π§ Other Memory Gems
-
FIXED for Fixed-Point (F-F, I-Integer, X-Fraction, E-Exact, D-Determined) to remember its uses.
π― Super Acronyms
FLOAT for Floating-point (F-Flexible, L-Large range, O-Overflow issues, A-Arithmetic operations, T-Test for precision).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Unsigned Binary Numbers
Definition:
Binary numbers that can only represent non-negative integers.
-
Term: Signed Binary Numbers
Definition:
Binary numbers that can represent both positive and negative integers.
-
Term: SignMagnitude
Definition:
A format for signed numbers where the MSB indicates the sign.
-
Term: 1's Complement
Definition:
A method of representing negative numbers by inverting all bits.
-
Term: 2's Complement
Definition:
A common method for representing negative numbers by inverting all bits and adding 1.
-
Term: FixedPoint Representation
Definition:
A method to represent numbers with fixed binary points allowing for fractions.
-
Term: FloatingPoint Representation
Definition:
A method to represent real numbers that can be very large or small, using a standard format.
-
Term: IEEE 754
Definition:
A technical standard for floating-point arithmetic in computers.