Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Natural Frequencies
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's start by defining natural frequency. What do you think happens when a system, like a building, oscillates at its natural frequency?
I think it would resonate with the building's structural properties, right?
Exactly! Natural frequencies are critical because they signify resonant points where the structure can vibrate harmoniously. Now, can anyone explain why this is vital for structures during an earthquake?
If a building's natural frequency matches the frequency of seismic waves, it could lead to significant vibrations, potentially causing damage.
Right! This alignment of frequencies can amplify oscillations, which is essential for engineers to consider in design.
Exploring Mode Shapes
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's talk about mode shapes. Can someone explain what we mean by a mode shape in the context of structural dynamics?
A mode shape is how a structure deforms when it oscillates at a certain natural frequency.
Exactly! Mode shapes represent independent oscillation patterns, and each shape corresponds to its specific natural frequency. Why do you think this independence matters?
It allows us to analyze complex motions by breaking them down into simpler components, making it easier to predict responses to loads.
Great insight! We can mathematically express these mode shapes as eigenvectors, forming a modal matrix when combined. This brings us to the next point: how do we represent these mathematically?
Mathematical Relationships of Mode Shapes
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s dive into the mathematics. We refer to mode shapes and frequencies as eigenvectors and eigenvalues, respectively. Does anyone remember how we define these mathematically?
Yes! The modal matrix’s columns contain the mode shapes, while the natural frequencies are represented in a diagonal matrix.
Exactly! And what about the orthogonality conditions for these matrices?
The mode shapes are orthogonal with respect to the mass and stiffness matrices, which means they can be used to isolate the motion in analysis.
Absolutely! This property allows us to decouple the equations of motion, making calculations much simpler. Let's summarize the key points before moving on.
Today, we learned about natural frequencies as resonant points of vibration, mode shapes representing unique deformations, and their mathematical representations in modal analysis.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the definitions of natural frequency and mode shape, their physical significance, and mathematical representation. Normal modes are interpreted as independent oscillation patterns, with mode shapes represented as eigenvectors and natural frequencies as eigenvalues, reflecting the inherent properties of vibrational systems.
Detailed
Concept of Mode Shapes and Natural Frequencies
In structural dynamics, particularly in earthquake engineering, normal modes of vibration play a crucial role in analyzing how structures respond to dynamic loads. This section covers the definitions and physical interpretations of two key concepts:
Definitions:
- Natural Frequency: The specific frequency at which a system tends to oscillate in the absence of external forces or damping.
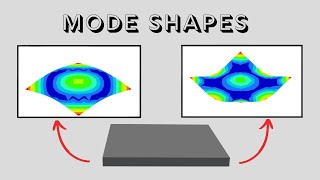
- Mode Shape: The unique deformation shape that corresponds to each natural frequency, characterizing the system's response.
Physical Interpretation:
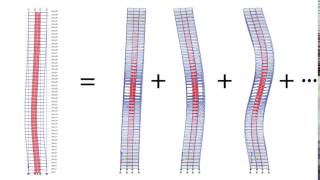
Normal modes can be viewed as independent oscillation patterns of the system. Each mode can oscillate without affecting the others, allowing for a clearer analysis of a complex motion by breaking it down into simpler components.
Mathematical Representation:
Mode shapes and natural frequencies can be expressed mathematically as:
- Eigenvectors: Represent mode shapes, defined in a modal matrix
- Eigenvalues: Correspond to natural frequencies, represented in a diagonal matrix
The mathematical orthogonality conditions are given by:
- Mass Matrix Orthogonality:
- Stiffness Matrix Orthogonality:
This section highlights the importance of these concepts in constructing the underlying theory necessary for the further analysis of multi-degree-of-freedom (MDOF) systems in structural engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Natural Frequency and Mode Shape
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Definition of natural frequency and mode shape
Detailed Explanation
Natural frequency refers to the specific frequency at which a system tends to oscillate when it is disturbed from its rest position and then allowed to move freely. In contrast, a mode shape is the specific pattern of displacement that a system exhibits at that natural frequency. When a structure vibrates, each mode shape represents a different configuration in which the structure can oscillate.
Examples & Analogies
Think of a swing. There is an ideal speed (natural frequency) at which the swing moves most rhythmically; if you push it at that speed, it oscillates back and forth smoothly. The way it moves (mode shape) is the path it takes, which differs if you push it at a different speed.
Physical Interpretation of Normal Modes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Physical interpretation of normal modes: oscillation patterns independent of each other
Detailed Explanation
Normal modes represent distinct ways a structure can vibrate, and each mode is independent of the others. This means if one part of the structure moves in a certain manner, it does not affect how the other parts move in their respective modes. This independence is crucial for understanding vibration behaviors in complex structures.
Examples & Analogies
Imagine a group of dancers performing different styles of dance at the same time—some may be doing ballet while others are breakdancing. Each dancer moves independently according to their style (normal mode), creating a composite performance without interfering with each other's routines.
Mode Shapes as Eigenvectors and Natural Frequencies as Eigenvalues
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Mode shapes as eigenvectors and natural frequencies as eigenvalues
Detailed Explanation
In mathematical terms, mode shapes can be represented as eigenvectors of a system, while the corresponding natural frequencies can be seen as eigenvalues. This mathematical relationship allows for the analysis of structures through linear algebra, simplifying the process of determining how they will behave under dynamic loads.
Examples & Analogies
Consider a classroom where each student represents a mode shape (eigenvector) and the scores they receive on a test represent the natural frequencies (eigenvalues). Just as each student has a unique score and style of learning (mode shape), each vibration mode has its own characteristics.
Orthogonality of Mode Shapes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Orthogonality of mode shapes with respect to mass and stiffness matrices
[Φ]T[M][Φ]=[I], [Φ]T[K][Φ]=[Λ]
where:
– [Φ] = modal matrix (mode shapes as columns)
– [Λ] = diagonal matrix of squared natural frequencies
– [I] = identity matrix
Detailed Explanation
Orthogonality of mode shapes means that modes do not influence one another. In mathematical terms, this is expressed via relationships involving mass [M] and stiffness [K] matrices. When the mode shapes are orthogonal, it simplifies the calculations of dynamic responses since they can be analyzed independently. The identity matrix [I] suggests that there is no overlap among the modes.
Examples & Analogies
Think of different musical instruments in a band playing at the same time. Each instrument produces its unique sound (mode). When played together, their sounds complement each other without interfering, allowing for a harmonious performance. This is similar to orthogonal modes that sustain their unique characteristics while contributing to the overall response.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Natural Frequencies: Frequencies at which structures tend to oscillate without external forces.
-
Mode Shapes: Unique deformation patterns associated with respective natural frequencies.
-
Eigenvectors and Eigenvalues: Mathematical representations for mode shapes and natural frequencies.
-
Orthogonality: The principle that different mode shapes are independent and can be analyzed separately.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A building swaying during an earthquake experiences natural frequencies that align with seismic waves, potentially leading to resonance and amplified movements.
-
In a guitar string, the fundamental mode shape represents its first vibration pattern, producing the lowest pitch of sound.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When structures sway like trees in the breeze, at their natural frequency, their movement is a tease.
📖 Fascinating Stories
-
Imagine a playground swing that only swings high when pushed just right. Each push is like a force acting on our building. If pushed at just the right frequency, it sways perfectly high, just like how buildings sway during earthquakes.
🧠 Other Memory Gems
-
To remember eigenvalues and eigenvectors, think: 'E-V, Everything Vibrates.' E for eigenvalues (natural frequencies), V for eigenvectors (mode shapes), helping us recall their connection.
🎯 Super Acronyms
M.O.E. - Mode Shapes, Orthogonality, Eigenvalues
- Remember these fundamentals to understand vibrations and structural behavior.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Natural Frequency
Definition:
The frequency at which a system naturally oscillates when not subjected to external forces.
-
Term: Mode Shape
Definition:
The specific shape or deformation of a structure corresponding to a natural frequency during oscillation.
-
Term: Eigenvector
Definition:
A non-zero vector that changes only in scale during a linear transformation, representing mode shapes in structural dynamics.
-
Term: Eigenvalue
Definition:
A scalar value associated with an eigenvector, representing natural frequencies in structural dynamics.
-
Term: Orthogonality
Definition:
A property indicating that two vectors (or mode shapes) are perpendicular to each other with respect to a specified inner product.