Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Assumptions in Free Vibration Analysis
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will begin by discussing some fundamental assumptions in our analysis of free vibrations in MDOF systems. Can anyone tell me what we assume about external forces?
I think we assume there are no external forces acting on the system.
Correct! We also assume that there is no damping in the system. This simplifies our equations significantly. Why do you think this is important?
Because it lets us focus on the natural vibrations of the system without interference.
Exactly. By focusing on undamped systems, we make it easier to analyze the natural frequencies and mode shapes.
Harmonic Motion in MDOF Systems
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Next, let’s talk about harmonic motion, which we use as a solution form. What does the harmonic motion solution look like?
It’s written as {X(t)}={ϕ}sin(ωt), right?
Yes! {ϕ} represents the mode shape, and ω is the natural frequency. Can anyone explain why we express it this way?
I guess it helps to see how the system oscillates over time!
Spot on! Now, when we substitute this into our equations of motion, we derive a significant characteristic equation. Who can tell me what that is?
Isn’t that the one involving the mass and stiffness matrices?
Yes! It gives us ([K]−ω²[M]){ϕ}=0. This is crucial for finding our natural frequencies.
Eigenvalue Problem in MDOF Systems
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we have our eigenvalue problem, what’s the next step we would take to find our natural frequencies?
We need to solve the characteristic equation, det([K]−ω²[M])=0.
Correct! What does solving this equation give us?
It gives us the natural frequencies and the corresponding mode shapes, right?
Exactly. Understanding these dynamics is crucial for predicting how architectures will respond in real-world situations, especially under vibrations like those caused by earthquakes.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section delves into the free vibration analysis of MDOF systems by assuming no damping and no external forces. It introduces harmonic motion solutions and formulates the eigenvalue problem to extract natural frequencies and mode shapes, showcasing the procedures required to derive these essential insights into structural dynamics.
Detailed
Free Vibration Analysis of MDOF Systems
In this section, we explore the fundamentals of free vibration analysis specifically for multi-degree-of-freedom (MDOF) systems. We begin with some key assumptions: we consider scenarios where there is no damping present in the system, and no external forces are acting on it.
Key Concepts and Process:
The solution for free vibrations involves assuming a harmonic motion model, expressed mathematically as {
X(t)}={ϕ}sin(ωt). This representation insists on substituting the assumed solution back into the system's equations of motion. When doing so, we arrive at the eigenvalue problem defined by the equation ([K]−ω²[M]){ϕ}=0.
Steps to Solve the Free Vibration Problem:
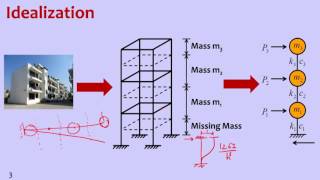
- Formulate the Mass and Stiffness Matrices: Identify and set up the mass and stiffness matrices pertinent to the MDOF system being analyzed.
- Solve the Characteristic Equation: Apply the determinant operation on the resultant equation to derive the characteristic equation, det([K]−ω²[M])=0. This is crucial for identifying the natural frequencies of the system.
- Obtain Natural Frequencies and Mode Shapes: The solutions to the characteristic equation yield the natural frequencies (ω) and their corresponding mode shapes (ϕ), which define how the system will vibrate naturally.
The section highlights the importance of determining these characteristics, as they provide critical insights into the dynamic behavior of structures when subjected to vibrational forces. Such understanding is vital for the design and evaluation of structures in earthquake engineering and structural dynamics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Assumptions for Free Vibration Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Assumption of no damping and no external force.
Detailed Explanation
In free vibration analysis, one of the key assumptions is that there is no damping in the system and that no external forces are acting on it. This simplifies the analysis because damping typically dissipates energy, making it more complex to analyze the system's response. By assuming no external forces, we isolate the natural oscillatory behavior of the system, focusing solely on its inherent characteristics.
Examples & Analogies
Imagine a swing in a park. If you push the swing (an external force) or if the swing has some friction (damping), it doesn't oscillate in a simple manner. However, if you let the swing go without pushing it or if it were perfectly smooth (no friction), it would swing back and forth in a predictable, regular pattern. This is similar to the concept of free vibration in engineering.
Solution Approach using Harmonic Motion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Solution using harmonic motion: {X(t)} = {ϕ}sin(ωt)
Detailed Explanation
To solve the free vibration problem of MDOF systems, we assume that the motion of the system can be described using harmonic functions, specifically sinusoidal functions. Here, {X(t)} represents the displacement of the system as a function of time, {ϕ} stands for the mode shape of the system, and ω denotes the angular frequency of the oscillation. This approach allows us to express the complex motion of the system in terms of simpler oscillatory modes, which are easier to analyze.
Examples & Analogies
Think of tuning forks. Each fork vibrates at a specific frequency, producing a clear tone when struck. If you represent how the fork vibrates over time, that motion can be described using sinusoidal functions. Similarly, by expressing a complex vibrating system into its fundamental modes of motion using harmonic functions, engineers can better understand and predict the system's behavior.
Formulating Eigenvalue Problem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Substituting into equations of motion leads to: ([K]−ω²[M]){ϕ} = 0
Detailed Explanation
When we substitute the harmonic motion solution into the equations of motion for the MDOF system, we arrive at the expression ([K]−ω²[M]){ϕ} = 0. This forms an eigenvalue problem, where the goal is to find the values of ω² (which represent squared natural frequencies) and the corresponding mode shapes {ϕ}. This is a critical step because solving this eigenvalue problem yields the natural frequencies at which the system tends to oscillate freely.
Examples & Analogies
Imagine a set of swings in a playground. Each swing can be set into motion at specific frequencies based on its length and weight. The frequencies at which these swings resonate are akin to the natural frequencies we find in the mathematical model. By determining those frequencies (eigenvalues), we can understand how the swings (mode shapes) will behave when set in motion.
Procedure for Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Procedure:
a. Formulate [M] and [K]
b. Solve characteristic equation det([K]−ω²[M])=0
c. Obtain natural frequencies ω and corresponding mode shapes {ϕ}**
Detailed Explanation
The analysis of free vibrations of MDOF systems can be systematically approached through the following steps:
1. First, we need to define the mass matrix [M] and stiffness matrix [K] that characterize the system's properties.
2. Next, we solve the characteristic equation, which involves finding the determinant of the matrix ([K]−ω²[M]) and setting it equal to zero. This step indicates the values of ω for which the system can oscillate.
3. Finally, using these natural frequencies, we can determine the associated mode shapes. This provides us with a complete picture of how the system will behave in free vibration.
Examples & Analogies
Think of building a musical instrument, like a guitar. First, you determine the materials and dimensions (analogous to formulating [M] and [K]). Then, you figure out the notes it plays as you pluck it (analogous to solving the characteristic equation for natural frequencies). Lastly, you visualize or hear the specific sounds each note makes (determining mode shapes). Following these steps leads you to understand the complete sound profile of the guitar.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
The solution for free vibrations involves assuming a harmonic motion model, expressed mathematically as {
-
X(t)}={ϕ}sin(ωt). This representation insists on substituting the assumed solution back into the system's equations of motion. When doing so, we arrive at the eigenvalue problem defined by the equation ([K]−ω²[M]){ϕ}=0.
-
Steps to Solve the Free Vibration Problem:
-
Formulate the Mass and Stiffness Matrices: Identify and set up the mass and stiffness matrices pertinent to the MDOF system being analyzed.
-
Solve the Characteristic Equation: Apply the determinant operation on the resultant equation to derive the characteristic equation, det([K]−ω²[M])=0. This is crucial for identifying the natural frequencies of the system.
-
Obtain Natural Frequencies and Mode Shapes: The solutions to the characteristic equation yield the natural frequencies (ω) and their corresponding mode shapes (ϕ), which define how the system will vibrate naturally.
-
The section highlights the importance of determining these characteristics, as they provide critical insights into the dynamic behavior of structures when subjected to vibrational forces. Such understanding is vital for the design and evaluation of structures in earthquake engineering and structural dynamics.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A multi-storey building swaying during an earthquake exhibits free vibration characteristics.
-
A vehicle hitting a pothole causes oscillations that can be analyzed as free vibrations.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
No forces in sight, no dampening might, helps frequencies take flight!
📖 Fascinating Stories
-
Imagine a swing, perfectly still until someone gives it a push. This can represent natural frequencies as the swing moves. If nobody pushes, it sways freely without external forces.
🧠 Other Memory Gems
-
FINE - Free, Inertia, No external forces, Eigenvalue problem.
🎯 Super Acronyms
SINE for the solution—Solution, Initial, Natural frequency, Eigenvalues.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Free Vibration
Definition:
Oscillation of a system without external forces or damping.
-
Term: Natural Frequency
Definition:
Frequency at which a system tends to oscillate in free vibration.
-
Term: Mode Shape
Definition:
The specific deformation pattern associated with a natural frequency.
-
Term: MDOF Systems
Definition:
Multi-Degree-of-Freedom systems with multiple independent coordinates.
-
Term: Eigenvalue Problem
Definition:
Mathematical formulation that defines the relationship between a square matrix and its eigenvalues/vectors.