Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Damping Effects
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we are going to examine the effect of damping on mode shapes. First, can anyone tell me what they think damping is in the context of vibration?
I think damping refers to how vibrations decrease over time.
That's correct! Damping is indeed the process that reduces the amplitude of vibrations. In undamped systems, modes are simply real and orthogonal. Can someone tell me what orthogonality means in this context?
Doesn't it mean that the modes don’t interfere with each other and are independent?
Exactly! Each mode vibrates independently. However, once we introduce damping, the situation changes. What do you think happens to the mode shapes in a damped system?
I believe they might become coupled?
Yes, in damped systems, especially if the damping is non-proportional, the modes may couple and produce complex mode shapes. Let's summarize: Damping affects the realness and orthogonality of modes.
Types of Damping
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's dive into the types of damping. We have classical or proportional damping. Who can describe this type?
Classical damping is when the damping matrix is proportional to the mass and stiffness matrices.
Well said! And what about non-classical damping?
Isn't that when the damping doesn't follow that ratio, leading to complex eigenvalues?
Exactly! Non-classical damping results in more complex dynamics. So, what kind of challenges might this present in analysis?
It could make it harder to predict the behavior of the structure under load.
That's right! Non-classical damping complicates our predictions. It’s crucial to understand these types when designing for seismic loads.
Understanding Modal Damping Ratios
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let’s focus on modal damping ratios. Can anyone tell me how they are defined?
They’re defined for each mode, based on its mass and stiffness.
Correct! The ratio indicates whether a mode is underdamped, critically damped, or overdamped. Who can explain what each of these terms means?
Underdamped means the system oscillates but eventually settles down, critically damped is where it returns to equilibrium as quickly as possible without oscillating, and overdamped means it returns slowly without oscillating.
Great job! The modal damping ratio provides insights into how different modes will respond under different conditions, which is critical for design in seismic engineering. Remember the acronym UCO for underdamped, critically damped, and overdamped to help you recall these definitions!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Damping significantly alters the characteristics of vibrational modes in a system. Undamped systems exhibit real and orthogonal mode shapes, while damped systems can show complex eigenvalues and coupled mode shapes, especially under non-proportional damping. The section also introduces modal damping ratios to categorize the behavior of damped systems.
Detailed
In this section, we explore the effect of damping on mode shapes in vibrating systems, especially in the context of earthquake engineering. Undamped systems possess purely real and orthogonal modes, which means the normal modes oscillate independently of each other. However, when damping is introduced, especially non-proportional damping, the modes may couple, leading to complex eigenvalues and non-orthogonal mode shapes. The section categorizes damping into classical (proportional) and non-classical (non-proportional) damping and emphasizes how classical damping maintains uncoupled modal equations. The concept of modal damping ratios is introduced, where each mode is assigned a damping ratio (ζ), indicating whether it is underdamped, critically damped, or overdamped. This categorization is essential for analyzing the system's response under various loading conditions.
Youtube Videos
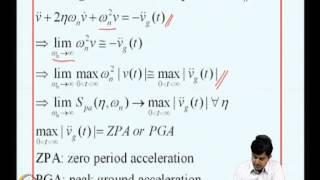
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Damped vs. Undamped Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Damped Systems vs. Undamped Systems:
- In undamped systems, mode shapes are purely real and orthogonal.
- In damped systems, damping may couple the modes, especially if damping is non-proportional.
Detailed Explanation
In this section, we explore the differences between damped and undamped systems. An undamped system is one where there are no energy losses, meaning it vibrates freely. In such systems, the mode shapes (the patterns of motion) are clear, predictable, and never overlap (orthogonal). However, in damped systems (where energy is lost, for example through friction), the behavior changes. Damping can mix these modes, making them less distinct and more coupled, especially when the damping isn't proportional—that is, it doesn't behave uniformly across different modes.
Examples & Analogies
Imagine you have a perfectly smooth surface for a ball to roll on (an undamped system), the ball rolls in a straightforward path without deviation. Now, consider a bumpy surface (a damped system) where the ball not only rolls but also bounces and changes its path due to the bumps. The bumps (damping) mix movements that were once separate and straightforward.
Types of Damping
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Types of Damping:
- Classical (Proportional) Damping:
[C]=α[M]+β[K]
• Leads to uncoupled modal equations.
- Non-Classical (Non-Proportional) Damping: Leads to complex modes and complex eigenvalues.
Detailed Explanation
This chunk defines two categories of damping: classical and non-classical. Classical (or proportional) damping refers to a system where the damping matrix can be expressed as a combination of the mass and stiffness matrices. This type of damping allows for simpler calculations where each mode can still behave independently, leading to clear modal equations. In contrast, non-classical damping causes the modes to couple in complex ways, resulting in more intricate relationships represented by complex modes and eigenvalues, making solutions more complicated.
Examples & Analogies
Think of classical damping like a well-tuned orchestra where each instrument plays its part clearly, maintaining its own rhythm. Non-classical damping, on the other hand, is like a jazz band where instruments can sometimes blend into one another, creating a more chaotic sound. In order to understand the music (the motion of the system), you need to listen closely to discern the different parts.
Modal Damping Ratios
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Modal Damping Ratios:
- Defined for each mode:
c
ζ = √ n
n
2 k m
n n
• ζ <1: Underdamped
• ζ =1: Critically damped
• ζ >1: Overdamped
Detailed Explanation
Modal damping ratios help quantify how different modes behave in response to damping. They are defined for each mode and calculated using the properties of the system. If the damping ratio (ζ) is less than 1, the system is underdamped, meaning it oscillates but gradually decreases in amplitude over time. If ζ equals 1, the system is critically damped, which means it returns to its equilibrium position as quickly as possible without oscillating. If ζ is greater than 1, the system is overdamped, returning to equilibrium slowly without any oscillations. These ratios help engineers understand how the system will react under various conditions.
Examples & Analogies
Think of a swing at a park. If someone pushes it gently (underdamped), it swings back and forth slowly losing its energy over time. If you give it just the right push to stop it at the highest point without swinging back (critically damped), it will come to a stop quickly. If you hold it firmly without letting it swing (overdamped), it barely moves back and forth and just settles slowly at the rest position.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Damping: The process of reducing oscillation amplitude in a system.
-
Orthogonality: Independence of oscillation modes in a system.
-
Classical Damping: Proportional response in damping allowing for uncoupled equations.
-
Non-Classical Damping: Leads to coupled modes and complex eigenvalues.
-
Modal Damping Ratios: Indicators of the strength of damping in modes.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In civil engineering, classical damping is often used for designs intended to meet seismic performance criteria.
-
In automotive engineering, non-classical damping can influence vehicle dynamics and comfort by altering how vibrations are managed.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Damping reduces the sway, keeping oscillations at bay.
📖 Fascinating Stories
-
Imagine a pendulum swinging—without anything to slow it down, it would move forever. But if you use a damping fluid, it settles down smoothly and doesn't swing back and forth indefinitely.
🧠 Other Memory Gems
-
Remember the acronym 'UCO' for understanding damping ratios: U for underdamped, C for critically damped, and O for overdamped.
🎯 Super Acronyms
Use 'DAMP' to recall
- Damping Amplitude Modulates Performance!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Damping
Definition:
A process that reduces the amplitude of oscillations over time.
-
Term: Orthogonality
Definition:
A property indicating that two modes do not interfere with each other.
-
Term: Classical Damping
Definition:
Damping proportional to mass and stiffness matrices, leading to uncoupled modal equations.
-
Term: NonClassical Damping
Definition:
Damping that does not follow the proportionality relationship, leading to complex modes.
-
Term: Modal Damping Ratio (ζ)
Definition:
A ratio indicating the level of damping in a mode, with classifications: underdamped (ζ < 1), critically damped (ζ = 1), and overdamped (ζ > 1).