Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Modal Analysis
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're diving into the Modal Analysis Technique. Why do you think decoupling equations might be beneficial?
It helps simplify complex problems, making them easier to solve.
Exactly! When we deal with multi-degree-of-freedom systems, which are common in structures, we have these coupled differential equations that can be quite complicated. The goal here is to transform those into simpler forms.
What do you mean by transforming them?
Good question! We introduce modal coordinates, where we express our displacement vector in terms of a modal matrix that represents the mode shapes of the system.
Defining Modal Coordinates
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
So, we define modal coordinates using the equation {X} = [Φ]{q}. Can anyone tell me what {q} represents?
It's the modal coordinate vector, right?
Correct! By substituting this into our original equations of motion, we end up with this form: [M][Φ]{q¨} + [K][Φ]{q} = {F(t)}. Notice how we essentially factor out the complexities.
So, does that mean we can solve each equation independently now?
Yes! That’s the beauty of this technique. Each modal equation can be treated as a single-degree-of-freedom equation, which is much simpler to solve.
Solving Independent Equations
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Once we have our uncoupled equations of the form q¨ + ω²q = F(t), we can solve them separately. Why do you think this is advantageous?
It allows us to easily model each mode's response to external forces.
Exactly! And after obtaining the responses for each {q_n}, the total response of the system will be {X(t)} = Σ {ϕ_n} q_n(t). This highlights how we combine the individual modal responses.
So we can visualize the overall behavior of complex structures just by looking at these simpler component modes?
That's right, well summarized! Always remember the principle of superposition in this context.
Applications in Engineering
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's connect this to real-world applications. How is modal analysis significant in earthquake engineering?
It helps in predicting how buildings will respond during earthquakes.
Right! By understanding the modal properties, engineers can design buildings that withstand seismic forces better.
Does this influence where reinforcements are placed in structures?
Absolutely! The mode shapes inform effective structural reinforcements and ensure overall safety.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the modal analysis technique is introduced as a method to simplify the equations governing multi-degree-of-freedom (MDOF) systems. By defining modal coordinates, it transforms the original coupled equations into a set of uncoupled single-degree-of-freedom equations, which can each be solved independently for their responses under external forces.
Detailed
The Modal Analysis Technique aims to simplify the analysis of structures subjected to dynamic loading by decoupling complex systems of equations into manageable parts. This technique involves defining modal coordinates through a transformation, where the original displacements are expressed in terms of mode shapes. By substituting these modal coordinates back into the equations of motion, the system is reduced to a set of independent single-degree-of-freedom (SDOF) equations. These uncoupled equations can be solved individually, making it easier to understand the structural response. This analysis is critical in fields like civil engineering, where accurate predictions of vibrational behaviors are necessary for design and safety. The resulting total response can be reconstructed by summing the individual modal responses, emphasizing the completeness of the analysis across the structural response metrics.
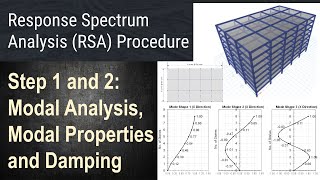
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Objective of Modal Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Objective: To decouple coupled differential equations using modal transformation
Detailed Explanation
The primary goal of modal analysis is to simplify complex systems of equations, which can become very challenging to solve. By using modal transformation, we convert complicated coupled differential equations into simpler, uncoupled ones that are easier to handle. This process allows engineers to analyze vibrational systems more effectively.
Examples & Analogies
Think of modal analysis like translating a complicated recipe with many ingredients and steps into a simpler version that clearly outlines the main idea and ingredients. By focusing only on the main components, you can easily follow the recipe without getting lost in the details.
Defining Modal Coordinates
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Define modal coordinates:
{X}=[Φ]{q}
• where {q} = modal coordinate vector
Detailed Explanation
In this step, we define what are known as modal coordinates. The equation describes the relationship between the physical displacement of a system, {X}, and its modal coordinates, {q}. Here, [Φ] is referred to as the modal matrix that consists of the mode shapes. The {q} is a vector that represents how the system moves in these modal shapes. This transformation helps us to express the system's behavior in a more manageable form.
Examples & Analogies
Imagine a puppet theater where the puppets represent different mode shapes. The modal coordinates can be thought of as the strings controlled by the puppeteer. By manipulating these strings (modal coordinates), you can make the puppets (physical displacements) move in specific ways without altering the puppets themselves.
Substituting into the Original Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Substituting into the original equation:
[M][Φ]{q¨}+[K][Φ]{q}={F(t)}
Detailed Explanation
This equation represents the application of modal coordinates in the original system's equations of motion. Here, [M] is the mass matrix and [K] is the stiffness matrix. By substituting the defined modal coordinates into the original equations, we can derive new equations that correspond to each mode. This simplification plays a crucial role in solving the equations step by step.
Examples & Analogies
Think of this substitution like switching from general driving instructions to specific GPS directions. Just as GPS simplifies the navigation route into clear directions for each turn, substituting modal coordinates converts the complex motion into clearer equations that can be dealt with one at a time.
Using Orthogonality Properties
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Using orthogonality properties:
{q¨}+[Λ]{q}=[Φ]T{F(t)}
Detailed Explanation
In this equation, the orthogonality properties of mode shapes allow us to separate the equations into independent motions. This means that the movement described by each mode does not influence the other motions. The diagonal matrix [Λ] contains the square of the natural frequencies, which are key parts of the uncoupled equations, helping to solve them one by one.
Examples & Analogies
Consider a string quartet playing music where each musician plays a separate melody. The harmony they create is beautiful, but each musician’s play (mode) does not interfere with the others. This example illustrates how each mode operates independently while contributing to the overall response.
Resulting Simplified Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Result: A set of uncoupled single-degree-of-freedom (SDOF) equations
• Each equation can be solved independently:
q¨ +ω2q =F (t)
n n n n
Detailed Explanation
The outcome of the modal analysis transformation is a series of uncoupled single-degree-of-freedom (SDOF) equations. These SDOF equations represent the independent behavior of each mode. Instead of one complicated equation to solve, we now have several simple equations that can be tackled one at a time. This greatly facilitates the process of finding solutions or responses.
Examples & Analogies
Think of solving a series of simple math problems instead of one big, complicated problem. It’s easier to add multiple sums together (like solving each mode) than to try to solve everything at once. This modular approach reduces potential errors and clarifies the path to the solution.
Total Response of the System
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• The total response:
N
X
{X(t)}= {ϕ }q (t)
n n
n=1
Detailed Explanation
The total response of the system, represented as {X(t)}, is achieved by summing all the contributions from each individual mode. Each mode shape {ϕ } corresponds to its respective modal coordinate q(t). This overall response captures the complete behavior of the structure under dynamic loads, allowing engineers to understand and predict how the structure will respond to various forces.
Examples & Analogies
Consider a team effort where each team member contributes to a project. Each person (mode) works on their portion, and when you bring all their work together, you get the final product (total response). This collaborative effort ensures that all aspects are covered, providing a more comprehensive overview.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Modal Analysis Technique: A method to decouple multiple equations in dynamic analysis.
-
Modal Coordinates: A representation of the system's behavior in an uncoupled form.
-
Natural Frequencies: Frequencies at which a system naturally vibrates without external forces.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a two-degree-of-freedom system, modal analysis can simplify the understanding of how the system oscillates in response to dynamic loads.
-
Analyzing a multi-storey building's vibration modes helps to determine how different floors contribute to overall structural response during an earthquake.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To learn about modes and how they sway, modal analysis is the best way!
📖 Fascinating Stories
-
Imagine a conductor directing each musician in an orchestra. Each musician plays their part independently, leading to a beautiful symphony, analogous to how modal analysis allows each mode to contribute to the system’s response without interfering with each other.
🧠 Other Memory Gems
-
DC - Decouple and Combine: Remember to Decouple equations and then Combine individual modal responses for total system analysis.
🎯 Super Acronyms
MODE - Modal Operations Decouple Equations
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Modal Coordinates
Definition:
A transformation of the displacement vector into terms that represent modal shapes for analysis.
-
Term: Eigenvalue Problem
Definition:
A mathematical problem where we seek magnitudes (natural frequencies) that exhibit specific behaviors in a system.
-
Term: SingleDegreeofFreedom (SDOF)
Definition:
A simplified model representing a system with only one degree of freedom, typically easier to analyze.