Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to MDOF Systems
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we're discussing Multi-Degree-of-Freedom or MDOF systems. Can anyone tell me what that means?
Does it mean systems that can move in multiple ways?
Exactly! MDOF systems can oscillate in various patterns. For example, think of a tall building swaying during an earthquake—it's not just moving back and forth; it can twist, lean, and more.
What kind of examples do we have for MDOF systems?
Good question! Common examples include bridges and high-rise buildings. These structures respond dynamically and exhibit very complex motions.
So, can you show us how we model these systems mathematically?
Of course! In MDOF systems, we use equations like this: [M]{X''} + [K]{X} = {F(t)}. Here, [M] is the mass matrix that considers the weight of the structure, while [K] is the stiffness matrix that determines how much it resists deformation. Remember 'M' for mass and 'K' for stiffness!
What does {X} represent?
Great inquiry! {X} refers to the displacement vector, which indicates how much each part of the structure moves. Let's summarize—MDOF systems show how structures respond to dynamic loads with multiple oscillation patterns, requiring proper mathematical modeling.
Equations of Motion in MDOF Systems
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let’s look at the equations of motion in MDOF systems. Why do we express them in matrix form?
Maybe because it helps in simplifying complex systems?
Exactly! Using matrix form allows us to manage the relationships between different degrees of freedom efficiently. It also helps in solving the coupled differential equations.
So why are they called coupled equations?
Great query! They're called coupled because the motion of one degree of freedom affects the others due to their interactions. This interdependence complicates the direct solving process.
How do we solve these equations then?
Typically, we employ numerical methods, like finite element analysis or software tools, to approximate the solutions for these equations. Remember, due to their complexity, solving MDOF systems analytically can be quite challenging!
What are some practical implications of solving these equations?
By correctly solving these equations, we can predict how structures will behave under loads such as earthquakes, allowing for effective design and safety measures. To encapsulate, MDOF modeling involves understanding mass and stiffness matrices to address dynamic responses effectively.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
MDOF systems are essential in understanding structural dynamics, as they allow for the analysis of complex vibrations experienced by structures. The mathematical modeling of these systems is vital, involving coupled differential equations and matrix representations of mass and stiffness.
Detailed
Detailed Summary
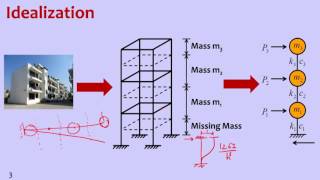
Multi-Degree-of-Freedom (MDOF) Systems represent structural frameworks, such as multi-storey frames, which are capable of exhibiting complex vibrational motions when subjected to dynamic forces like seismic activity. This section defines MDOF systems and emphasizes the importance of mathematical modeling in analyzing such frameworks. The equations of motion are expressed in matrix form as:
$$[M] {X}'' + [K] {X} = {F(t)}$$
- where [M] is the mass matrix, [K] is the stiffness matrix, {X} denotes the displacement vector, and {F(t)} signifies the external force vector.
Furthermore, the uncoupled nature of normal modes makes solving these systems challenging, as the equations become coupled differential equations, hindering straightforward solutions. Understanding MDOF systems, their representation, and underlying concepts is crucial for effectively analyzing structural reactions in real-world conditions.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition and Examples of MDOF Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Definition and examples of MDOF systems
Detailed Explanation
Multi-Degree-of-Freedom (MDOF) systems refer to structures that have multiple ways in which they can move or deform under loads. Unlike Single-Degree-of-Freedom (SDOF) systems, which can be simplified to a single motion, MDOF systems have many interconnected elements that can move in different directions. Examples of MDOF systems include multi-storey buildings, bridges, and large towers, where each floor of the building can sway independently during events like earthquakes.
Examples & Analogies
Imagine a playground swing set with multiple swings. Each swing can move back and forth independently, similar to how each part of a multi-storey building can sway differently during an earthquake. Just like each swing’s motion can be influenced by the others, the behavior of a building or bridge during a seismic event is affected by its various components working together.
Mathematical Modeling of MDOF Structures
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Mathematical modeling of MDOF structures (e.g., multi-storey frames)
Detailed Explanation
To analyze MDOF systems mathematically, we create models that describe how the system behaves under external forces. For example, in a multi-storey building model, we consider each floor as an individual mass connected by beams and columns that provide stiffness. By setting up a mathematical representation, we can solve for movements, forces, and stresses in the building structure.
Examples & Analogies
Think of a large toy building made of blocks. Each block represents a floor, and the connections between them represent the beams and columns. When you push down on the top block, it influences the blocks below it based on how well they’re connected—this is similar to how real buildings respond to forces like wind or earthquakes through mathematical models.
Equations of Motion in Matrix Form
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Equations of motion in matrix form:
[M]{X¨}+[K]{X}={F(t)}
• where:
– [M] = mass matrix
– [K] = stiffness matrix
– {X} = displacement vector
– {F(t)} = external force vector
Detailed Explanation
The behavior of MDOF systems is typically described using matrices. The equation of motion combines the mass matrix [M], which represents how mass is distributed, the stiffness matrix [K], which shows how stiff the structure is, and the external force vector {F(t)}, which accounts for forces applied to the system. The displacement vector {X} represents how far each part of the structure moves. This representation allows engineers to apply advanced mathematical techniques to solve for the movement of the entire structure under different load conditions.
Examples & Analogies
Imagine a large orchestra where different musicians play different instruments. Each musician (mass) plays a unique melody (displacement), and when a conductor (external force) directs them, their sound (response of the system) needs to be well coordinated to create harmonious music (solution). Similarly, the matrices [M] and [K] help engineers see how the entire structure moves together when exposed to forces.
Coupled Differential Equations and Challenges
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Coupled differential equations and challenges in solving them directly
Detailed Explanation
MDOF systems can be mathematically complex because they often result in coupled differential equations. This means that the motion of one part of the system is dependent on the motion of another part, making direct solutions difficult. Solving these equations typically requires numerical methods or advanced mathematical techniques, and the interdependence of different parts can lead to challenges in understanding the overall system behavior.
Examples & Analogies
Think of a team of rowers in a boat. If one rower slows down or changes their rhythm, others must adjust their strokes to maintain balance and speed. This interdependence in a rower's movements mimics the coupled behavior in MDOF systems. Just like adjusting one rower's position affects the entire boat, solving one part of a coupled differential equation affects the solution for the whole MDOF system.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
MDOF Systems: Systems with multiple oscillation capabilities.
-
Mass Matrix: A representation of mass distribution in the system.
-
Stiffness Matrix: The synthesis of resistance to deformation in a structure.
-
Coupled Differential Equations: Equations that cannot be decoupled easily due to interactions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A multi-storey building during an earthquake showcasing complex oscillations.
-
A bridge swaying in response to traffic and environmental forces, exemplifying MDOF dynamics.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
MDOF structures sway and bend, in complex ways they do extend.
📖 Fascinating Stories
-
Imagine a tall tower dancing in the wind; each floor has its own rhythm, moving in sync yet wildly different!
🧠 Other Memory Gems
-
To remember the parts of the equation [M]{X}'' + [K]{X} = {F(t)}, think 'Mass, Motion, Kinetics to Forces'.
🎯 Super Acronyms
MDOF
- Multiple Directions of Oscillation Functionality.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: MultiDegreeofFreedom (MDOF) Systems
Definition:
Systems with multiple degrees of freedom allowing complex motion under dynamic loads.
-
Term: Mass Matrix
Definition:
A matrix that represents the distribution of mass in a dynamic system.
-
Term: Stiffness Matrix
Definition:
A matrix that describes the stiffness characteristics of the system.
-
Term: Displacement Vector
Definition:
A vector that describes the movement of each degree of freedom in a dynamic system.
-
Term: Coupled Differential Equations
Definition:
Equations representing interdependent dynamic equations within a system.
-
Term: Matrix Form
Definition:
A representation of physical quantities in matrix notation to simplify calculations.
-
Term: Dynamic Loads
Definition:
Forces that vary with time, such as wind or earthquake forces.