Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Equation of Motion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will explore the equation of motion for a Single Degree of Freedom system under seismic loading. The equation is mx¨(t) + cx˙(t) + kx(t) = −mu¨g(t). Does anyone know what each of these variables represents?
I think m is the mass of the structure, right?
Correct, Student_1! Here, 'm' stands for mass. 'c' is the damping coefficient, and 'k' is the stiffness of the structure. Why do you think these parameters are important during an earthquake?
Because they determine how much the building moves?
Exactly! The response depends on mass, stiffness, and damping. And what is 'u¨g(t)'?
'u¨g(t)' represents the ground acceleration, which is the external force acting on the building.
Great job! Understanding this is crucial for predicting structural responses during earthquakes.
Types of Structural Response
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s discuss the different types of structural responses to dynamic loads. We have elastic, inelastic, and resonance responses. What do you think happens in an elastic response?
In an elastic response, the building goes back to its original shape after the load is removed.
Right! Now, what about inelastic response?
Inelastic response means there is some permanent deformation?
Exactly again! Now, can someone explain what resonance is?
Resonance occurs when the frequency of the ground motion matches the natural frequency of the structure, amplifying its response.
Perfect! Remember: Elastic means recovery, inelastic means some damage, and resonance can lead to catastrophic failure.
Damping in Structures
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let’s talk about damping in structures. What types of damping can you name?
There’s viscous damping and hysteretic damping.
Correct! How do you think the damping ratio affects the peak response?
More damping reduces the peak response, right?
Exactly! Damping helps to dissipate energy dissipating and lessens the impact of oscillations during an earthquake.
Numerical Methods for Solving Motion Equations
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
To solve the equation of motion, we often rely on numerical methods like Newmark-beta, Wilson-θ, and Runge-Kutta. Who is familiar with any of these methods?
I have heard of Runge-Kutta; it's used for solving differential equations, right?
That's correct! These methods break the motion into small time steps, allowing us to compute displacement and velocity iteratively. Why do you think it's necessary to use numerical methods in this context?
Because the equations might be too complex to solve analytically?
Exactly! For complex structures and ground motions, numerical methods are essential for accurate analysis.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section outlines the equations of motion for single-degree-of-freedom systems, discusses the elastic and inelastic responses to seismic forces, emphasizes the role of damping in structural response, and introduces numerical methods used to solve these equations, providing a comprehensive understanding of how structures respond dynamically during earthquakes.
Detailed
Dynamic Response of Structures
In earthquake engineering, analyzing how structures respond to dynamic loading is critical. This section begins by presenting the equation of motion for a Single Degree of Freedom (SDOF) system given by:
mx¨(t)+cx˙(t)+kx(t)=−mu¨(t)g
where u¨g(t) is the ground acceleration.
Next, it discusses different types of structural responses:
- Elastic Response: Structures that return to their original shape after loading.
- Inelastic Response: Structures that may exhibit permanent deformations.
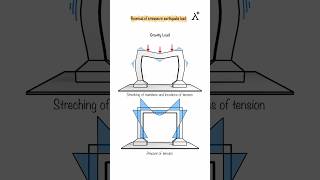
- Resonance Conditions: Situations where the frequency of ground motion matches the natural frequency of the structure, which can lead to significant amplification of response.
The section also elaborates on damping in structures, identifying various types (e.g., viscous and hysteretic), and explains how the damping ratio influences the peak structural response during an earthquake.
Finally, numerical methods such as Newmark-beta, Wilson-θ, and Runge-Kutta for solving the equation of motion are introduced, highlighting how these methods compute displacement, velocity, and acceleration at each time step. This thorough understanding of dynamic response is foundational to effective seismic design and response control.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Equation of Motion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For a Single Degree of Freedom (SDOF) system:
mx¨(t)+cx˙(t)+kx(t)=−mu¨ (t)
g
where
u¨g(t) is ground acceleration.
Detailed Explanation
The equation of motion describes how an SDOF system reacts to dynamic forces such as those caused by earthquakes. Here, 'm' represents the mass of the structure, 'c' is the damping coefficient that measures how much energy is dissipated as the structure moves, and 'k' is the stiffness of the structure indicating its resistance to deformation. The term −müg(t) represents the external forces acting on the structure due to ground acceleration, which is driven by seismic activity. Thus, the equation collectively illustrates how these elements combine to influence structural behavior during an earthquake.
Examples & Analogies
Think of a swing at a playground. When pushed (applying a force), it not only swings (moves) but also has a certain weight (mass) that affects how high it goes. If the swing has springs (stiffness) and is gently brought back to rest before being pushed again (damping), it’ll swing differently than if it were a rigid object with no give. Similarly, structures respond to ground movement according to how much they can 'give' and how heavy they are.
Types of Structural Response
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Elastic Response
• Inelastic Response
• Resonance Conditions
Detailed Explanation
When structures are subject to dynamic loads, they can respond in different ways. An elastic response refers to the behavior of structures that return to their original shape after the load is removed. In contrast, an inelastic response involves permanent deformations, where some energy is absorbed by the material and not returned. Resonance conditions occur when the frequency of the ground motion matches the natural frequency of the structure, significantly amplifying the response and potentially leading to failure.
Examples & Analogies
Imagine a child on a swing again. If you push the swing at just the right moment (corresponding to its natural swinging frequency), the child goes higher and higher—this is similar to resonance. If the swing is never pushed strongly enough, it stays within a safe range, demonstrating elastic response. However, if the child decides to swing out too far and falls off, that represents inelastic behavior—something has changed permanently.
Damping in Structures
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Types: Viscous damping, Hysteretic damping.
• Effect of damping ratio on peak response.
Detailed Explanation
Damping is crucial in mitigating the oscillations that occur in structures during an earthquake. Viscous damping refers to the energy that is dissipated through motion of a fluid, while hysteretic damping refers to energy loss due to the material's behavior under stress (how the material deforms). The damping ratio is a measure of the damping effect relative to critical damping; it significantly impacts how much the building will sway and how quickly it will return to equilibrium after shaking.
Examples & Analogies
When you go down a slide, a viscous damper works like moist sand that slows you down as you reach the end. If the slide is made of a rough material that catches you (like hysteretic damping), it provides a different experience—both types help ensure that you land safely at the bottom rather than flying off uncontrollably!
Numerical Methods for Solving Equation of Motion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Time stepping methods: Newmark-beta, Wilson-θ, Runge-Kutta.
• Displacement, velocity, and acceleration computed at each time step.
Detailed Explanation
To understand how structures respond dynamically, numerical methods are employed to solve the complex equations of motion. Time stepping methods, such as Newmark-beta and Runge-Kutta, discretize the problem over small time intervals, computing the displacement, velocity, and acceleration at each step based on the previous step's values. This iterative process allows engineers to simulate the dynamic response of structures due to ground motion accurately.
Examples & Analogies
Imagine driving a car: you don’t turn the wheel suddenly but instead make gradual adjustments in small increments. Similarly, numerical methods make small adjustments at each time interval to predict where the structure will be at the next moment based on current conditions, ensuring smooth and achievable predictions rather than abrupt and unrealistic changes.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Dynamic Response: The behavior of structures subjected to time-varying loads (like earthquakes).
-
Equations of Motion: Mathematical formulas that describe the dynamic behavior of structures.
-
Damping: Mechanisms to dissipate energy and reduce peaks in structural response.
-
Types of Responses: How structures respond can vary, mainly categorized into elastic and inelastic responses.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A building swaying back to its original position after an earthquake illustrates elastic response.
-
A bridge that has permanent deformations after a strong earthquake exemplifies inelastic response.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When ground shakes and structures sway, remember damping saves the day.
📖 Fascinating Stories
-
Imagine a tall building during an earthquake, swaying side to side like a dancer. It uses damping to control its movements and not fall over.
🧠 Other Memory Gems
-
Remember the acronym DER: Damping, Elastic, Resonance to recall the key types of structural responses.
🎯 Super Acronyms
Using DAMP for Damping, Acceleration, Motion, and Peak helps remember key concepts of dynamic response.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Elastic Response
Definition:
The temporary deformation of a structure that returns to its original shape after load removal.
-
Term: Inelastic Response
Definition:
The permanent deformation of a structure that does not return to its original shape after loading.
-
Term: Damping
Definition:
The process through which energy is dissipated in a structure, reducing vibrations.
-
Term: Resonance
Definition:
A condition occurring when the frequency of external excitation matches a structure's natural frequency, potentially amplifying its response.
-
Term: Numerical Methods
Definition:
Mathematical techniques for approximating solutions to complex equations, commonly employed in dynamic analysis.