Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to MDOF Systems and Equations of Motion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to discuss the response of multi-degree-of-freedom or MDOF systems. First, let’s go over the basic equation of motion, which is crucial for analyzing these systems during seismic events. Does anyone remember what the general form looks like?
Is it the one with mass, damping, and stiffness matrices?
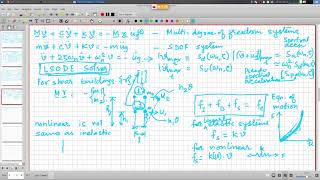
Exactly! The equation is $$[M]{x¨(t)}+[C]{x˙(t)}+[K]{x(t)}=-[M]{u¨(t)}_g$$. The matrices represent mass, damping, and stiffness respectively. Let's break down what each term signifies.
So, what does u_g(t) represent?
Good question! {u_g(t)} is the ground motion input. It's essential to understand the foundation of our response. Remember, MDOF systems are more realistic compared to single-degree-of-freedom systems.
Modal Analysis
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we understand the equation of motion, let’s talk about modal analysis, which simplifies our calculations. Can anyone explain what we mean by transforming coupled equations using mode shapes?
Does that mean we're breaking it down to a simpler form?
Exactly! We can express our system in terms of its mode shapes, which allows us to uncouple the equations. This borrowing leads to easier calculations of the dynamic response.
What’s the significance of the mode shapes in this process?
Great question! The mode shapes determine how the structure will deform under seismic loading, and they help us identify critical responses during analysis. Always remember: simple is better!
Mode Participation Factor and Modal Mass
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s delve into the mode participation factor. How do you think we can quantify how much each mode contributes to the total response of an MDOF system?
Isn’t that where we talk about modal mass?
Right on target! The modal mass quantifies the mass participating in each mode. It allows us to evaluate which modes are essential for our structure’s response. This is fundamental for efficient design in earthquake-prone areas.
What happens if the modal mass is higher for certain modes?
Great inquiry! If certain modes have a higher modal mass, they significantly influence the structure's overall response to seismic events. It means those modes need to be carefully considered during design.
Orthogonality of Modes
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Finally, let's touch on the orthogonality of modes. Can anyone explain why this is significant?
Does it help make the equations easier to solve?
Exactly! The orthogonality condition simplifies calculations and lets us treat each mode separately without interference from the others.
So it’s like isolating symptoms when diagnosing a problem?
Precisely! By isolating modes, we ensure clarity in our analysis, making it easier to understand complex behavior during earthquakes.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the equations of motion governing MDOF systems, techniques such as modal analysis and participation factors, and response spectrum methodologies. Understanding these concepts is vital for engineers tasked with designing structures capable of withstanding seismic forces.
Detailed
Detailed Summary
The response of multi-degree-of-freedom (MDOF) systems is essential in understanding the behavior of complex structures during earthquakes. This section begins with the equation of motion for MDOF systems given by:
$$[M]{x¨(t)}+[C]{x˙(t)}+[K]{x(t)}=-[M]{u¨(t)}_g$$
where [M], [C], and [K] represent the mass, damping, and stiffness matrices, respectively, and {u_g(t)} is the ground acceleration vector. The discussion emphasizes the importance of modal analysis, which enables the transformation of these coupled equations into simpler, uncoupled forms using the mode shapes of the system.
We delve into the modal analysis process, which includes calculating the mode participation factor and modal mass to quantify how much each mode contributes to the system's overall response. The orthogonality of modes is also discussed, providing a mathematical framework that simplifies analysis.
Furthermore, the section introduces the response spectrum method tailored for MDOF systems, explaining how modal responses can be computed separately with combination rules like Square Root of the Sum of the Squares (SRSS) and Complete Quadratic Combination (CQC). This holistic approach to MDOF systems is crucial for engineers engaged in structural analysis and design, particularly in regions susceptible to seismic activity.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Equation of Motion for MDOF
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The equation of motion for a Multi-Degree-of-Freedom (MDOF) system is expressed as:
$$[M]\{x¨(t)\}+[C]\{x˙(t)\}+[K]\{x(t)\}=−[M]\{u¨(t)\}_g$$
Detailed Explanation
The equation of motion is fundamental to understanding how MDOF systems behave under dynamic loads, such as seismic movements. In this equation:
- $$[M]$$ is the mass matrix that represents the mass distribution of the structure.
- $$[C]$$ is the damping matrix, which accounts for energy dissipation in the system.
- $$[K]$$ is the stiffness matrix, which determines the resistance of the structure to deformation.
- $$\{x(t)\}$$ is the displacement vector, indicating how different points in the structure move during an earthquake.
- $$\{u¨(t)\}_g$$ represents the ground acceleration, which is what induces motion in the structure. The equation reflects how all forces acting on the structure result in a resultant motion.
Examples & Analogies
Imagine a multi-story building during an earthquake. Each floor can move independently, just like how multiple vehicles on a road might jolt differently when there’s a sudden bump. The equations help engineers predict how each floor (or vehicle) reacts to the ground shaking, ensuring that designs can handle these movements safely.
Modal Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Modal analysis involves transforming coupled equations into uncoupled equations using mode shapes. The mode superposition method is utilized.
Detailed Explanation
Modal analysis is a technique used to simplify the analysis of complex structures. By using mode shapes, which are the characteristic shapes that a structure takes at different natural frequencies, engineers can break down the MDOF system into simpler, uncoupled equations. This allows for easier calculations, as each mode can be analyzed independently before combining them to get the overall response of the structure. The mode superposition method is a mathematical technique where the total response is approximated by summing the contributions of each individual mode, weighted by its participation in the dynamic behavior.
Examples & Analogies
Think of a group of friends dancing together. Each friend has their own style (mode) of dancing. If you’re trying to evaluate how the group as a whole expresses itself, you can observe each friend separately and then combine their different moves (modal responses) to see the entire dance. This is much like how modal analysis allows engineers to assess the complex response of buildings by looking at simpler modes of vibration.
Mode Participation Factor and Modal Mass
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The mode participation factor quantifies how much each mode contributes to the total response.
Detailed Explanation
In MDOF analysis, not all modes contribute equally to the structural response under seismic loading. The mode participation factor is a measure that indicates the relative contribution of each mode to the overall response of the structure. Modal mass refers to the effective mass participating in each mode. Engineers calculate these factors to understand which modes are most significant during vibrations caused by an earthquake, allowing for focused design improvements on those critical modes to enhance safety and performance.
Examples & Analogies
Imagine a band where each musician plays a different instrument. If the drummer is stronger or louder than the others, they will have a greater influence on the overall sound. Similarly, the mode participation factor helps engineers identify which 'musicians' (modes) in a building’s design are most critical to its performance during an earthquake.
Orthogonality of Modes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This principle refers to a mathematical simplification that arises from the orthogonality of mode shapes.
Detailed Explanation
Orthogonality of modes in structural dynamics implies that the mode shapes are mathematically independent of each other. This independence simplifies the analysis because it allows engineers to analyze each mode separately without interference from others. In essence, when a structure vibrates, the different modes do not affect one another, making calculations more straightforward. This principle is crucial for employing modal analysis in MDOF systems effectively.
Examples & Analogies
Consider learning different dance forms—like ballet and hip-hop. While learning ballet, you focus entirely on that style without mixing in hip-hop moves. Just like this, the orthogonality of modes ensures that each mode can be studied independently, leading to clearer, more manageable results in structural analysis.
Response Spectrum Method for MDOF
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In the response spectrum method, modal responses are computed separately using defined rules such as SRSS (Square Root of the Sum of the Squares) and CQC (Complete Quadratic Combination).
Detailed Explanation
The response spectrum method is a powerful tool used to evaluate the response of MDOF structures to seismic loading. In this method, the response of each mode is calculated individually, and the total response is obtained by combining these modal responses through specific rules. The Square Root of the Sum of the Squares (SRSS) method and the Complete Quadratic Combination (CQC) method are two common techniques to combine these modal responses, allowing engineers to obtain a comprehensive understanding of a structure’s performance under earthquake conditions.
Examples & Analogies
Imagine a team of athletes competing in a multi-event sport, like a decathlon. Each athlete (mode) has their own event where they perform individually (modal response). To assess the team's overall performance, you might combine their scores from each event using a scoring system (SRSS or CQC) to see how they stack up as a team rather than looking at singular performances in isolation.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
MDOF Systems: Structures with multiple degrees of freedom whose response is influenced by dynamic loads.
-
Modal Analysis: Analytical approach to simplify the equations of motion for complex systems using mode shapes.
-
Participation Factor: A coefficient representing the extent to which each mode contributes to the overall response.
-
Modal Mass: Mass associated with specific modes that influences a structure's response.
-
Orthogonality: A condition that helps simplify calculations by ensuring that mode shapes do not influence one another.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For a 5-story building during an earthquake, the first mode may primarily involve sway of the entire structure, while higher modes may reflect more complex deformations.
-
A multi-story parking garage can exhibit MDOF behavior as different stories vibrate at different frequencies when subjected to seismic activity.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In MDOF systems, we break it all down, / With modes that dance and wear a crown.
📖 Fascinating Stories
-
Once upon a time, in a skyscraper tall, various modes of motion had their ball. Each mode had a role, from sway to twist, together they worked so that none were missed.
🧠 Other Memory Gems
-
Remember the acronym 'MOM' for MDOF: Mass, Orthogonality, Modes.
🎯 Super Acronyms
MOP
- MDOF
- Orthogonality
- Participation allows understanding of dynamic response.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: MDOF Systems
Definition:
Multi-Degree-of-Freedom Systems involve structures with more than one point of movement, complicating their response under dynamic loads.
-
Term: Modal Analysis
Definition:
A method used in structural engineering to decompose complex motion into simpler, independent modes.
-
Term: Mode Participation Factor
Definition:
A value that quantifies the share of each mode in the total response of a system.
-
Term: Modal Mass
Definition:
Mass associated with a specific mode shape that participates in dynamic response.
-
Term: Orthogonality of Modes
Definition:
A mathematical condition ensuring that mode shapes are independent from one another, simplifying analysis.