Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Causes of Nonlinearity
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we're going to discuss nonlinear structural response, specifically what causes it. It’s predominantly due to material nonlinearity, like when steel yields, and geometric nonlinearity, which occurs in the presence of large displacements. Who can explain what we mean by material nonlinearity?
Material nonlinearity happens when the material exceeds its yield stress, right?
Exactly! As materials yield, they do not return to their original form, changing their strength threshold. Now, Student_2, can you share what geometric nonlinearity implies?
It means that the shape and displacement of the structure change significantly, affecting how forces are distributed.
Great! Remember the acronym **GEM** for Geometric effects can affect materials — Geometry, Elasticity, and Material yield. Let’s move on to the different hysteresis models.
Idealized Hysteresis Models
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now we will discuss idealized hysteresis models. Can someone explain what a bilinear model is?
It's a simplified model that represents the structure's response with two linear segments rather than capturing every detail.
Correct! Bilinear models are commonly used due to their simplicity. How about the Takeda model, Student_4?
It accounts for the cyclic unloading and reloading behavior, making it more realistic for structures under cyclic loading.
Exactly! Using **T-F-B** for Takeda, Friction, and Bilinear can help you remember these models. Finally, the Bouc-Wen model provides a robust framework for capturing nonlinearities. What does that suggest, Student_1?
It suggests we can simulate more complex nonlinear behaviors effectively with this model.
Time-History Analysis
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s shift our focus to time-history analysis. How does this differ when using nonlinear models versus linear models?
Nonlinear models require more complex numerical integration methods because we have to account for varying material responses over time.
Exactly! Nonlinear analysis like this often involves step-by-step techniques to assess how structures react over time. What’s the significance of understanding this response during seismic events, Student_3?
It tells us how structures will behave under real earthquake conditions, which is crucial for safety.
Perfect! Remember the phrase **'Time is of the Essence'** to signify the importance of temporal analysis in earthquake engineering.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Nonlinear structural response arises from material and geometric nonlinearity during seismic events. This section explores idealized hysteresis models that capture such behavior, followed by an overview of time-history analysis that employs numerical methods for integrating ground motions and assessing structural response.
Detailed
Nonlinear Structural Response
Understanding nonlinear structural response is crucial for accurately assessing how structures behave during earthquakes. This phenomenon can be attributed mainly to two factors: material nonlinearity and geometric nonlinearity. Material nonlinearity occurs when materials yield (for example, steel yielding under stress), while geometric nonlinearity is evident when large displacements affect the system's behavior.
Idealized Hysteresis Models
Various idealized hysteresis models are used to characterize the behavior of structures under large deformations:
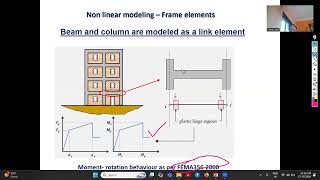
1. Bilinear Models: These models simplify the complex response into two linear segments, offering an effective approximation for many materials.
2. Takeda Models: This model accounts for hysteresis loops by representing the unloading and reloading behavior, providing a more accurate depiction of cyclic response.
3. Bouc-Wen Models: This sophisticated model captures various forms of nonlinear behavior by using additional mathematical terms and parameters.
Time-History Analysis with Nonlinear Models
Time-history analysis for nonlinear models is complex and involves step-by-step numerical integration techniques. This approach allows engineers to simulate and study the actual response of structures over time when subjected to specific ground motions. Unlike linear analysis, nonlinear methods provide insight into how structures may experience yielding and deformations under seismic loading. This analysis is paramount in ensuring structural integrity and safety during earthquakes.
Youtube Videos
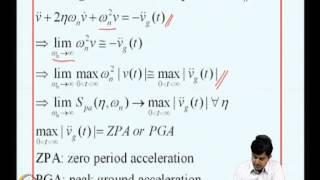
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Causes of Nonlinearity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Causes of Nonlinearity
- Material nonlinearity (e.g., yielding of steel).
- Geometric nonlinearity (e.g., large displacements).
Detailed Explanation
Nonlinearity in structures occurs due to two main factors: material nonlinearity and geometric nonlinearity. Material nonlinearity arises when structural materials, such as steel, reach their yield point and start to deform plastically, meaning they do not return to their original shape after the load is removed. Geometric nonlinearity comes into play when the structure undergoes large displacements. In such cases, the assumptions of small deformations used in linear analysis no longer hold true, affecting how the structure behaves under loads.
Examples & Analogies
Think of a rubber band. When you stretch it gently, it follows Hooke's Law (linear behavior) and returns to its original shape. However, if you stretch it too far, it will lose its ability to resume its shape (material nonlinearity). Similarly, if you twist a structure significantly (like bending a flexible straw), the way forces act on it changes, representing geometric nonlinearity.
Idealized Hysteresis Models
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Idealized Hysteresis Models
- Bilinear, Takeda, Bouc-Wen models.
Detailed Explanation
Idealized hysteresis models are simplified representations of how structures respond to cyclic loading. The bilinear model represents a structure that behaves elastically until it reaches a yield point, after which it exhibits a constant stiffness during yielding. The Takeda model captures the degrading behavior of materials during repeated loading and unloading cycles. The Bouc-Wen model is more complex and can simulate different types of hysteretic behavior, allowing for more accurate predictions of structural response under seismic loads.
Examples & Analogies
Imagine you have a spring (bilinear) that stretches easily until it reaches a limit, making it harder to pull further. The Takeda model is like a sponge that behaves differently based on how much you squeeze it repeatedly (degrading with each squeeze). The Bouc-Wen model is similar to how a trampoline behaves under varying weights—its response changes based on the weight and how quickly it is applied.
Time-History Analysis with Nonlinear Models
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Time-History Analysis with Nonlinear Models
- Requires step-by-step integration using numerical methods.
Detailed Explanation
Time-history analysis is a method for evaluating the dynamic behavior of structures under seismic loading. When dealing with nonlinear models, it requires step-by-step integration, meaning the analysis is done incrementally over time. This technique allows engineers to capture the evolving response of a structure subjected to ground motion in a more detailed manner than simplified methods. Numerical methods, such as the Newmark method or Runge-Kutta methods, are often employed to perform these calculations iteratively.
Examples & Analogies
Think of watching a movie frame by frame. Each frame represents a moment in time, and when played in sequence, it shows the full motion of the story. Time-history analysis works similarly—by analyzing how a structure reacts at each moment during an earthquake, engineers can get a detailed picture of how the structure will perform over the duration of the seismic event.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Nonlinear Structural Response: Refers to the complex behavior of structures under large deformation and loads.
-
Material and Geometric Nonlinearity: The two main causes of nonlinear responses in structures due to material yielding and large displacements.
-
Hysteresis Models: Mathematical models designed to describe how materials behave under cyclic loading conditions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A steel beam that deforms significantly under an earthquake load exhibits material nonlinearity as it yields, creating a permanent bend.
-
A building experiencing large lateral displacement during an earthquake showcases geometric nonlinearity as it changes shape.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In the realm where buildings sway, nonlinear responses come into play.
📖 Fascinating Stories
-
Imagine a flexible building during an earthquake, bending with the waves while accounting for every twist and turn, resembling a dancer in sync with the music.
🧠 Other Memory Gems
-
Use B-T-B (Bilinear, Takeda, Bouc-Wen) to remember the key hysteresis models!
🎯 Super Acronyms
Remember **GEM** (Geometry, Elasticity, Material yield) for nonlinearity factors.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Material Nonlinearity
Definition:
The behavior of materials that change upon exceeding yield stress, resulting in permanent deformation.
-
Term: Geometric Nonlinearity
Definition:
Changes in geometry of structures due to large displacements that affect the load response.
-
Term: Hysteresis Models
Definition:
Mathematical models used to describe the nonlinear behavior of materials and structures during cyclic loading.
-
Term: Bilinear Model
Definition:
A simplified hysteresis model that comprises two linear segments representing loading and unloading behavior.
-
Term: Takeda Model
Definition:
A model capturing cyclic behavior of materials accounting for both loading and unloading phases in hysteresis.
-
Term: BoucWen Model
Definition:
A sophisticated model used for simulating various types of nonlinear behavior in materials.
-
Term: TimeHistory Analysis
Definition:
A numerical technique that evaluates dynamic responses based on actual ground motion records over time.