Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Steady State Assumption
Unlock Audio Lesson
Today we will explore the steady state assumption. This is a fundamental concept in environmental science, particularly when calculating pollutant dispersion. Can anyone tell me what they understand about this assumption?
I think it means that the concentration of pollutants doesn’t change with time.
Exactly! In a steady state, while the concentration may vary across different locations, it remains constant over time. This simplifies our calculations significantly.
But what if the emission rates change?
Good question! If emissions or other parameters fluctuate, the steady state assumption no longer applies. Let's remember this with the acronym C. S. E. - Constant Source Emission.
So, we can’t use this model if things are changing?
Correct! We'll explore how to identify when this assumption is valid and when it’s not.
Mass Conservation in Plume Modeling
Unlock Audio Lesson
Now that we know about the steady state assumption, let's discuss mass conservation in plumes. What does this mean?
I think it means the total mass of pollutants released is preserved in the plume?
Correct! The mass released must equal the mass present in the plume. This is essential for understanding dispersion. If the emission rate is Q, how do we represent this mathematically?
We can use the equation Q equals u multiplied by the volume dimensions, right?
Spot on! You're all catching on quickly!
Gaussian Distribution and Steady State
Unlock Audio Lesson
Lastly, let's connect the steady state assumption to the Gaussian distribution model. How are they related?
Is the Gaussian distribution used because it represents how pollutants spread through the air?
Yes! The Gaussian model assumes a certain spread of pollutants, and the highest concentration tends to be near the center of the plume.
What effects the width of that spread?
Factors like emission height and weather conditions. Let’s remember: W.H.A., which stands for Width is dependent on Height and Atmospherics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the steady state assumption is introduced as a critical concept in understanding pollutant dispersion in an environment. This assumption allows models to predict concentration levels without accounting for time-based changes, provided emission rates and other environmental factors remain constant.
Detailed
Steady State Assumption
The steady state assumption is a crucial concept used in dispersion modeling, particularly the Gaussian dispersion model. It states that the concentration of a pollutant at any location remains unchanged over time, allowing for simplifications in calculations. To uphold this assumption, emission rates and environmental properties must remain constant. If any parameter alters over time, the steady state assumption cannot be applied. This section discusses how this assumption allows for average values and standard deviation to determine the expected range of concentrations.
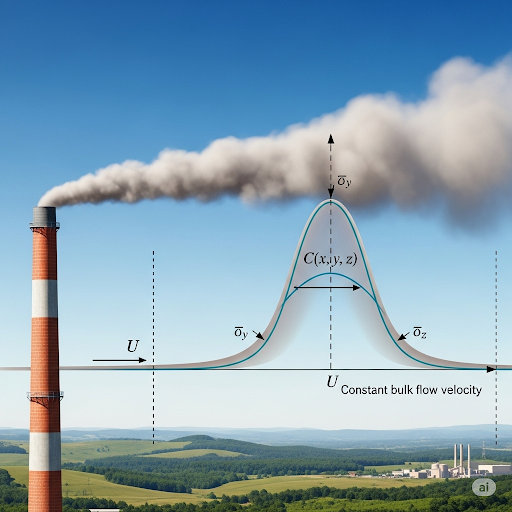
Additionally, the conversation explores how bulk flow affects dispersion calculations and simplifies modeling. The concept of mass conservation within a plume is explained, emphasizing that the total mass present equals the pollutant release rate integrated over the plume's volume. The section concludes by touching on the relation between the Gaussian distribution of pollutants and the steady state model, illustrating how the characteristics of dispersion can be modeled effectively.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Steady State Assumption
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We make two assumptions, one is a steady state assumption you don’t have to do this but for that Gaussian dispersion model that we generally present we use the steady state assumptions where we say \( \frac{dC}{dt} = 0 \), which means that at any point in time the concentration is the same; at any location you measure it, concentration will not change with time.
Detailed Explanation
The steady state assumption is a fundamental concept in modeling where the concentration of a substance remains constant over time. In this context, \( \frac{dC}{dt} = 0 \) implies that at any given point in the environment, if we measure the concentration of a pollutant, it stays the same (does not change as time progresses). However, concentration can still vary by location, meaning that while some places may have more of the pollutant, it won’t increase or decrease over time at those specific locations.
Examples & Analogies
Imagine a bathtub with the tap running while the drain is also open. If the water level remains constant (steady state), it means that the water flowing in equals the water flowing out, leading to a consistent level over time, although the location of the water will change until the tap is turned off.
Conditions for Steady State
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
It will be different with space but it will not change with time, ok. So, if you are looking at it in a plume nothing is going to change, which means for this to be true, everything else has to be true: the emission has to be constant; the properties have to be constant.
Detailed Explanation
For the steady state assumption to hold true, certain conditions must be met. The emission of pollutants into the air must be constant, meaning the source of pollution isn't varying with time. Similarly, the physical properties of the pollutants and the environment (like wind speed and temperature profiles) must also remain unchanged. If any of these factors fluctuate over time, the steady state assumption is invalidated, and we can no longer consider concentrations steady.
Examples & Analogies
Think about the air quality in a factory. If the machines are running at a constant rate and emissions are steady, the air quality measurements will remain steady too. However, if one day a machine starts malfunctioning or if workers increase production, emissions will vary, making the air quality different from previous measurements.
Assumption of Averaging Values
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If something changes... changes with time, then this is not true. You cannot use a steady state assumption. So, which means it is an assumption that in an environment nothing is constant.
Detailed Explanation
The essence of the steady state assumption is that in a real-world scenario, conditions can continuously change. Therefore, to simplify calculations and predictions, researchers often rely on average values of various factors and their standard deviations. This means they accept that fluctuations exist, but they seek to understand the overall trend or typical conditions through averaging.
Examples & Analogies
Consider measuring the temperature in a bakery. While the temperature might fluctuate every minute due to ovens being opened, on average, the temperature during baking remains around a certain value. This average helps bakers know when to expect the best results for their products, despite the fluctuations.
Simplification of Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now here we neglect the dx term, so this entire thing reduces to this simpler equation.
Detailed Explanation
When we apply the steady state assumption, we can simplify complex equations by neglecting certain terms that become irrelevant in a steady state scenario. By reducing our equations, we can focus on the most significant factors that influence pollutant dispersal, making it easier to understand and model how pollutants spread in different environments.
Examples & Analogies
Think of simplifying a recipe by ignoring optional spices that won't change the dish's overall flavor. You can focus on the primary ingredients—like flour and sugar—to create the main product. Similarly, neglecting less significant variables allows us to concentrate on the primary factors affecting concentration.
General Solutions and Integration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is a general solution for this equation; the solutions are already there... we club all of them into this constant.
Detailed Explanation
In deriving a general solution for the Gaussian dispersion model, multiple constants associated with dimensions and conditions are combined into a single constant. This streamlining of variables facilitates easier calculations and constructs a cohesive model that adheres to the boundary conditions (i.e., environmental limits). It helps us derive the essential relationships between concentration and time without getting bogged down by the many variables at play.
Examples & Analogies
Think of combining different ingredients in cooking to simplify a dish. Instead of measuring every individual spice every time, a cook may create a blended spice mix that represents a majority of flavors, saving time and ensuring a consistent flavor every time a dish is prepared.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Steady State Assumption: The principle that pollutant concentration remains constant in time.
-
Mass Conservation: Critical for calculating total pollutant mass in dispersion modeling.
-
Gaussian Distribution: A model used to represent how pollutants are dispersed in the atmosphere.
-
Dispersion Characteristics: Influenced by environmental factors and source characteristics.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of steady state assumption is when a factory emits pollutants at a constant rate over a fixed period, allowing for reliable modeling of air quality.
-
In Gaussian dispersion, the maximum pollutant concentration is typically found at the plume center, diminishing as one moves away from this central point.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In the steady state, emissions don’t rotate; concentration’s fate is left to create.
📖 Fascinating Stories
-
Imagine a factory that never changes its output. Like magic, the air around stays still, filling and spilling where needed, ensuring we can predict what happens next at any place and time.
🧠 Other Memory Gems
-
C.S.E. - Constant Source Emission helps remember that a steady state means no change over time.
🎯 Super Acronyms
W.H.A. - Width from Height & Atmospherics, to recall factors influencing dispersion.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Steady State Assumption
Definition:
The assumption that the concentration of pollutants remains constant over time at any given location in a model.
-
Term: Gaussian Distribution
Definition:
A statistical distribution that describes how concentrations of pollutants typically spread in the atmosphere; often visualized as a bell curve.
-
Term: Mass Conservation
Definition:
The principle that the total mass of a closed system remains constant over time, which is fundamental in calculating pollutant dispersion.
-
Term: Dispersion
Definition:
The process through which pollutants spread through the air or water, typically affected by environmental factors.