Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Bernoulli’s Equations
Unlock Audio Lesson
Today, we will begin with Bernoulli’s equations. Remember, Bernoulli's principle states that as the speed of a fluid increases, its pressure decreases. Can anyone recall some applications of Bernoulli's principle?
Airplanes use it to generate lift!
And it’s also used in venturi meters to measure flow rates.
Exactly! When applying Bernoulli’s equations, we often consider factors like fluid velocity, pressure, and elevation. Let’s also remember the acronym 'PVE' which stands for Pressure, Velocity, and Elevation. Can anyone tell me how these factors are interconnected?
Higher velocity means lower pressure!
Perfect! Now let's discuss how these concepts integrate into solving fluid dynamics problems.
Applying the Reynolds transport theorem
Unlock Audio Lesson
Now let's dive deeper into the Reynolds transport theorem. What does it help us achieve in fluid dynamics?
It helps us relate the flow of mass and momentum across control volumes!
That's correct! We can compute the influx and outflux of momentum to determine changes in motion. Remember, the total force applied is equal to the change in momentum across the control volume. Can you think of how we might express this mathematically?
Is it similar to Newton’s second law?
Yes! It can be viewed through the lens of Newton’s laws. Let’s try to apply it to a scenario with fluid flow. What would the equations look like?
Solving Fluid Flow Scenarios
Unlock Audio Lesson
Let's put our knowledge into practice. Consider we have a horizontal jet striking a vertical plate. How would we apply Bernoulli's equation here?
We’ll analyze two points along the streamline and apply Bernoulli’s equation.
Exactly! From point 1 to point 2, if we neglect impact losses, how can we relate pressure and velocity?
We can say the velocity at point 1 is equal to the velocity at point 2!
Good thinking! This uniformity will help us simplify our calculations significantly. Let’s work through the numerical solution together.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the practical application of Bernoulli’s equations to analyze fluid flow scenarios, emphasizing the use of the Reynolds transport theorem alongside linear momentum equations. We also solve specific examples to illustrate how these principles govern fluid mechanics.
Detailed
Applying Bernoulli’s Equations
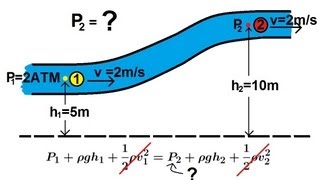
In section 2.2, we delve into the application of Bernoulli’s equations under steady-state flow conditions on a horizontal surface, where the vertical height (z) remains constant. The primary focus is to use Bernoulli's principles in conjunction with linear momentum equations to derive flow parameters, such as discharge (Q) and force components acting on fluid interfaces.
Key Points:
- Reynolds Transport Theorem: This theorem is foundational for simplifying dynamic systems involving mass and momentum changes within control volumes.
- Bernoulli’s Equation: The equation relates pressure, velocity, and elevation in fluid flow, crucial when analyzing fluid movement through pipes or jets.
- Examples Solved: The section includes solving problems related to momentum flux and flow angle (theta) in impact scenarios, guiding problem solvers through real-world applications of the mathematical concepts.
By understanding these principles, students gain essential tools for analyzing fluid systems relevant to engineering and physics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Bernoulli’s Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
And here as you know it we have considered it is a horizontal surface. So z equal to z₁. That is what we cancelled out. And we are just substituting the mass conservation equation and the Bernoulli’s equations to compute what will be the Q value.
Detailed Explanation
In this chunk, we set the foundation for using Bernoulli’s equations. We consider a scenario where the surface is horizontal, meaning the vertical height (z) at two points is the same (z₁). This simplification allows us to focus on how to apply mass conservation and Bernoulli’s principles to find the flow rate (Q). This is critical in fluid dynamics where understanding flow rates helps engineer systems like pipes or jet streams.
Examples & Analogies
Imagine you are watering your garden with a hose. If you hold the hose level (a horizontal surface), you can better predict how far the water will spray without worrying about the height, allowing you to adjust the nozzle for the best flow.
Linear Momentum Equations Application
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We are going to apply linear momentum equations. Let us apply the linear momentum equations for these problems. And always I encourage that, please start applying the Reynolds transport theorems.
Detailed Explanation
This chunk emphasizes the importance of linear momentum equations in analyzing fluid flow. By applying Reynolds transport theorems, we can transform basic momentum equations into more simplified forms that allow us to assess how forces act within a fluid system. Essentially, we calculate the momentum influx and outflux to understand how they affect the forces experienced by the system.
Examples & Analogies
Think of a basketball player dribbling a ball. The forces they apply change as they move the ball (momentum influx) compared to when they release it (momentum outflux). Understanding how these forces work helps the player maintain control over the game.
Momentum Flux Calculations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We can write that the sum of the force is acting is equal to the momentum influx minus the momentum outflux. Since it is a steady flow conditions, the change equals zero.
Detailed Explanation
Here, we delve deeper into calculating momentum flux, which involves assessing the forces acting on a control volume. By understanding that the sum of forces equals zero under steady flow conditions, we can conclude that the momentum going in must equal the momentum coming out. This balance is fundamental in fluid mechanics as it lays the groundwork for predicting flow behavior.
Examples & Analogies
Think of a revolving door. While one person enters (momentum influx), another exits (momentum outflux). For the door to move smoothly, the number of people entering must match those leaving — the system remains balanced.
Calculating Resultant Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So we will play along the x directions to get it. If I apply in the x direction, we will get the sum of the force F_x will be...
Detailed Explanation
In this segment, we focus on calculating the resultant forces in the x-direction based on momentum flux components. This is achieved by substituting specific values related to pressure, area, and flow rate, which helps us derive the force experienced by the fluid in that direction. The equations become specific, allowing us to calculate numerical values, reinforcing the theoretical principles.
Examples & Analogies
Picture pushing a swing. The force you exert (F_x) determines how high it swings. By calculating the force correctly, you can achieve the desired height and movement for the swing.
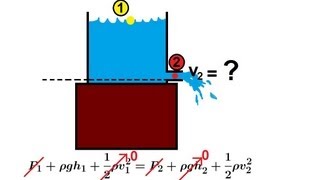
Example Problem: Horizontal Jet Impact
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In this case there is a horizontal jet of the flow with angle theta strike on a vertical plate... if we consider is a control volume like this.
Detailed Explanation
This chunk introduces a practical example where a horizontal jet of fluid impacts a vertical plate, and the flow conditions are analyzed using Bernoulli's equations and linear momentum. We define the problem, set up our equations, and apply them to predict the value of theta. Such examples reveal how theoretical principles can be applied to solve real-world engineering problems.
Examples & Analogies
Imagine water spraying from a garden hose (the jet) hitting a wall (the plate). Adjusting how you hold the hose changes the angle of the water flow, much like changing theta in our equations alters the analysis.
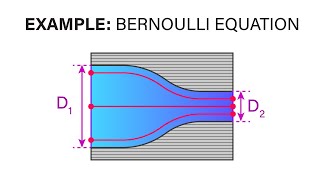
Flow Through a Venturi Meter
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In this case, there is a venturimeter... and we can apply the Bernoulli’s equations along this streamlines.
Detailed Explanation
In this section, we analyze flow through a venturi meter, a device used to measure fluid flow rates. By applying Bernoulli’s equations, we calculate theoretical values and compare them to actual flow rates to determine the discharge coefficient. This application showcases how Bernoulli's principles aid in designing devices that measure and regulate flow effectively.
Examples & Analogies
Consider a narrowing section of a water slide. As the slide narrows, water speeds up, just as flow speeds up in the venturi meter. Measuring how fast the water flows can help determine whether the slide is safe for kids.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Momentum Flux: Refers to the quantity of motion carried by a fluid, which can be influenced by pressure and velocity.
-
Bernoulli’s Equation: Represents the conservation of energy principle for flowing fluids, connecting kinetic energy, potential energy, and fluid pressure.
-
Reynolds Transport Theorem: Establishes a relationship between the flow of mass, momentum, and energy through a volume over time.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: Calculate the velocity of fluid through a horizontal pipe using Bernoulli's equation.
-
Example 2: Apply momentum equations to a water jet striking a plate to find the angle of impact.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Pressure drops, velocity hops; a fluid's dance where energy stops.
📖 Fascinating Stories
-
Once there was a river, flowing fast, as it sped up, the pressure was cast; it learned to divert over rocks and lands, dancing through valleys, with energy at hand.
🧠 Other Memory Gems
-
For Bernoulli's equation, remember 'PEPV': Potential Energy, Pressure, Velocity.
🎯 Super Acronyms
Use 'BVP' for Bernoulli's Velocity Principle
- Fast flows mean low pressure.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Bernoulli's Equation
Definition:
A principle that describes the relationship between pressure, velocity, and elevation in fluid flow.
-
Term: Reynolds Transport Theorem
Definition:
A theorem used to derive the momentum equations for control volumes in fluid dynamics.
-
Term: Momentum Flux
Definition:
The rate of momentum transfer across a given area in a flowing fluid.