Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Linear Momentum Equations
Unlock Audio Lesson
Today, we will start our exploration of linear momentum equations. Can anyone remind me what momentum is?
Isn't it the product of mass and velocity?
Correct! Momentum is indeed mass times velocity. We will apply this to fluid flow using the Reynolds transport theorem. This theorem helps us relate the momentum of fluids moving through a control volume.
What is a control volume?
Great question! A control volume is a defined space through which fluid flows, allowing us to analyze the mass and momentum changes. Keep that in mind as we proceed.
Can you give us an example of where we might use this in real life?
Absolutely! We often use these principles in engineering applications like calculating forces on dams or aircraft wings. Let's move on to how we can quantify these concepts using equations.
To recap, momentum in fluid dynamics relates directly to our control volume and motion, and we'll simplify using the Reynolds transport theorem.
Applying Bernoulli's Principle
Unlock Audio Lesson
Now, let's delve into Bernoulli's equations, which are pivotal in our calculations. Can anyone tell me what Bernoulli's principle states?
It states that an increase in fluid speed occurs simultaneously with a decrease in pressure or potential energy.
Exactly! And we will use Bernoulli's equations to relate our momentum influx and outflux. In particular, we need to understand how to calculate these influxes.
Could you show us a formula for it?
Sure! The net momentum change we can work with can be represented as total mass flux times the velocity. As we look at steady flow, these terms allow us to derive our equations more clearly.
What if we want to calculate forces in different directions?
Excellent point! Separately calculating force components in both x and y directions helps us quantify resultant forces effectively. Let's recap the importance: Bernoulli helps relate speed and pressure while we track momentum!
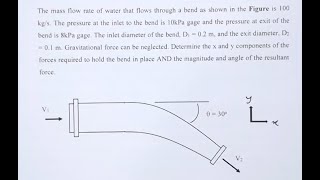
Example Calculations
Unlock Audio Lesson
Let's talk about our earlier example. We found a resultant force of 3.29 kilonewtons. Can anyone explain how we arrived at that value?
We calculated momentum outflux and inflow components and used them in the linear momentum equations!
Exactly! We broke down the problem using the mass flow rate and velocity. Now, how would we apply this in a scenario like a jet striking a plate?
We would first define the flow conditions, then apply Bernoulli's principle to predict pressures and velocities at different points.
That's right! Observing steady flow allows us to simplify our equations, leading to effective calculations. Recap this: Understanding practical examples reinforces our application of theoretical principles.
Venturimeter Example
Unlock Audio Lesson
Next, let's take a closer look at the venturimeter example. We know the pressure difference between two sections can help us determine fluid discharge. What do you think is key here?
We need to measure flow rates accurately!
Absolutely! By applying Bernoulli's equations and knowing our diameter measurements, we can derive the discharge coefficient effectively. What is the significance of this?
It provides a measure of how efficiently the venturimeter is operating!
Yes, well said! Understanding practical devices underlines the theory we learned: apply these principles in real-world situations! Who can summarize what we've done in this section?
We looked at linear momentum equations, applied Bernoulli's principles, and calculated resultant forces, including practical examples like the venturimeter.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section introduces linear momentum equations framed within the context of fluid dynamics. It explains how to apply the Reynolds transport theorem to derive equations for momentum influx and outflux, particularly in steady flow conditions. Several examples illustrate how to compute forces acting on a control volume, including applications of Bernoulli's principle.
Detailed
Linear Momentum Equations
In this section, we explore the application of linear momentum equations within fluid mechanics, primarily focusing on steady flows over a horizontal surface. We start with the Reynolds transport theorem as the foundational approach to simplifying linear momentum equations.
Key Concepts Covered:
- Reynolds Transport Theorem: This theorem allows us to analyze fluid motion and calculate the momentum for control volumes.
- Momentum Influx and Outflux: For a control volume with both mass influx and outflux, we represent momentum change through the momentum flux equations.
- Forces in Steady Flow: Under steady flow conditions, we demonstrate that certain terms may simplify, leading to clearer equations.
- Example Problems: The section includes multiple examples, showcasing how to compute resultant forces based on the momentum influx and outflux and applying Bernoulli's equations effectively in various scenarios.
The significance of understanding these concepts lies in their critical role in engineering fields involving fluid dynamics, enabling precise calculations of forces acting on surfaces due to moving fluids.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Linear Momentum Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
And here as you know it we have considered it is a horizontal surface. So z equal to z. That is what we cancelled out. And we are just substituting the mass conservation equation and the Bernoulli’s equations to compute what will be the Q value. So once I know the Q value to estimate whatever will be the force component will going to apply linear momentum equations.
Detailed Explanation
This chunk introduces the context for applying linear momentum equations in fluid mechanics. It emphasizes that in this analysis, the surface is horizontal, and heights (z values) are considered equal, allowing for simplifications. The next step involves substituting values related to mass conservation and Bernoulli’s equations to determine the flow rate (Q). This flow rate is essential for later calculations of forces using momentum equations.
Examples & Analogies
Imagine water flowing smoothly out of a garden hose held horizontally. Since the hose is at a constant elevation, we don’t need to worry about gravitational effects altering the water pressure above or below the hose. Instead, we focus on how the speed and amount of water (flow rate) affect how far that water shoots out.
Applying Reynolds Transport Theorem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Based on Reynolds transport theorems, we can write for linear momentum equations. We can write that the sum of the force is acting is equal to same path, change of... momentum outflux and this is what momentum influx components.
Detailed Explanation
This chunk focuses on the Reynolds transport theorem, which provides a way to relate changes in momentum within a control volume to the forces acting on that volume. It states that the sum of the forces acting on a fluid is equivalent to the change in momentum flux (both incoming and outgoing) across the control volume. This principle is foundational in fluid dynamics when analyzing flow through a system.
Examples & Analogies
Think of a crowded subway station. The people entering (influx) and leaving (outflux) create a net flow of people. If more people leave than enter, the crowd thins out. In fluid dynamics, similar logic applies: the forces acting on the fluid relate directly to how much momentum flows in and out of a defined space.
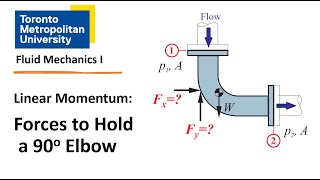
Calculating Forces in X and Y Directions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I apply in the x direction, we will get the sum of the force F x will be,... F will be 2.94 Newton.
Detailed Explanation
In this segment, the focus shifts to applying the momentum equations specifically in the horizontal (x) and vertical (y) directions. By calculating the momentum flux and applying the appropriate equations, the resultant forces in these directions are derived. For example, the calculation leads to an estimate of 2.94 Newtons in the x-direction. Understanding the breakdown along these axes is crucial for determining the overall effect of the fluid flow.
Examples & Analogies
Picture pushing a swing. If you push from the side (x-direction), it swings left and right. If you push from below (y-direction), it goes up and down. Similarly, fluid forces can be analyzed in different directions — understanding the contribution from each direction helps predict the swing's movement.
Finding Resultant Force
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
we can compute resultant force which will be... the resultant force is equal to 3.29 kilo Newton.
Detailed Explanation
This chunk discusses how to combine the computed forces from the x and y directions to get a resultant force. Here, the addition of 2.94 Newton (from the x-direction) and the force in the y-direction gives a final force of 3.29 kilo Newton, showing how both components work together to give an overall picture of the force exerted by the fluid.
Examples & Analogies
Consider pulling an object using ropes from two different angles; one from the left (x) and one from above (y). The total force acting on the object can be found using vector addition, just as the fluid forces combine to create a resultant force in our calculations.
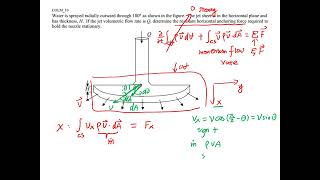
Example Problem Application
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In this case there is a horizontal jet of the flow with angle theta strike on a vertical plate... we can classify the flow, the flow classifications like the steady, incompressible and one dimensional flow even if it looks a two dimensional.
Detailed Explanation
In this example, a horizontal jet of fluid impacts a vertical plate. The flow is analyzed under assumptions of being steady and incompressible, which simplifies calculations. The momentum equations are applied to determine the angle (theta) of the jet's impact that keeps the system in equilibrium, emphasizing the practical application of the linear momentum equations discussed earlier.
Examples & Analogies
Think of a fireman's hose aiming water at a wall. The angle at which the water hits the wall is crucial for understanding how the water behaves. By adjusting the angle, the fireman can ensure that the water flows effectively without splashing back, analogous to using momentum equations to quantify the impact.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Reynolds Transport Theorem: This theorem allows us to analyze fluid motion and calculate the momentum for control volumes.
-
Momentum Influx and Outflux: For a control volume with both mass influx and outflux, we represent momentum change through the momentum flux equations.
-
Forces in Steady Flow: Under steady flow conditions, we demonstrate that certain terms may simplify, leading to clearer equations.
-
Example Problems: The section includes multiple examples, showcasing how to compute resultant forces based on the momentum influx and outflux and applying Bernoulli's equations effectively in various scenarios.
-
The significance of understanding these concepts lies in their critical role in engineering fields involving fluid dynamics, enabling precise calculations of forces acting on surfaces due to moving fluids.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Applying momentum equations to calculate forces acting on a control surface in a horizontal jet.
-
Using Bernoulli's equations to solve for velocity and pressure when measuring flow through a venturimeter.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Momentum flows high, like a river, don't let it die, mass times speed, that's the key, feel the motion, can't you see!
📖 Fascinating Stories
-
Imagine a racing car zooming down a track, its momentum builds as it speeds up, pushing through the air, showcasing how motion combines with mass. Each turn shows how momentum influences its path.
🧠 Other Memory Gems
-
To remember momentum: M for mass, O for object, V for velocity - it all adds up in motion!
🎯 Super Acronyms
MVP - Mass, Velocity, Pressure - key concepts in fluid dynamics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Linear Momentum
Definition:
The product of an object's mass and its velocity, representing the quantity of motion it possesses.
-
Term: Reynolds Transport Theorem
Definition:
A theorem that provides a framework for analyzing the dynamics of a fluid by relating changes in flow to rates of mass and momentum.
-
Term: Momentum Influx
Definition:
The rate at which momentum enters a defined control volume within a fluid system.
-
Term: Momentum Outflux
Definition:
The rate at which momentum exits a defined control volume within a fluid system.
-
Term: Bernoulli's Equation
Definition:
An equation that describes the conservation of energy in a flowing fluid, relating pressure, velocity, and height.