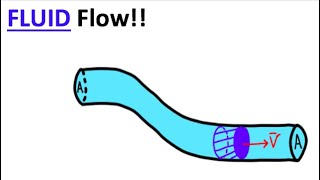
Momentum Influx and Outflux Components
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Momentum Influx and Outflux
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will be discussing momentum influx and outflux components. Can anyone tell me what momentum influx means?

Is it the amount of momentum entering a control volume?

Exactly! Momentum influx refers to the momentum flowing into a system. Now, how about momentum outflux? What does that imply?

I think it's the momentum that leaves the control volume.

Right again! Together, these components help us analyze fluid motion. Remember: Influx is the 'in' and outflux is the 'out.' We can summarize this with the acronym 'IO' for Influx-Outflux.
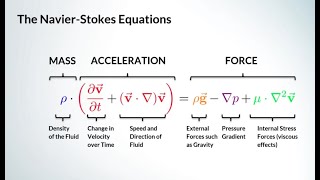
Applying the Reynolds Transport Theorem
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's talk about how we apply the Reynolds transport theorem. Can anyone describe its function?

It connects the change of momentum in a control volume to the flux across its boundaries?

Exactly! That’s a fantastic summary. We often say 'flux = flow' to help remember that momentum and mass are moving through boundaries. Can anyone provide an example of where we might apply this?

In analyzing a pipe system for water flow?

Correct! Great example. In this context, the Reynolds transport helps us to express the dynamics of the flow accurately.
Calculating Momentum Flux
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s dive into calculating momentum flux. If we think about fluid flowing through an area, how do we express momentum flux in terms of flow rate?

Isn't it related to density and velocity squared?

Very good! The momentum flux can be stated as the product of density and velocity squared, 'ρv²'. So, if we have momentum influx at area A1 and outflux at A2, can someone tell me the formula for that?

It’s like ΔMomentum = ρQ(A1) - ρQ(A2)?

Yes! Remember to include the directionality in your calculations. Momentum influx is positive flow towards the control volume, whereas outflux is negative. This gives us a complete picture of the forces at play.
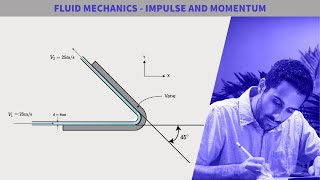
Real-Life Application: Example of Jet Impact on a Plate
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s apply what we've learned to a practical scenario: a water jet striking a vertical plate. How can we determine the force acting on the plate?

We can use Bernoulli’s equation to find velocity and then calculate the momentum change.

Exactly! Applying Bernoulli allows us to find velocity at the jet's impact point. 'Force = Mass Flux * Change in Velocity.' Can anyone summarize how we relate all this back to momentum influx and outflux?

By finding both influx when it strikes and outflux as it flows away, we can compute the total force exerted on the plate.

Spot on! This method illustrates practical engineering design considerations in fluid dynamics.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The content elaborates on how to apply Bernoulli's equation along with mass conservation principles to compute momentum influx and outflux in control volumes, emphasizing steady flow conditions. It introduces momentum flux components in the x and y directions and illustrates practical examples, thereby enhancing comprehension of the underlying concepts.
Detailed
In this section, we delve into the dynamics of momentum influx and outflux components essential for analyzing fluid mechanics. The discussion begins with the Reynolds transport theorem, which provides a framework for relating mass and momentum in flowing fluids. We apply linear momentum equations formulated from Bernoulli's principles, focusing on steady-state conditions where fluctuations in momentum are minimal. Key calculations involve determining mass and momentum fluxes at control surfaces, and we see how to compute resultant forces in different directions using these equations. Examples through jet impact on surfaces and venturimeters are introduced, facilitating a practical understanding of the concepts. Ultimately, the integration of these theories and equations assists in predicting fluid behavior and forces in various engineering applications.
Youtube Videos






Audio Book
Dive deep into the subject with an immersive audiobook experience.
Applying Linear Momentum Equations
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So based on Reynolds transport theorems, we can write for linear momentum equations. We can write that the sum of the force is acting is equal to same path, change of is equal to since it is a one inflow and one outflow, so we will have...
Detailed Explanation
In this step, we start by using the Reynolds transport theorem, which provides a framework to relate the rate of change of quantities to the flow into and out of a control volume. The theorem simplifies our linear momentum equations by stating that the net force acting on the system will equal the difference between the momentum entering and leaving the system. Because we are dealing with one inflow and one outflow, we can express this as the sum of forces equal to the total momentum influx minus the total momentum outflux.
Examples & Analogies
Think of this scenario like a busy highway. If we consider a section of the highway as our control volume, the cars entering and leaving represent the influx and outflux of momentum. Just like the total number of cars in that section will reflect how many enter versus how many leave, the total momentum entering the control volume must balance with that leaving.
Momentum Outflux and Influx Components
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So that is what is outflux, mass outflux. Sorry, this is what momentum outflux and this is what momentum influx components. And here we can assume it the velocity 1 and being a steady flow again, this part becomes zero, as it is a steady flow conditions.
Detailed Explanation
Next, we differentiate between the momentum influx and outflux components. The momentum influx relates to the mass and velocity of the fluid entering the control volume, while the outflux refers to the mass and velocity of the fluid leaving it. Since we assume a steady flow, any changes in momentum storage within the control volume are negligible, allowing us to focus solely on the momentum flowing in and out.
Examples & Analogies
Imagine a water tank with a steady inflow and outflow of water. If you fill the tank at the same rate as water is being drained, the water level remains constant. Similarly, when fluid flows in and out at a steady rate, we don't need to worry about changes within the tank, allowing us to simplify our calculations.
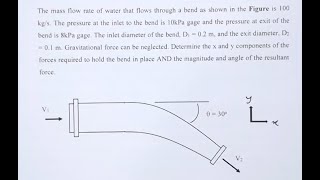
Calculating Force Components
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So we will play along the x directions to get it. If I apply in the x direction, we will get it the sum of the force F x will be...
Detailed Explanation
When calculating force components, we apply the linear momentum equations specifically along the x-direction. This involves computing the force based on the momentum flux components. The equation simplifies to show how the velocity, area, and density of the fluid relate to the overall force acting on the system. By substituting the values of mass flux and velocity into the force equation, we can determine the net force exerted in that direction.
Examples & Analogies
Think of pushing a swing. The force you exert pushes the swing forward (much like the momentum in our equations). If you push harder (increasing your force), the swing moves faster and reaches higher - similarly, changing fluid velocity influences the overall forces calculated here.
Resultant Force Calculation
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Similar way if I apply in the y directions, I am not doing for the y directions detail equations. We will also get it the...
Detailed Explanation
In calculating the resultant force, the process is similar for the y direction. Even though this section skips some detailed equations, we still recognize that each directional force contributes to the total force acting on the system. By summing up the x and y components, we can derive the overall or resultant force acting through the control volume.
Examples & Analogies
Consider the force needed to lift a box: you can think of it as needing to account for both the upward lift (y-direction) and any pushes or pulls from the side (x-direction). The overall effort you put in combines both of these efforts, just like we combine forces in our equation.
Example Calculation
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
As we know this F x and F y value then we can compute resultant force which will be...
Detailed Explanation
Here, we take our computed forces from the x and y directions and calculate the resultant force using vector addition. This is crucial because the resultant force gives us the total force acting on the control volume, enabling us to see the full impact of the momentum changes inside our system.
Examples & Analogies
This is like finding the overall direction and magnitude of wind walking through an open field. While the wind may be pushing from different sides at different strengths, when you combine those effects, you understand how it ultimately pushes you as you walk.
Key Concepts
-
Continuity Equation: The principle stating that mass flow rate remains constant throughout a fluid flow system in steady-state conditions.
-
Bernoulli's Equation: Describes the relationship between velocity, pressure, and elevation in fluid flows.
-
Momentum Transfer: The calculation or analysis of how momentum is conserved or transferred through different fluid flow scenarios.
Examples & Applications
Applying Bernoulli's equation in a venturimeter reduces pipe diameter allowing calculation of flow rate based on pressure difference.
Momentum change calculation by analyzing the forces on a surface where a jet impacts indicates the effectiveness of hydraulic designs.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In and out, momentum flows, through control surfaces, just as it shows.
Stories
Imagine a water jet hitting a wall, it pushes momentum in—a forceful call!
Memory Tools
Remember 'RMB' - Reynolds, Momentum, Bernoulli - for fluid dynamics in momentum discussions.
Acronyms
I.O. = Influx and Outflux for remembering momentum conceitos.
Flash Cards
Glossary
- Momentum Influx
The momentum entering a control volume.
- Momentum Outflux
The momentum leaving a control volume.
- Reynolds Transport Theorem
A mathematical framework that relates the rate of change of a property in a control volume to the flux of that property across the control surface.
- Momentum Flux
The rate at which momentum passes through a unit area.
- Bernoulli's Equation
A principle that describes the conservation of energy in a flowing fluid, relating pressure, velocity, and height.
Reference links
Supplementary resources to enhance your learning experience.
