Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Venturimeter
Unlock Audio Lesson
Today, we are discussing the venturimeter, a key device used to measure fluid flow rates efficiently. Can anyone tell me what a venturimeter is?
Is it a device that measures how much fluid flows through a pipe?
Exactly! It does this by using the principles of Bernoulli's equation, which connects pressure and velocity. So, why do we care about the pressure difference in a venturimeter?
Because it helps to calculate the flow rate?
Right again! The pressure difference tells us about the speed of the fluid. If we can measure that, we can find out the flow rate. Let's remember: 'PVE' - Pressure Velocity Equals flow rate!
Applying Bernoulli's Equation
Unlock Audio Lesson
Now, let's apply Bernoulli's equation to our venturimeter problem. Can someone remind me of what Bernoulli's equation states?
It's about the conservation of energy in fluid flow, right?
Exactly! It equates the total energy along a streamline. For our venturimeter, we can write it as P1 + (1/2)rho*v1^2 = P2 + (1/2)rho*v2^2. How does this help us?
We can solve for velocity differences at two points!
That's correct. This will help us find the theoretical flow rate. Remember, the smaller the area, the higher the velocity!
Calculating Discharge Coefficient
Unlock Audio Lesson
Now that we have derived the theoretical flow rate, let's think about how to compute the discharge coefficient, C_d. What do we need to find that value?
We need to compare it to the actual flow rate, right?
Absolutely! The formula is C_d = Q_actual / Q_theoretical. So, can anyone recall what our actual flow rate was?
It was 30 liters per second!
Correct! Now apply our formula to find C_d using the theoretical flow we calculated. This practice helps illustrate how closely theoretical estimations match real-world measurements.
Review and Key Points
Unlock Audio Lesson
Let’s recap what we've learned. We discussed the function of a venturimeter, applied Bernoulli's equation, and calculated the discharge coefficient. Can anyone summarize the significance of Bernoulli’s principle in fluid mechanics?
It helps us understand how pressure changes in fluid flow lead to velocity changes!
Exactly! Remember: Understanding how different properties relate helps predict behavior in various applications. Furthermore, pay attention to these equations while working on problems like this in the future.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we analyze a venturimeter problem involving fluid flow rates and pressure differences. By applying Bernoulli's equation and concepts of fluid momentum, we derive the discharge coefficient and address the relationships between flow areas and pressures.
Detailed
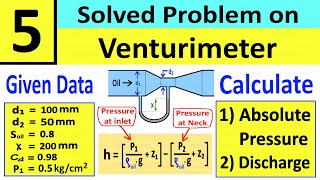
In this section, we explore a venturimeter installation that consists of a pipeline where the diameter changes from 15 centimeters to 7.5 centimeters. Given a flow rate of 30 liters per second and a measured pressure difference of 2.45 meters of water head, we aim to find the discharge coefficient of the venturimeter (C_d). The analysis involves applying Bernoulli's equation that links flow velocities, areas, and pressure differences, under the assumption of steady, incompressible flow. Furthermore, we derive the relationship between theoretical and actual flow to compute the discharge coefficient based on the given values. This problem illustrates fundamental fluid mechanics principles, including the use of Bernoulli's equation to correlate flow rate with kinematic and dynamic aspects of fluid movement.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to the Venturimeter
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The example 5, which is a very simple problems on venturimeter as given in this figure. That there is a venturimeter with having the diameter of 15 centimeters is reduced to the 7.5 centimeters, which is installed on a horizontal pipeline. And the rate of the fluid passing through this, the Q is equal to 30 liters per seconds, Q equal to 30 liter per second.
Detailed Explanation
In this example, we are discussing a device called a venturimeter, which is used to measure the flow rate of fluids in pipes. The venturimeter works by having a pipe with varying diameters; in this case, the diameter decreases from 15 centimeters to 7.5 centimeters. When fluid flows through this section of the pipe, it speeds up due to the decrease in diameter, which leads to a change in pressure. We know that the fluid passes through this venturimeter at a rate of 30 liters per second.
Examples & Analogies
Think of a garden hose. When you put your thumb over the end of it slightly, the water speeds up and shoots out further. This is similar to how a venturimeter functions—when the diameter of the pipe narrows, the fluid speeds up resulting in a measurable decrease in pressure.
Understanding Pressure Difference
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
And the pressure difference between this throat and enlarged part. That is the pressure difference between P 1 and P 2 as we can find out the pressure difference as given here the pressure difference is equal to 2.45 meters in terms of the water head, in terms of the water head.
Detailed Explanation
The pressure difference is crucial for determining the discharge coefficient of the venturimeter. Here, P1 refers to the pressure at the wider section of the pipe before the fluid passes through the narrower throat, while P2 is the pressure at the throat itself. In our example, this pressure difference is provided as equivalent to a height of 2.45 meters of water.
Examples & Analogies
Imagine filling a U-shaped tube with water and noticing the difference in water levels when you push water through one side. The difference in height represents the pressure difference and is similar to what happens in a venturimeter.
Applying Bernoulli’s Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This case, we can take a the centrally flow part which will be a streamlined part this. And along the streamlines, we can apply the Bernoulli’s equations to find out what could be the Q theoretical value.
Detailed Explanation
In fluid dynamics, Bernoulli’s equation helps us relate the pressure, velocity, and height of a flowing fluid. In our case, we apply it along the streamline of the venturimeter. By doing so, we can calculate the theoretical flow rate (Q) based on the cross-sectional areas of the pipe before and after the throat and the measured pressure difference.
Examples & Analogies
Consider driving a car: the faster you go (higher velocity), the more you feel the wind resistance (lower pressure inside the car). Similarly, in a venturimeter, as fluid speeds up in the narrow section, it creates a pressure drop that can be calculated using Bernoulli’s equation.
Calculating Discharge Coefficient
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I apply this Bernoulli’s equations, Bernoulli’s equations as we apply on along this the streamlines, it can easily we can write it the same form. Since in this case, whatever the Q amount of the flow comes it, the Q will be the A V, A V. And since it is, we know the pressure difference between 1 and 2 points, that is the reasons we can easily compute this pressure difference between two point as it is measure it.
Detailed Explanation
By applying Bernoulli’s equation and knowing the cross-sectional areas at points 1 and 2, we can derive a formula for the flow rate. Given the known values for pressure difference and pipe dimensions, we can determine the theoretical discharge (Q theoretical) of the venturimeter. The actual discharge can then be used to compute the discharge coefficient (C_d).
Examples & Analogies
Think of it this way: if you're trying to optimize the output of a juice extractor, you would measure how much juice it should ideally produce (theoretical) based on the fruit size and type, then compare it to what you actually get (actual) to understand its efficiency (discharge coefficient).
Final Calculation of C_d
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So the basic idea is here to apply the Bernoulli’s equations along this streamlines. If I apply this Bernoulli’s equations, you know this value of A A value as the diameter is given to us 2.45, 2g all the value is 1 2 given to us. So we can compute the C d value which comes out to be 0.95 for this case.
Detailed Explanation
After substituting all known values into our equation derived from Bernoulli’s, we can isolate the variable for C_d (discharge coefficient) to find that it equals 0.95. This number helps us understand how efficient this venturimeter is in moving fluid through the system compared to its theoretical flow rate.
Examples & Analogies
If we think of the discharge coefficient as a performance rating, a C_d of 0.95 means this venturimeter is quite effective, like having a highly efficient appliance that uses almost all of its input energy to produce output.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Venturimeter: A device measuring flow rate based on pressure changes.
-
Bernoulli's Equation: Relates pressure and velocity in fluid dynamics.
-
Flow Rate: A key measurement in fluid systems, usually in liters per second.
-
Discharge Coefficient: Shows efficiency of fluid flow through a device.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
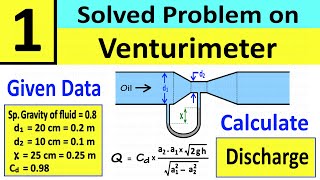
Example 1: In a venturimeter setup, if the entrance diameter is 15 cm and the throat diameter is 7.5 cm, using Bernoulli's equation can lead to a theoretical flow rate calculation if pressure differences are known.
-
Example 2: If the measured pressure difference in a venturimeter is 2.45 meters of water and the actual flow rate is 30 liters per second, you can compute the discharge coefficient to assess device performance.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a venturimeter's flow, pressure drops and speed will grow.
📖 Fascinating Stories
-
A curious engineer places a venturimeter in a pipe and wonders how fluid speeds up when it gets constricted, discovering the magic of natural pressure changes.
🧠 Other Memory Gems
-
Remember: 'PV = Q', where P is pressure, V is velocity, and Q is flow rate.
🎯 Super Acronyms
C_d = Q_a / Q_t, where C_d is discharge coefficient, Q_a is actual flow rate, and Q_t is theoretical.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Venturimeter
Definition:
A device used to measure the flow rate of a fluid through a pipe by observing changes in pressure.
-
Term: Bernoulli's Equation
Definition:
An equation that relates the pressure, velocity, and elevation of a fluid along a streamline.
-
Term: Discharge Coefficient (C_d)
Definition:
The ratio of the actual flow rate to the theoretical flow rate in a system.
-
Term: Flow Rate (Q)
Definition:
The volume of fluid that passes through a surface per unit time, commonly measured in liters per second.
-
Term: Pressure Difference
Definition:
The difference in fluid pressure between two points, critical for calculating flow rates in venturimeters.