Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Linear Momentum Equations
Unlock Audio Lesson
Today, we will explore linear momentum equations in control volume analysis. Let's start by defining momentum in the context of fluid flow. Can anyone tell me what momentum is?
Isn't momentum the mass of an object multiplied by its velocity?
Exactly! And in fluid mechanics, we often look at systems where mass is flowing, so we will apply linear momentum equations to control volumes. Does anyone remember what the Reynolds transport theorem helps us with?
It helps in converting the time rate of change of momentum for a system to that for a control volume?
Correct! This theorem is central to our understanding. Remember, we can model fluid mass flow using equations derived from this theorem, and simplify them according to our system's conditions.
So we can set up equations based on inflow and outflow?
That's right! We'll specifically look at momentum influx and outflux, which help us calculate the forces acting on the fluid. Let's summarize today's focus: understanding linear momentum, applying the Reynolds transport theorem, and setting up control volume equations.
Application of Bernoulli’s Equation and Momentum Analysis
Unlock Audio Lesson
Now, let’s consider the application of Bernoulli's equation in analyzing fluid flow through a horizontal jet. What can we remember about Bernoulli's principles?
It relates pressure, velocity, and elevation in a flowing fluid, right?
Exactly! By applying Bernoulli’s equation between two points in our flow, we can derive important relationships. Can anyone explain how we can set this up?
We can visualize the streamline and apply Bernoulli's equation from one point to another?
Yes! As we analyze forces, we'll compute momentum flux from these points and how changes in pressure relate to velocity. The relationship involving velocity areas aids us in calculating force components. We need to keep track of units and conditions, like steady flow.
How do we calculate the resulting forces?
Good question! By determining the changes in momentum flux from our equations, we can assess both x and y components and find the resultant force. Remember, let's summarize key points for easier recall.
Example Problems and Real-World Applications
Unlock Audio Lesson
To solidify our learning, let’s work through an example problem involving a horizontal jet of flow striking a plate. What critical factors do we need to consider in this setup?
The flow rate and pressure differential, right?
Exactly! As we analyze this, we can apply momentum equations for both inflow and outflow conditions. Based on these forces acting, what do you think our next steps would be?
We should set up the equations to solve for the angle at which the jet impacts the plate?
Yes, great thinking! We’ll need to express our forces in terms of the given parameters, deducing the resultant impact angle after substituting the known values accordingly.
So we ultimately compute theta by observing the balance in forces?
Exactly! With this example, you will see the power of linear momentum equations in practical applications. Remember to continue practicing these setups and solving the resulting equations. Now, let's summarize key learning points.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the significance of linear momentum equations in fluid dynamics is explored, focusing on how they can be applied to control volumes using Reynolds transport theorem. Key examples illustrate how to compute forces acting on fluid flows through jets and pressure differentials, reinforcing the concepts through practical applications.
Detailed
Linear Momentum Equations for Control Volume
This section provides a thorough exploration of linear momentum equations as applied to control volumes in fluid mechanics. The main focus is on how to utilize the Reynolds transport theorem to derive and simplify these equations and investigate their practical implications.
Initially, the concept addresses the need for evaluating flow-related forces using mass conservation and Bernoulli’s principles. The section further elaborates on establishing momentum influx and outflux in a steady flow regime, resulting in the determination of force components acting in both the x and y directions.
Key examples, such as the behavior of a horizontal jet striking a plate and computations involving venturimeter flow, provide concrete applications of theoretical principles, facilitating deeper understanding of how to derive angular momentum values, calculate pressures, and analyze fluid flow characteristics effectively.
By the end of the section, readers should grasp the essential process of applying linear momentum equations and how these can lead to solving real-world fluid dynamics problems effectively.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Linear Momentum Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
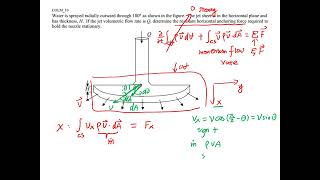
And here as you know it we have considered it is a horizontal surface. So z equal to z1. That is what we cancelled out. And we are just substituting the mass conservation equation and the Bernoulli’s equations to compute what will be the Q value. So once I know the Q value to estimate whatever will be the force component will going to apply linear momentum equations.
Detailed Explanation
In this section, we begin by considering a horizontal surface for our control volume analysis, simplifying our calculations as the vertical component is dismissed (z = z1). We replace the mass conservation equation and Bernoulli’s equations, which are fundamental in fluid mechanics, to find the discharge rate Q. Knowing the flow rate is critical to estimating force components using linear momentum equations.
Examples & Analogies
Think of measuring water flowing from a hose. Conservation of mass ensures that the amount of water flowing into a segment of the hose equals the amount flowing out, just as we apply mass conservation to understand how it affects linear momentum in our calculations.
Application of Linear Momentum Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We are going to apply linear momentum equations. Let us apply the linear momentum equations for these problems. And always I encourage that, please start applying the Reynolds transport theorems, simplify the Reynolds transport theorems from linear, basic linear momentum equations to the simplification functions.
Detailed Explanation
We now apply linear momentum equations to analyze our control volume effectively. It's important to use Reynolds transport theorem, which connects the information at the system boundaries to the control volume, providing a framework to simplify the analysis of momentum, especially in various flow conditions.
Examples & Analogies
Imagine trying to track a crowd leaving a concert through various exits. The Reynolds transport theorem helps us determine how many people leave through each exit by looking at the crowd's flow as a whole, similar to how we apply physics to momentum.
Forces and Momentum Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
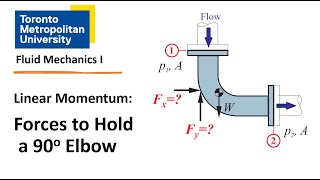
So based on Reynolds transport theorems, we can write for linear momentum equations. We can write that the sum of the force is acting is equal to sum of the momentum outflux minus sum of the momentum influx.
Detailed Explanation
Using the Reynolds transport theorem, we establish that the total forces acting on the control volume equal the difference between momentum flowing out and momentum flowing in. This fundamental principle helps us determine how the various forces are balanced within the flow, ensuring that we account for all inputs and outputs.
Examples & Analogies
Consider a bathtub: the water coming in through the faucet equals the water flowing out the drain when it’s full. Likewise, the balance of momentum inflow and outflow defines the behavior of our fluid in the control volume.
Calculating Momentum Flux
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
And here we can assume it the flow is steady again, this part becomes zero as it is a steady flow condition. So you just have to compute the momentum flux, influx and the outflow. That what the net momentum outflux what is happening through this control surface.
Detailed Explanation
In fluid dynamics, a steady flow condition implies that the flow properties at a point do not change over time. Under this assumption, we can ignore certain dynamic changes and focus solely on calculating the momentum flux at the inlet and outlet of our control volume, which is essential to understanding how the flow's momentum impacts the overall system.
Examples & Analogies
Think of a constant-flow fountain: the water level remains the same because the amount of water flowing in matches the amount flowing out. This steady-state flow indicates we can measure its output without needing to adjust for changes over time.
Force Components in X and Y Directions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
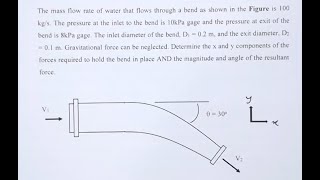
We will play along the x directions to get it. If I apply in the x direction, we will get it the sum of the force F_x will be... (equations) ... If I substitute these values, then we will get, F will be 2.94 Newton.
Detailed Explanation
By analyzing the forces in different directions, we can isolate the effects of momentum in both the x and y components. This allows us to compute the net forces acting on our control volume from each of these directions. For instance, using momentum flux values, we find that the force in the x-direction computes to 2.94 Newtons, which represents how much force is exerted due to the momentum of the fluid flowing through the control volume.
Examples & Analogies
Visualize a car moving down a gentle hill. When assessing its motion, you can look at forces along the incline (x direction) and perpendicular to it (y direction). By breaking it down this way, you can better understand its speed and direction, much like analyzing fluid forces.
Resultant Force Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Similar way if I apply in the y directions... (equations) ... we will also get... (result) ... So as we know this F_x and F_y value then we can compute resultant force which will be 3.29 kilo Newton.
Detailed Explanation
After calculating forces in both the x and y directions, we can find the resultant force, which combines these two components to give a comprehensive picture of the total force acting on the control volume. Here, we arrive at a resultant force of 3.29 kilo Newton, illustrating how fluid momentum influences system dynamics.
Examples & Analogies
If you push a box diagonally across a floor, you’re applying forces in both forward and sideways directions. By calculating these forces, you can determine the box’s overall movement, paralleling how we assess the fluid's net impact.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Momentum: The product of mass and velocity, crucial in analyzing force in fluid flows.
-
Control Volumes: Defined regions from which to analyze fluid motion and force interactions.
-
Reynolds Transport Theorem: A fundamental theorem connecting system dynamics and control volume analysis.
-
Bernoulli's Equation: Relates the pressure, velocity, and height of fluid dynamics to understand energy conservation.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Horizontal jet striking a plate, computing impact angle using flow rates and momentum equations.
-
Using a venturimeter to relate pressure difference with fluid flow rates, applying Bernoulli's principles.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluid's dance, motion holds sway, Momentum moves, keep friction at bay.
📖 Fascinating Stories
-
Imagine a river flowing fast, its mass and speed make waves that last. To track the force on the shore, we apply our equations—now we soar!
🧠 Other Memory Gems
-
Remember PE + KE = constant energy in Bernoulli's equation—a fluid's delight!
🎯 Super Acronyms
MVP
- Momentum gives Velocity's Power in our fluid flow analysis!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Control Volume
Definition:
A defined region in space through which fluid flows, allowing analysis of fluid behavior and forces.
-
Term: Reynolds Transport Theorem
Definition:
A theorem that relates the change of a quantity (like momentum) in a system to the flow of that quantity across control volume boundaries.
-
Term: Momentum Flux
Definition:
The rate of flow of momentum through a unit area, vital for calculating forces in fluid motions.
-
Term: Bernoulli’s Equation
Definition:
An equation that describes the conservation of energy in flowing liquids, relating pressure, velocity, and elevation.