Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Reynolds Transport Theorems
Unlock Audio Lesson
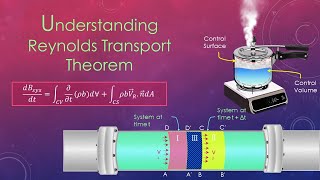
Today, we are going to explore the Reynolds Transport Theorems, or RTT, which allows us to relate the behavior of fluids within a control volume to those flowing across its boundaries.
Why is it important to understand these theorems?
Great question! Understanding RTT helps us conserve mass and momentum in fluid flows. It’s a backbone for many hydraulic and engineering applications. For instance, it allows us to calculate forces in fluid everywhere.
Can you give us a scenario where this applies?
Absolutely! For example, when analyzing the flow around a pipe, RTT helps us to track the change in momentum due to inflow and outflow.
Applying Linear Momentum Equations
Unlock Audio Lesson
Let's apply what we learned about RTT to derive linear momentum equations. Can someone start by summarizing the key flows of momentum?
The momentum of a fluid depends on both the mass and the velocity of the fluid, right?
Exactly! So when analyzing momentum, we examine both inflow and outflow in a control volume.
How do we simplify equations under steady flow conditions?
In steady flow, we can state that mass and momentum don't change within the control volume, allowing us to focus purely on incoming and outgoing fluxes.
Using Bernoulli's Equation
Unlock Audio Lesson
Now, let's integrate Bernoulli’s equation into our study. Who can explain why Bernoulli’s equation is relevant in this context?
It helps us understand how pressure, velocity, and elevation are related in fluid flows, particularly when the flow is steady and incompressible.
Exactly! Keeping these relationships in mind allows us to calculate flow velocities and pressure differences at different points in a flow system.
Can we see an example of this?
Sure, let's look at a horizontal jet striking a plate, where we can apply Bernoulli’s equation to analyze theta behavior.
Real-World Applications and Example Problems
Unlock Audio Lesson
Let’s apply our understanding with a practical problem. Who remembers the setup for a venturimeter?
It has a larger diameter expanding into a smaller one to measure fluid flow rates.
Correct! Let's calculate the discharge coefficient using both the theoretical calculations and observed data.
What are the key variables we’ll need?
We need the flow rates, pressure differences, and cross-sectional areas at different points along the venturimeter.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section highlights how Reynolds Transport Theorems can be derived and simplified to compute force components using linear momentum equations, particularly in steady flow conditions. It includes examples demonstrating how to apply Bernoulli's equation within control volumes to analyze fluid flow behavior.
Detailed
Detailed Summary
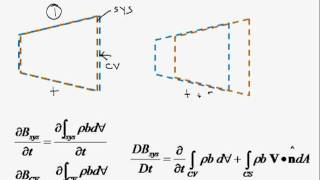
In this section, we delve into the Reynolds Transport Theorem (RTT), a fundamental principle in fluid dynamics that relates the rate of change of a quantity in a control volume to the net flux through its boundaries. The focus is particularly on linear momentum equations, which are crucial for understanding force components acting on fluid systems. Starting with a simple horizontal surface assumption, we explore key concepts like mass conservation and Bernoulli's equations to compute discharge (Q) values.
The section emphasizes that for steady flow conditions, we can simplify the RTT to derive momentum flux values for both inflow and outflow. Using these concepts, we learn how to calculate resultant forces acting in both x and y directions, linking them back to the underlying principles of mass and momentum conservation.
The provided examples, including a case involving a horizontal jet striking a vertical plate and a venturimeter problem, exemplify practical applications of these theorems, guiding us through the necessary calculations and logical deductions needed to solve fluid dynamics problems. By understanding these principles, engineers can accurately predict fluid behavior and design efficient systems.
Youtube Videos
![Get to know Reynolds Transport Theorem - part II [Fluid Mechanics]](https://img.youtube.com/vi/AGDXYZ2pdTA/mqdefault.jpg)
![Get to know Reynolds Transport Theorem - part I [Fluid Mechanics]](https://img.youtube.com/vi/BwOnHIsgK_Q/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Application of Linear Momentum Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
And we are just substituting the mass conservation equation and the Bernoulli’s equations to compute what will be the Q value. So once I know the Q value to estimate whatever will be the force component will going to apply linear momentum equations.
Detailed Explanation
In fluid mechanics, we often want to find out how various forces act on a fluid as it moves. Here, we're beginning to apply linear momentum equations after understanding the flow rate (Q value) through mass conservation and Bernoulli's principle. The Q value represents the volume of fluid passing through a specific area in a given time, and knowing this helps us evaluate the forces exerted by the fluid on surrounding structures.
Examples & Analogies
Imagine a garden hose: when you turn on the water, it flows out of the nozzle at a certain rate (Q value). If you wanted to understand how that water affects plants or structures nearby (like pushing against a wall), you would use linear momentum equations to calculate those forces based on the flow rate.
Reynolds Transport Theorems for Linear Momentum
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
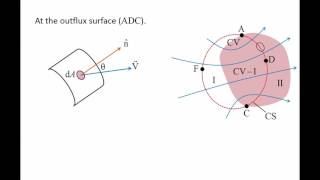
So based on Reynolds transport theorems, we can write for linear momentum equations. We can write that the sum of the force is acting is equal to same path, change of is equal to since it is a one inflow and one outflow, so we will have, momentum outflux and this is what momentum influx components.
Detailed Explanation
Reynolds Transport Theorem describes how the momentum of a fluid changes within a control volume. It states that the sum of the forces acting on this volume equals the change in momentum. If we have one inlet (inflow) and one outlet (outflow) of fluid, we need to account for the momentum that enters and the momentum that exits to evaluate the net effect, leading to an understanding of how forces are distributed in the fluid.
Examples & Analogies
Think of a busy highway: cars entering (inflow) and leaving (outflow) create traffic patterns. The total 'momentum' can be thought of as the number of cars multiplied by their speed. If more cars enter than leave, traffic jams might occur (net force acting), while the opposite reduces congestion.
Steady Flow Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
And here we can assume it the momentum conditions become zero, as it is a steady flow conditions.
Detailed Explanation
In steady flow conditions, the liquid's velocity remains constant at any point over time. This means that the flow properties (like velocity, pressure, etc.) do not change as time progresses. In such situations, for the analysis of forces, we can simplify our equations as we don't need to consider changing conditions.
Examples & Analogies
Imagine water flowing steadily from a faucet: the flow rate is consistent, and it splashes out in a smooth stream without interruption. This predictability simplifies calculations related to how the water impacts surfaces.
Calculating Momentum Flux and Resultant Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So we will play along the x directions to get it. If I apply in the x direction, we will get it the sum of the force F x will be, momentum flux components will come it. That what will be the minus rho Q square by A 1.
Detailed Explanation
When applying forces in the x-direction, we derive formulas based on the characteristics of the fluid (like density, denoted rho) and the flow parameters (Q and A1). Momentum flux is essentially the quantity of momentum passing through an area per unit of time. This allows us to compute the forces in that direction caused by the fluid flow.
Examples & Analogies
Consider a river pushing against a dam. The force exerted by the flowing water can be likened to momentum flux. By knowing how fast the river flows and its width, we can calculate how hard it pushes against the dam, just like how we compute forces using fluid density and flow rates.
Resultant Force Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So we will also get it the F y value, then we can compute resultant force which will be... Thus, the value comes out to be 3.29 kilo Newton.
Detailed Explanation
After obtaining both the x and y force components from the momentum calculations, we can determine the resultant force using vector addition. The final computation gives us a precise amount of force acting on a surface, which in this scenario is a water jet impact quantified at 3.29 kilo Newton.
Examples & Analogies
Imagine two people pushing a heavy box from different angles. To find out how hard they're pushing together, we would consider the direction and force of each push (the x and y components) combining these helps us see the total effort applied to move the box.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Reynolds Transport Theorems: Link fluid behavior within control volumes to boundary flows.
-
Momentum Equation: Fundamental to relating fluid motion to forces.
-
Bernoulli's Principle: Essential for linking velocity, pressure, and elevation energy conservation within flows.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of applying Bernoulli's equation to a horizontal jet hitting a plate to find the angle of impact.
-
Calculating discharge coefficient using venturimeter setup data for fluid flow rates.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a control volume, mass we save, / Its changes in flux we always crave.
📖 Fascinating Stories
-
Imagine a stream flowing into a pond. The water level rises as more flows in. Here, you see RTT in action as the inflow impacts the level inside—just like analyzing momentum in fluids!
🧠 Other Memory Gems
-
MVP: Mass, Velocity, Pressure - key factors in RTT applications.
🎯 Super Acronyms
RTT
- Remember **R**elation of **T**ime and **T**ransport.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Reynolds Transport Theorem
Definition:
A theorem that relates the time rate of change of a quantity to the flux of that quantity across the boundary of a control volume.
-
Term: Linear Momentum Equation
Definition:
An equation that describes the motion of a fluid in terms of its mass and velocity, considering forces acting on it.
-
Term: Bernoulli's Equation
Definition:
An equation that describes the conservation of energy in flowing fluids, relating pressure, velocity, and elevation.
-
Term: Control Volume
Definition:
A defined volume in fluid dynamics through which fluid may flow, used for analysis.
-
Term: Momentum Flux
Definition:
The rate of flow of momentum through a unit area.