Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Triaxial Tests
Unlock Audio Lesson
Today, we're diving into triaxial tests, starting with the Consolidated-Drained test. Who can tell me what a triaxial test is?
Isn't it a test we use to assess soil strength?
Exactly! Triaxial tests help us understand how soils behave under different stress conditions. Let's discuss the setup. Can anyone describe how the soil specimen is prepared?
The soil is placed in a rubber membrane inside a chamber, right?
Correct! That chamber helps apply confining pressure. Remember, we can adjust the pressure while allowing drainage during our test.
Understanding Principal Stresses
Unlock Audio Lesson
Now, let's talk about principal stresses. What are σ1, σ3, and how do they relate?
σ1 is the major principal stress and σ3 is the minor principal stress, right?
Absolutely! In a failure state, σ1 equals the total stress at failure. Why do you think understanding these stresses is crucial?
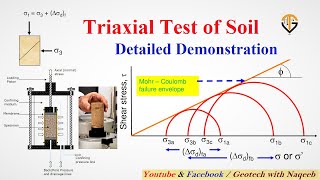
It helps us plot the Mohr’s circle and determine the shear strength parameters!
Exactly! The Mohr-Coulomb failure envelope helps us predict how the soil will perform under loads.
Mohr-Coulomb Failure Criterion
Unlock Audio Lesson
Let’s get into the Mohr-Coulomb failure criterion. What can you tell me about it?
It’s used to determine the shear strength of soil based on c and φ values.
Right! In a CD test, we use relationships involving cohesion c and internal friction φ to derive our failure envelope. What equation would you use?
s = c + σ tan(φ) is the one linking stress to shear strength!
Well done! Remember, these equations help engineers make crucial decisions in construction projects.
Applications of the CD Test
Unlock Audio Lesson
Lastly, why do we conduct these tests in real-world scenarios?
To ensure soil stability for constructions like bridges and buildings.
Absolutely! Ensuring safety in engineering design is our ultimate goal. Can anyone give an example of how this test impacts design?
It helps in determining how deep foundations need to be for different soil types!
Perfect! This understanding helps mitigate risks and ensures successful engineering projects.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The consolidated-drained test (CD test) assesses the mechanical properties of clayey soils by subjecting a soil specimen to controlled conditions in a triaxial chamber. It is a key method for determining shear strength parameters such as cohesion and internal friction angle, allowing engineers to evaluate soil stability and design accordingly.
Detailed
Detailed Summary
The Consolidated-Drained (CD) test is a fundamental procedure in geotechnical engineering for understanding the behavior of saturated soils, particularly clay. In a triaxial test setup, a soil specimen is confined within a rubber membrane and subjected to an isotropic confining pressure (σ3). The test can adjust the confining pressure to analyze the soil under various stress conditions, following the principles of effective stress.
In the CD test, drainage from the specimen is permitted during the testing process, allowing pore water pressures to dissipate, which leads to a more representative measure of soil strength in natural conditions. Upon failure, the relationships among the principal stresses are established, helping to develop the Mohr-Coulomb failure envelope. Importantly, the CD test provides crucial parameters like cohesion (c) and the angle of internal friction (φ), which are vital for evaluating soil stability, especially in projects related to constructing foundations, embankments, and other earth structures.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Consolidated-Drained Tests
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Triaxial tests can be conducted on sands and clays. Essentially, it consists of placing a soil specimen confined by a rubber membrane in a Lucite chamber. An all-round confining pressure (σ3) is applied to the specimen by means of the chamber fluid. Drainage from the specimen can be allowed or stopped, depending on the test condition.
Detailed Explanation
A consolidated-drained (CD) test is a type of triaxial test where a soil specimen is contained within a chamber. This chamber is designed to apply uniform pressure around the specimen (denoted as σ3). The key aspect is that the drainage is permitted, which means any pore water generated within the soil can flow out during loading. This is important as it helps in measuring the effective stress in the soil, allowing for accurate evaluation of its strength properties.
Examples & Analogies
Think of the CD test as a sponge that you place in a container filled with water. As you squeeze the sponge (applying pressure), the water can drain out, mimicking how water drains from saturated soil when pressure is applied. This drainage affects how strong the sponge (or soil) becomes during the squeezing process.
Application of All-round Confining Pressure (σ3)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
An all-round confining pressure (σ3) is applied to the specimen by means of the chamber fluid (generally water or glycerin). An added stress (Δσ) can also be applied to the specimen in the axial direction to cause failure (Δσ=Δσf at failure).
Detailed Explanation
In a CD test, the confining pressure (σ3) is essential because it simulates the pressures that soil experiences when buried under layers of material. Along with this, an additional stress (Δσ) is applied in the vertical direction which ultimately leads to soil failure. The relationship Δσ=Δσf indicates that when we want to fail the soil, the applied stress must equal the stress at failure (Δσf). This helps in understanding how different soil types react under pressure.
Examples & Analogies
Imagine stacking books on a table, where each book represents a layer of soil. The weight of the books above (confining pressure) creates pressure on the book at the bottom. If you suddenly add a heavy object on top (additional stress), the bottom book could crack or break (soil failure). This illustrates how increasing pressures can lead to structural failure in soils.
Plotting Mohr’s Circles and Failure Envelopes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The shear strength parameters (c and ϕ) can now be determined by plotting Mohr’s circle at failure, as shown in the figure, and drawing a common tangent to the Mohr’s circles.
Detailed Explanation
During the test, we can derive important shear strength parameters known as cohesion (c) and angle of internal friction (ϕ) using graphical methods. By plotting Mohr's circle for stress states before and after failure, we can visualize how the soil behaves. A tangent drawn to these circles establishes what is known as the Mohr-Coulomb failure envelope – a graphical representation that helps predict failure conditions for soil.
Examples & Analogies
Consider drawing a curve to connect points where a ball rolls down different slopes. The slope represents the soil's ability to hold together under stress. The more curves you draw, the better you can predict how the ball (or in this case, the soil) will behave under various pressures, similar to how Mohr's circles help us visualize soil strength and stability.
Determining Effective and Total Stresses
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
At failure, the relationships between major principal stresses are defined as Major Principal effective stress =σ3=Δσf=σ1 and Minor Principal effective stress =σ3=Δσ′3.
Detailed Explanation
Understanding effective stress is crucial in soil mechanics. It defines how much stress the soil skeleton (actual structure of the soil) can bear after subtracting pore water pressures. At failure, the major principal effective stress is given, showing the relationship between the confining pressure, added stress at failure, and the total stress acting on the soil. It outlines how these stresses work together to influence soil behavior under load.
Examples & Analogies
Imagine you are standing on a sponge that is filled with water. The weight of your body exerts pressure onto the sponge, but some of that pressure is taken up by the water inside the sponge (pore pressure). The effective stress which acts to compress or solidify the sponge is what remains after considering how much pressure the water is taking. Thus, knowing the effective stress helps us understand how soils behave under loads.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Consolidated-Drained Test: A triaxial test that allows drainage; used to determine effective stress parameters.
-
Mohr’s Circle: A graphical representation used to analyze stress conditions in materials and define failure.
-
Pore Water Pressure: The pressure of water within the soil pores, significantly affecting soil behavior.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of a CD test on clay: engineers applying increasing confining pressures to monitor soil strength.
-
Using strength parameters derived from a CD test to predict the stability of a proposed highway embankment.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a chamber, soil's confined, with pressures well-defined. Shear strength measures in the fray, help in stability every day.
📖 Fascinating Stories
-
Imagine a team of engineers in a lab, with a soil specimen in a triaxial chamber. They carefully apply pressure, all the while checking the pore water pressure. As they reach failure, they note their results – vital information for stable designs ahead!
🧠 Other Memory Gems
-
C-D tells the p-lay: Consolidated and drained, measure soil's way!
🎯 Super Acronyms
C-D test
- Cohesion (c)
- Drainage (D)
- test of strength in complex clay.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Effective Stress
Definition:
The stress carried by the soil skeleton, calculated as total stress minus pore water pressure.
-
Term: MohrCoulomb Failure Envelope
Definition:
A graphical representation of the relationship between shear stress and normal stress at failure conditions.
-
Term: Confining Pressure (σ3)
Definition:
The pressure applied uniformly in all directions around a soil sample.
-
Term: Principal Stress
Definition:
Stresses acting on a material in mutually perpendicular directions, typically denoted as σ1, σ2, and σ3.