Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the UU Test
Unlock Audio Lesson
Today, we are going to learn about the Unconsolidated-undrained test, commonly known as the UU test. Can anyone briefly describe what they think happens in this test?
I think it tests how soil behaves when we apply pressure without draining it, right?
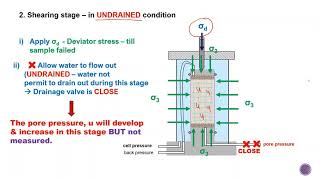
Exactly! The UU test evaluates the shear strength of saturated soils without allowing any drainage. So, we keep the soil in a confined chamber with water. What do you think happens to the porewater pressure in such a condition?
I guess it increases due to the applied pressure?
Correct! This increased pore water pressure influences the strength we measure. That's a key factor in why we conduct the UU test. Remember, UAQ: Unconsolidated and Undrained, leads to Pore Pressure changes.
Understanding Effective and Total Stress
Unlock Audio Lesson
Let’s discuss the relationship between total stress and effective stress in the UU test. Does anyone know how they’re related?
I think total stress includes pore water pressure, while effective stress is what the soil skeleton can actually support.
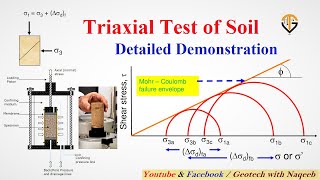
Exactly right! In the context of the UU test, the total stress at failure is given by σ1 = σ3 + Δσf, where Δσf is the additional axial stress. This crucial relationship is pivotal in understanding soil behavior.
How does this relate to the Mohr’s circle we talk about?
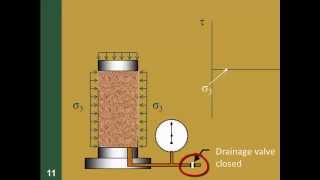
Good question! You can plot Mohr’s circles for total stresses and draw the failure envelope which helps in deducing shear parameters. Remember, in the UU test, we focus more on the Mohr’s circle under constant confining pressure.
Pore Pressure Parameters
Unlock Audio Lesson
Now, let’s focus on the pore pressure parameters involved in UU tests. What do you know about Skempton’s pore pressure parameter B?
Isn't it related to the pore pressure developed during undrained conditions?
Correct! Typically, in soft saturated soils, B is approximately 1. This means it fully contributes to increased pore pressures during loading. Can anyone give me the equation relating pore pressure changes?
u = σ3 + A(σ1 - σ3)?
Exactly! And that parameter A can vary with soil types, which is crucial in practical applications. Just remember, for UU tests, both A and B significantly dictate how pore pressure affects soil strength.
Mohr's Stress Circles
Unlock Audio Lesson
Let's visualize the Mohr’s circles that are created during the UU test. Why is it important to draw these circles?
I think it helps in determining the failure envelope and the shear strength parameters.
Exactly! The Mohr’s circle allows us to determine key parameters c and ϕ visually. When plotting the circles, we find that the horizontal line represents the condition for ϕ=0. Who can recall how this affects our assessment of clay behavior?
It shows that under UU conditions, the soil behaves as if it has no strength cohesion, right?
Spot on! For normally consolidated clay, c is often nearly zero, emphasizing the necessity of these tests in understanding clay properties under undrained loading conditions.
Applications and Importance of the UU Test
Unlock Audio Lesson
Why do you think the UU test is vital in geotechnical engineering?
Because it helps predict how soils will perform under loads without any drainage!
Exactly! It’s fundamental for projects like embankments, foundations, and retaining structures, especially in areas where saturated clay is prevalent.
So, if we have a building on clay, we must know how it behaves under UU conditions?
Correct again! That’s why these tests are not just theoretical; they help us make practical decisions about safety and design. Excellent participation today, everyone!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
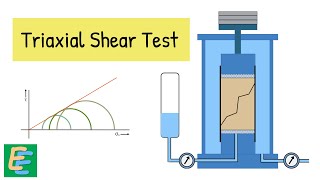
In triaxial testing, the Unconsolidated-undrained test (UU test) evaluates soil behavior under conditions where both consolidation and drainage are not permitted. This test identifies the strength of saturated clays under a constant confining pressure and significant axial loading, crucial for geotechnical engineering applications.
Detailed
Unconsolidated-undrained test (UU test) Overview
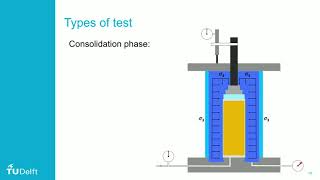
The Unconsolidated-undrained (UU) test is a vital method in geotechnical engineering, particularly for analyzing the stability of saturated fine-grained soils such as clay. The test is performed using triaxial apparatus, which confines soil samples within a rubber membrane inside a chamber. During the UU test, an isotropic confining pressure (σ3) is applied, along with an additional axial stress (Δσ) to provoke failure (at Δσ = Δσf).
In this test, drainage is not permitted, which signifies that pore water pressure may significantly influence the results. The UU test leads to effective stress equations where both principal total and effective stresses are dependent on the applied axial stress and pore pressures. Notably, the total stress Mohr's circle can be plotted, with the shear strength for saturated clays showing a horizontal tangent (ϕ=0 condition). This classifies the UU test as suited for evaluating undisturbed saturated soils, helping infer the shear strength parameters crucial for effective soil stability forecasts.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding the UU Test
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For unconsolidated-undrained triaxial tests
Major principal total stress=σ3=Δσf=σ1
Minor principal total stress =σ3
The total stress Mohr’s circle at failure can now be drawn, as shown in figure. For saturated clays, the value of σ1−σ3=Δσf is a constant, irrespective of the chamber confining pressure, σ3. The tangent to these Mohr’s circles will be a horizontal line, called the ϕ=0 condition.
Detailed Explanation
In the unconsolidated-undrained (UU) test, soil samples are subjected to axial stress without allowing any drainage of pore water. This means that the volume of water in the soil remains unchanged while the stress is applied. The key point here is that the major principal total stress, denoted by σ1, is equal to the confining pressure (σ3) plus the change in stress (Δσf). In simpler terms, when we measure the stress just before the sample fails, this principle helps us determine how strong or stable the soil is under these conditions. The minor principal total stress remains equal to the confining pressure (σ3) during this test. The result from these tests can be illustrated using a Mohr's circle, which graphically represents the stresses acting on the soil sample during failure.
Examples & Analogies
Think of a balloon filled with water. When you squeeze the balloon (applying stress), the water inside exerts pressure outwards. If you keep squeezing without allowing any water to escape (like in the UU test), the pressure can reach a point where the balloon bursts. Similarly, in the UU test, the soil can only hold so much stress without allowing water to drain. Just like the balloon's limit before it pops, the soil also has a point of failure that we can study using the UU test.
Shear Stress in the UU Test
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The shear stress for this condition is
Where
B=Skempton′s pore pressure parameter
Similarly, the pore pressure ud is the result of added axial stress, Δσ, so
ud=A Δσ
Where
A=Skempton′s pore pressure parameter
However,
Δσ=σ1−σ3
Combining equations gives
tu=ua+ud=Bσ3+Aσ1−σ3
The pore water pressure parameter B in soft saturated soils is 1, so
tu=σ3+A(σ1−σ3).
Detailed Explanation
In the UU test, we also consider the shear stress acting on the soil. Shear stress can be understood as the stress that causes layers of soil to slide over each other. The equations provided help calculate the pore pressures within the soil due to applied stresses. The Skempton's pore pressure parameters, A and B, quantify the relationship between the applied stress and the pore water pressure developed within the soil. In particular, A relates the added axial stress to pore pressure, while B relates the confining pressure to pore water pressure. When the pore water pressure parameter B equals 1, it indicates that the soil is fully saturated, leading to a straightforward formula that connects confining stress and the resulting pore water pressure.
Examples & Analogies
Imagine a wet sponge. When you press down on it (adding axial stress), water is forced out, creating pressure inside. The equations are like rules that help us calculate how much water pressure builds up based on how hard we press the sponge. In the UU test, we are analyzing how the pressures within the 'sponge' of soil behave as we change the pressure on the outside. Understanding this helps engineers predict how the soil will react under different conditions.
Pore Pressure at Failure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The value of the pore water pressure parameter A at failure will vary with the type of soil. Following is a general range of the values of A at failure for various types of clayey soil encountered in nature.
Detailed Explanation
When conducting the UU test, the soil type affects the pore pressure parameter A, which plays a significant role in determining the stability and behavior of soil during failure. Different types of clay soils will exhibit varying characteristics with respect to how quickly they respond to stress and how much pore pressure they generate when stressed. This variability is essential for engineers to consider so that they can accurately assess the strength and failure conditions of the soils they are working with.
Examples & Analogies
Think of different kinds of clay you might play with. Some clay is very wet and gooey, making it super easy to mold, while other kinds are dry and stiff, requiring more effort to shape. Similarly, when we apply pressure to different soils, how they respond varies dramatically based on their moisture and consistency. For instance, a wet clay might generate pressure quicker, affecting how it holds together under stress. Understanding these differences in response helps engineers design safer foundations by choosing the right materials for the job.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
UU Test: A method to assess soil behavior under undrained conditions.
-
Pore Pressure: Pressure exerted by fluids in soil and its impact on effective stress.
-
Mohr's Circle: Visual tool for understanding stress states and determining failure conditions.
-
Effective Stress: Critical concept indicating the stress carried by solid soil particles.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A construction project on saturated clay foundation needs to determine if it can support structural loads—this is where the UU test is crucial.
-
A geotechnical engineer uses results from a UU test to design foundations for a new bridge over soft soil, ensuring stability against potential pore pressure increases.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
For clay that's wet, UU's the bet, no drainage in the set!
📖 Fascinating Stories
-
Imagine an engineer on a rainy day assessing soil strength. The rain creates excess pore pressure, and they need to know if their structure will withstand it—that's why they perform a UU test!
🧠 Other Memory Gems
-
UUDS - Unconsolidated Undrained Shear: Remember the key steps in the UU test!
🎯 Super Acronyms
PSTA - Pore Stress, Total Stress, Axial load - keys to remember for effective stress analysis.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: UU test
Definition:
Unconsolidated-undrained test; a triaxial test to evaluate the shear strength of saturated soils without drainage.
-
Term: Pore Pressure
Definition:
The pressure exerted by fluids within the soil's pores which influences effective stress and soil behavior.
-
Term: Mohr's Circle
Definition:
A graphical representation of the states of stress at a point, helping visualize shear and normal stress relationships.
-
Term: Effective Stress
Definition:
The stress carried by soil skeleton excluding pore pressure, crucial for understanding soil strength.