Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Hydrostatic Force
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're diving into hydrostatic force. Letβs start by understanding what it is. Can anyone tell me what hydrostatic means?
I think it has something to do with liquids?
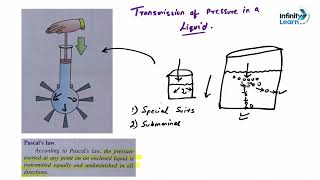
Exactly! Hydrostatic refers to fluids at rest. Hydrostatic force is the force that liquids exert on a submerged surface. Can anyone guess why it changes with depth?
Because thereβs more liquid above, right?
Great observation! The weight of the liquid above increases pressure with depth, which is key to understanding hydrostatic force.
Calculating Hydrostatic Force
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
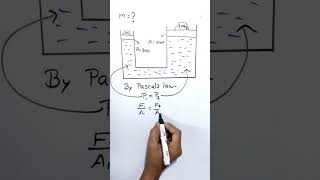
Now letβs learn how we can calculate this force. The formula is $ F = P \times A $. But first, we need the pressure $ P $. Who remembers how to calculate pressure?
Isnβt it $ P = \rho g h $? I remember it from our previous lessons!
Exactly! So letβs say we have a vertical rectangular surface immersed in water. If the density of water is 1000 kg/mΒ³, how would we find the pressure at a depth of 2 meters?
We would plug it into the equation: $ P = 1000 \times 9.8 \times 2 $!
Exactly! And once you have the pressure, you can multiply it by the area to find the hydrostatic force.
Example Problem on Hydrostatic Force Calculation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's work through an example together. If we have a rectangular surface submerged at a depth of 3 meters with an area of 10 mΒ², what would be the hydrostatic force?
First, we calculate the pressure. That would be $ P = 1000 \times 9.8 \times 3 $.
Correct! What do we get for $ P $?
$ 29400 $ Pa.
And now we use the area to find the force. What is $ F $?
$ F = 29400 \times 10 = 294000 $ N.
Fantastic! Thatβs the hydrostatic force on that surface.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Hydrostatic force is the force exerted by the weight of a liquid acting upon a surface that is submerged in it. This force varies across the surface depending on the pressure at different depths, which is calculated by integrating the pressure over the surface area of the object.
Detailed
Hydrostatic Force
Hydrostatic force is the force exerted by a liquid at rest on a surface submerged in it. This force results from the pressure of the liquid, which changes with depth due to the weight of the liquid above. The pressure at a point in the liquid can be calculated using the formula:
$$ P = \rho g h $$
Where:
- $ P $ is the pressure in pascals (Pa),
- $ \rho $ is the density of the liquid in kg/mΒ³,
- $ g $ is the acceleration due to gravity (9.8 m/sΒ²), and
- $ h $ is the depth of the liquid above the point of measurement in meters.
The hydrostatic force ($ F $) on a submerged surface can be calculated using the formula:
$$ F = P \times A $$
Where:
- $ F $ is the hydrostatic force in newtons (N),
- $ P $ is the pressure at the point, and
- $ A $ is the area of the surface.
This section emphasizes the significance of understanding how hydrostatic force operates, particularly in engineering applications like underwater structures, dam construction, and fluid mechanics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Hydrostatic Force on a Surface
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The hydrostatic force on a surface submerged in a liquid is the force exerted by the liquid on that surface. It is calculated by considering the pressure at each point along the surface and integrating this pressure over the entire surface.
Detailed Explanation
Hydrostatic force refers to the total force exerted by a fluid at rest on a surface that is submerged in it. This force comes from the liquidβs weight and acts perpendicular to the surface. To find this force, we need to calculate the pressure acting at each point along the submerged surface. Pressure varies with depth, which means different points on the surface will experience different force levels. By integrating the pressure over the entire surface area, we can find the total hydrostatic force acting on that surface.
Examples & Analogies
Imagine a thick glass wall of an aquarium that is filled with water. The deeper you go down the wall, the more pressure there is from the water above. If you were to measure the force that the water exerts on that wall, you would see that the force increases the deeper you measure, due to the increasing pressure of the water above. The overall force pushing on that wall results from the sum of all these individual pressures at different depths.
Formula for Hydrostatic Force
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The formula for the hydrostatic force is: F=PΓA Where: β F = Hydrostatic force (N) β P = Pressure at the point β A = Area of the surface
Detailed Explanation
The formula for hydrostatic force is straightforward: it states that the hydrostatic force (F) is equal to the pressure (P) multiplied by the area (A) of the surface that is submerged in the liquid. This means that to calculate the total force exerted by the liquid on the surface, we first need to determine the pressure at the surface, which varies based on depth. Once we have that pressure, we simply multiply it by the area of the surface to get the total hydrostatic force.
Examples & Analogies
Think of a large swimming pool with a flat bottom. If you want to know how much force the water is exerting on the bottom of the pool, you would need to know the pressure at a certain depth and the size of that bottom area. If the pressure at that depth is, say, 2000 Pascals and the area of the bottom is 50 square meters, then the hydrostatic force on the bottom is: 2000 Pa Γ 50 mΒ² = 100,000 N. This is the total force pushing up from the water, making the pool bottom feel heavy!
Example: Calculating Hydrostatic Force on a Vertical Surface
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If a vertical rectangular surface is submerged in water, the hydrostatic force on the surface can be calculated by finding the pressure at different points and integrating them.
Detailed Explanation
To calculate the hydrostatic force on a vertical rectangular surface submerged in water, you need to assess the varying pressure at different depths along the surface. Since pressure increases with depth, the force calculated at the bottom of the surface will be greater than at the top. By integrating the pressure across the entire surface β taking into account the depth of each point on the rectangle β you determine the total hydrostatic force. This might involve using calculus to sum up all the infinitesimal contributions to the force.
Examples & Analogies
Picture a large dam with a huge vertical wall. The water pressure at the bottom of the dam wall is much greater than at the top because there is a greater column of water above it. Engineers designing the dam must be able to calculate the total force pushing against the wall at various heights to ensure it can withstand pressure without collapsing. The process of adding up these pressures over the height of the wall is similar to how one would add slices of a cake to figure out the total height of the cake.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydrostatic force is dependent on the pressure exerted by the liquid, which varies with depth.
-
Pressure is calculated using the formula $ P = \rho g h $.
-
The hydrostatic force on a submerged surface can be calculated using $ F = P \times A $.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If a rectangular surface is submerged at a depth of 4 meters in water, what is the hydrostatic force if its area is 5 mΒ²?
-
A vertical gate in a dam measures 3 m by 2 m and is submerged in water. How do we find the hydrostatic force acting on it?
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Pressure is sure, the deeper you go, hydrostatic force will surely grow.
π Fascinating Stories
-
Imagine being underwater. As you go deeper, you feel more weight pushing down on you. Thatβs hydrostatic force increasing!
π§ Other Memory Gems
-
PAM: Pressure = Area Γ Magnitude of hydrostatic force.
π― Super Acronyms
HFS
- Hydrostatic Force = Height Γ Fluid Density Γ Surface Area.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatic Force
Definition:
The force exerted by a liquid at rest on a submerged surface.
-
Term: Pressure
Definition:
The force applied perpendicular to the surface of an object per unit area.
-
Term: Depth
Definition:
The vertical distance below the surface of the liquid.
-
Term: Area
Definition:
The measure of the extent of a two-dimensional surface.